diff options
298 files changed, 8948 insertions, 721 deletions
diff --git a/FSF-2020/approximations-and-optimizations/Critical Points/example.py b/FSF-2020/approximations-and-optimizations/Critical Points/example.py deleted file mode 100644 index 3a41be7..0000000 --- a/FSF-2020/approximations-and-optimizations/Critical Points/example.py +++ /dev/null @@ -1,32 +0,0 @@ -from manimlib.imports import* - -class ExampleAnimation(ThreeDScene): - def construct(self): - axes = ThreeDAxes() - - f_text = TextMobject("$f(x,y) = (y-x)(1-2x-3y)$").to_corner(UL) - d = Dot(np.array([0,0,0]), color = '#800000') #---- Critical Point - d_text = TextMobject("$(0.2,0.2)$",color = '#DC143C').scale(0.5).shift(0.2*UP) #----x = 0.2, y = 0.2 - r_text=TextMobject("Critical Point",color = '#00FFFF').shift(0.3*DOWN).scale(0.6) - - #----f(x,y) = (y-x)(1-2x-3y) - f = ParametricSurface( - lambda u, v: np.array([ - u, - v, - (v-u)*(1-2*u-3*v) - ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [PURPLE_D, PURPLE_E], - resolution=(20, 20)).scale(1) - - self.set_camera_orientation(phi = 75 * DEGREES) - self.begin_ambient_camera_rotation(rate=0.5) - - self.add_fixed_in_frame_mobjects(f_text) - self.wait(1) - self.add(axes) - self.play(Write(f),Write(d)) - self.wait(1) - self.add_fixed_in_frame_mobjects(d_text) - self.wait(1) - self.add_fixed_in_frame_mobjects(r_text) - self.wait(3) diff --git a/FSF-2020/approximations-and-optimizations/Critical Points/motivation.py b/FSF-2020/approximations-and-optimizations/Critical Points/motivation.py deleted file mode 100644 index 27354ef..0000000 --- a/FSF-2020/approximations-and-optimizations/Critical Points/motivation.py +++ /dev/null @@ -1,30 +0,0 @@ -from manimlib.imports import* - -class MotivationAnimation(Scene): - def construct(self): - - r = Rectangle(height = 7,breadth = 2,color = BLUE, fill_opacity = 0.3).scale(0.6) #----metal strip - b = Brace(r,UP) - r_text = TextMobject("$x$ metres",color = YELLOW).shift(3*UP) - m_text = TextMobject("Metal Strip").shift(3*DOWN) - a = Arc(radius=2).rotate(1).shift(LEFT+0.5*UP) - a2 = Arc(radius=2).rotate(5).shift(0.7*LEFT+0.9*UP).scale(0.2) - START = [1,0,0] - END = [0,3,0] - l = Line(START,END,color = RED).shift(0.9*DOWN) - a2_text = TextMobject("$\\theta$",color = PINK).shift(1.6*UP+0.4*RIGHT) - - group1 = VGroup(r_text,b,a,l,a2,a2_text) - f_text = TextMobject("$A = f(x,\\theta)$").shift(2*DOWN) - - ring = Annulus(inner_radius = 0.7, outer_radius = 1, color = BLUE) #--bent metal strip - - self.play(Write(r)) - self.wait(1) - self.play(ShowCreation(m_text)) - self.wait(1) - self.play(Write(group1)) - self.wait(2) - self.play(FadeOut(group1)) - self.wait(1) - self.play(ReplacementTransform(r,ring),ShowCreation(f_text)) diff --git a/FSF-2020/approximations-and-optimizations/Critical Points/theorem.py b/FSF-2020/approximations-and-optimizations/Critical Points/theorem.py deleted file mode 100644 index 7c82aa9..0000000 --- a/FSF-2020/approximations-and-optimizations/Critical Points/theorem.py +++ /dev/null @@ -1,55 +0,0 @@ -from manimlib.imports import* - -class TheoremAnimation(ThreeDScene): - def construct(self): - - axes = ThreeDAxes() - - #----parabola: x**2+y**2 - parabola1 = ParametricSurface( - lambda u, v: np.array([ - u, - v, - u**2+v**2 - ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [TEAL_E], - resolution = (20, 20)).scale(1) - - #----parabola: -x**2-y**2 - parabola2 = ParametricSurface( - lambda u, v: np.array([ - u, - v, - -u**2-v**2 - ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [PURPLE_E,PURPLE_E], - resolution = (20, 20)).scale(1) - - self.set_camera_orientation(phi = 75 * DEGREES) - self.begin_ambient_camera_rotation(rate = 0.4) - - d = Dot(np.array([0,0,0]), color = '#800000') #---- critical point - r = Rectangle(fill_color = '#C0C0C0',fill_opacity = 0.3).move_to(ORIGIN) #----tangent plane - - parabola1_text = TextMobject("Maximum with horizontal tangent plane").scale(0.7).to_corner(UL) - - parabola2_text = TextMobject("Minimum with horizontal tangent plane").scale(0.7).to_corner(UL) - - self.add(axes) - self.add_fixed_in_frame_mobjects(parabola2_text) - self.wait(1) - self.play(Write(parabola1)) - self.wait(1) - self.play(ShowCreation(d)) - self.wait(1) - self.play(ShowCreation(r)) - self.wait(2) - self.play(FadeOut(parabola2_text),FadeOut(parabola1),FadeOut(r),FadeOut(d)) - - self.wait(1) - self.add_fixed_in_frame_mobjects(parabola1_text) - self.wait(1) - self.play(Write(parabola2)) - self.wait(1) - self.play(ShowCreation(d)) - self.wait(1) - self.play(ShowCreation(r)) - self.wait(2) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/README.md b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/README.md new file mode 100644 index 0000000..857d298 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/README.md @@ -0,0 +1,38 @@ +<h1><div align=”center”><b>SubTopic: Critical Points</b></h1></div> +<br/></br> + +<tab>file1_Critical_Point_of_a_function + + +<br/></br> +<br/></br> + +<tab>file2_Traces_and_Tangent + + +<br/></br> +<br/></br> + +<tab>file3_Tangent_plane_at_extrema_of_a_function + + +<br/></br> +<br/></br> + +<tab>file4_Relative_Maximum_and_Relative_Minimum + + +<br/></br> +<br/></br> + +<tab>file5_Saddle_Point + + +<br/></br> +<br/></br> + +<tab>file6_f(x,y)=(y-x)(1-2x-3y) + +%3D(y-x)(1-2x-3y).gif?raw=true) +<br/></br> +<br/></br> diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file1_Critical_Point_of_a_function.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file1_Critical_Point_of_a_function.gif Binary files differnew file mode 100644 index 0000000..ca3989c --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file1_Critical_Point_of_a_function.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file1_Critical_Point_of_a_function.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file1_Critical_Point_of_a_function.py new file mode 100644 index 0000000..e8cb08d --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file1_Critical_Point_of_a_function.py @@ -0,0 +1,77 @@ +from manimlib.imports import* +import math as m + +#---- case 1: parial derivatives exist at critical point of the function +class firstScene(ThreeDScene): + def construct(self): + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.5,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5) #---- y axis + + #---- f(x,y) = e^(-10x^2-10y^2) + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + m.exp(-10*u**2-10*v**2) + ]),u_min = -1, u_max = 1, v_min = -1, v_max = 1, checkerboard_colors = [TEAL_E,TEAL_D,TEAL_C,TEAL_B]).fade(0.6).scale(3.5).shift([0,0,1.5]) + + l1 = Line([0,0,3.75],[0,0,0],color = '#800000') + + d = Dot([0,0,3.75],color = '#800000') #---- critical point + + d_text = TextMobject("$\\frac{\\partial f}{\\partial x}=\\frac{\\partial f}{\\partial y} = 0$").scale(0.8).to_corner(UL) + + f_text = TextMobject("Critical Point ",color = YELLOW).shift(3.4*UP).scale(0.5) + + self.set_camera_orientation(phi = 45*DEGREES, theta = 40*DEGREES) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.add_fixed_in_frame_mobjects(d_text) + self.begin_ambient_camera_rotation(rate = 0.2) + self.play(Write(surface)) + self.wait(1) + self.play(Write(l1)) + self.play(Write(d)) + self.wait(1) + self.add_fixed_in_frame_mobjects(f_text) + self.wait(3) + self.play(FadeOut(f_text),FadeOut(surface),FadeOut(axes),FadeOut(d_text),FadeOut(d),FadeOut(l1),FadeOut(label_x),FadeOut(label_y)) + + +#---- case 2: parial derivatives do not exist at critical point of the function +class secondScene(ThreeDScene): + def construct(self): + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.5,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5) #---- y axis + + #---- g(x,y)= |x|+|y| + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + abs(u)+abs(v) + ]),u_min = -1.5, u_max = 1.5, v_min = -1.5, v_max = 1.5, checkerboard_colors = [TEAL_E,TEAL_D,TEAL_C,TEAL_B]) + + d2 = Dot([0,0,0],color = '#800000') #---- critical point + + d2_text = TextMobject("$\\frac{\\partial f}{\\partial x}$ and/or $\\frac{\\partial f}{\\partial y}$ does not exist").scale(0.7).to_corner(UL) + + g_text = TextMobject("Critical Point",color = YELLOW).shift(1.2*RIGHT).scale(0.6) + + self.set_camera_orientation(phi = 60*DEGREES, theta = 40*DEGREES) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.add_fixed_in_frame_mobjects(d2_text) + self.begin_ambient_camera_rotation(rate = 0.2) + self.wait(1) + self.play(Write(surface2)) + self.wait(1) + self.play(Write(d2)) + self.wait(1) + self.add_fixed_in_frame_mobjects(g_text) + self.wait(2) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file2_Traces_and_Tangent.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file2_Traces_and_Tangent.gif Binary files differnew file mode 100644 index 0000000..84acf2e --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file2_Traces_and_Tangent.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file2_Traces_and_Tangent.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file2_Traces_and_Tangent.py new file mode 100644 index 0000000..4b020e1 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file2_Traces_and_Tangent.py @@ -0,0 +1,88 @@ +from manimlib.imports import* +import math as m + +#---- tangent to the trace with x constant +class firstScene(ThreeDScene): + def construct(self): + + axes = ThreeDAxes().scale(1) + label_x = TextMobject("$x$").shift([5.8,-0.5,0]) + label_y = TextMobject("$y$").shift([-0.5,-5.6,0]).rotate(-4.5) + + #---- graph of f(x,y) = -x^2-y^2 + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -u**2-v**2 + ]),u_min=-1,u_max=1, v_min=-1,v_max=1,checkerboard_colors=[PURPLE_C,PURPLE_D,PURPLE_E,PURPLE_B]).scale(1.5).shift([0,0,2]).rotate(0.2) + + #---- curve(trace) along y axis + curve = ParametricSurface( + lambda u, v: np.array([ + u*0.4, + v, + -v**2 + ]),v_min =-1 , v_max =1 , u_min = -0.1, u_max = 0.1).scale(1.6).shift([0.02,0.1,2.3]).set_color("#800000").rotate(0.1) + + d = Dot(color =YELLOW).shift([-0.05,-0.2,2.3]) #---- critical point + + x_text = TextMobject("Tangent to the trace with $x$ constant at critical point").shift(3*RIGHT+2*UP).scale(0.5).to_corner(UL) + + tangent_line = Line([-0.05,-1.5,2.3],[-0.05,1.5,2.3],color = '#228B22') + + self.add(axes) + self.set_camera_orientation(phi = 40 * DEGREES, theta = 55 * DEGREES) + self.begin_ambient_camera_rotation(rate = 0.1) + self.add(label_x) + self.add(label_y) + self.play(Write(surface)) + self.add_fixed_in_frame_mobjects(x_text) + self.add(curve) + self.wait(1) + self.play(Write(tangent_line),Write(d)) + self.wait(1) + + + +#---- tangent to the trace with y constant +class secondScene(ThreeDScene): + def construct(self): + + axes = ThreeDAxes().scale(1) + label_x = TextMobject("$x$").shift([5.8,-0.5,0]) + label_y = TextMobject("$y$").shift([-0.5,-5.6,0]).rotate(-4.5) + + #---- graph of f(x,y) = -x^2-y^2 + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -u**2-v**2 + ]),u_min = -1, u_max = 1, v_min = -1, v_max = 1, checkerboard_colors = [PURPLE_B,PURPLE_C,PURPLE_D,PURPLE_E]).scale(1.5).shift([0,0,2]).rotate(0.2) + + #---- curve(trace) along x axis + curve = ParametricSurface( + lambda u, v: np.array([ + u, + v*0.4, + -u**2 + ]),v_min = -0.1, v_max = 0.1, u_min = -1, u_max = 1).scale(1.6).shift([0.07,0.1,2.3]).set_color("#800000") + + d = Dot(color = YELLOW).shift([0,-0.2,2.3]) #---- critical point + + tangent_line = Line(color = '#228B22').scale(1).shift([0,-0.2,2.3]).rotate(m.radians(190),LEFT) + + y_text = TextMobject("Tangent to the trace with $y$ constant at critical point").shift(3*RIGHT+2*UP).scale(0.5).to_corner(UL) + + self.add(axes) + self.set_camera_orientation(phi = 40 * DEGREES, theta = 55 * DEGREES) + self.add(label_x) + self.add(label_y) + self.begin_ambient_camera_rotation(rate = 0.1) + self.play(Write(surface)) + self.add_fixed_in_frame_mobjects(y_text) + self.add(curve) + self.wait(1.5) + self.play(Write(tangent_line),Write(d)) + self.wait(0.5) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file3_Tangent_plane_at_extrema_of_a_function.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file3_Tangent_plane_at_extrema_of_a_function.gif Binary files differnew file mode 100644 index 0000000..14fb318 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file3_Tangent_plane_at_extrema_of_a_function.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file3_Tangent_plane_at_extrema_of_a_function.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file3_Tangent_plane_at_extrema_of_a_function.py new file mode 100644 index 0000000..e674113 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file3_Tangent_plane_at_extrema_of_a_function.py @@ -0,0 +1,73 @@ +from manimlib.imports import* + +#---- tangent plane to minima of the function +class firstScene(ThreeDScene): + def construct(self): + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.5,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5) #---- y axis + + #---- parabola: f(x,y) = x**2 + y**2 + parabola = ParametricSurface( + lambda u, v: np.array([ + u, + v, + u**2+v**2 + ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [GREEN_E,GREEN_D,GREEN_C,GREEN_B], resolution = (20, 20)).scale(1) + + d = Dot(np.array([0,0,0]), color = '#800000') # ---- critical point + + tangent_plane = Rectangle(fill_color = '#C0C0C0', fill_opacity = 0.3).move_to(ORIGIN).fade(0.7) # ----tangent plane + + parabola_text = TextMobject("Minimum with horizontal tangent plane").scale(0.7).to_corner(UL) + + self.set_camera_orientation(phi = 75 * DEGREES, theta = 45 * DEGREES) + self.begin_ambient_camera_rotation(rate = 0.2) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.add_fixed_in_frame_mobjects(parabola_text) + self.wait(1) + self.play(Write(parabola)) + self.play(ShowCreation(d)) + self.wait(1) + self.play(ShowCreation(tangent_plane)) + self.wait(2) + self.play(FadeOut(parabola_text),FadeOut(parabola),FadeOut(tangent_plane),FadeOut(d),FadeOut(label_x),FadeOut(label_y),FadeOut(axes)) + + +#---- tangent plane to maxima of the function +class secondScene(ThreeDScene): + def construct(self): + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.5,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5) #---- y axis + + #----parabola: g(x,y) = -x**2-y**2 + parabola = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -u**2-v**2 + ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [BLUE_E,BLUE_D,BLUE_C,BLUE_B], resolution = (20, 20)).scale(1) + + d = Dot(np.array([0,0,0]), color = '#800000') #---- critical point + + tangent_plane = Rectangle(fill_color = '#C0C0C0',fill_opacity = 0.3).move_to(ORIGIN).fade(0.7) #---- tangent plane + + parabola_text = TextMobject("Maximum with horizontal tangent plane").scale(0.7).to_corner(UL) + + self.set_camera_orientation(phi = 75 * DEGREES, theta = 45 * DEGREES) + self.begin_ambient_camera_rotation(rate = 0.2) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.add_fixed_in_frame_mobjects(parabola_text) + self.wait(1) + self.play(Write(parabola)) + self.play(ShowCreation(d)) + self.wait(1) + self.play(ShowCreation(tangent_plane)) + self.wait(2) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file4_Relative_Maximum_and_Relative_Minimum.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file4_Relative_Maximum_and_Relative_Minimum.gif Binary files differnew file mode 100644 index 0000000..6b93359 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file4_Relative_Maximum_and_Relative_Minimum.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file4_Relative_Maximum_and_Relative_Minimum.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file4_Relative_Maximum_and_Relative_Minimum.py new file mode 100644 index 0000000..3bd810d --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file4_Relative_Maximum_and_Relative_Minimum.py @@ -0,0 +1,51 @@ +from manimlib.imports import* +import math as m + +#---- locating extrema of a funtion using critical points +class Extrema(ThreeDScene): + def construct(self): + + h_text = TextMobject("Relative Maximum and Relative Minimum",color = GREEN) + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.3,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.3,5.5,0]).rotate(-4.5) #---- y axis + + #---- f(x,y) = 5(x+y)e^(-x^2-y^2) + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + 5*(u+v)*m.exp(-u**2-v**2) + ]),u_min = -PI, u_max = PI, v_min = -PI, v_max = PI).set_color(TEAL).shift([0,0,0]).fade(0.4) + + d1 = Dot(color = YELLOW).shift([0.5,0.5,3.02]) #---- critical point for maxima + l1 = Line([0.5,0.5,0.1],[0.5,0.5,3],color = YELLOW) + + d2 = Dot(color = YELLOW).shift([-1.15,0,-2.98]) #---- critical point for minima + l2 = Line([-1.15,0,0],[-1.15,0,-2.98],color = YELLOW) + + max_text = TextMobject("Relative Maximum").shift(3.1*UP+1.5*RIGHT).scale(0.5) + min_text = TextMobject("Relative Minimum").shift(3.1*DOWN+1.5*LEFT).scale(0.5) + + self.add_fixed_in_frame_mobjects(h_text) + self.wait(1) + self.wait(1) + self.play(FadeOut(h_text)) + self.wait(1) + self.set_camera_orientation(phi = 100*DEGREES, theta = -40*DEGREES) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.play(Write(surface)) + self.wait(1) + self.play(Write(l1),Write(d1)) + self.add_fixed_in_frame_mobjects(max_text) + self.wait(1) + self.play(Write(l2),Write(d2)) + self.add_fixed_in_frame_mobjects(min_text) + self.wait(1) + self.wait(1) + self.play(FadeOut(l1),FadeOut(d1),FadeOut(l2),FadeOut(d2),FadeOut(max_text),FadeOut(min_text)) + self.begin_ambient_camera_rotation(rate = 0.3) + self.wait(3) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file5_Saddle_Point.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file5_Saddle_Point.gif Binary files differnew file mode 100644 index 0000000..7300f3a --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file5_Saddle_Point.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file5_Saddle_Point.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file5_Saddle_Point.py new file mode 100644 index 0000000..67dbb18 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file5_Saddle_Point.py @@ -0,0 +1,71 @@ +from manimlib.imports import* +import math as m + +#---- saddle point of a function +class SaddlePoint(ThreeDScene): + def construct(self): + + h_text = TextMobject("Saddle Point",color = GREEN) + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.3,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.3,5.5,0]).rotate(-4.5) #---- y axis + + #---- f(x,y) = -x^2-y^2 + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + u**2-v**2 + ]),u_min = -1, u_max = 1, v_min = -1, v_max = 1,checkerboard_colors = [BLUE_B,BLUE_C,BLUE_D,BLUE_E]).shift([0,0,0]).scale(3) + + #---- curve(trace) along y axis + curve_x = ParametricSurface( + lambda u, v: np.array([ + u*0.1, + v, + v**2 + ]),v_min = -1, v_max = 1, u_min = -0.2, u_max = 0.2).shift([0,0,-2]).scale(3.1).set_color("#800000").rotate(m.radians(180),UP) + + x_text = TextMobject("A dip at critical point along x axis").scale(0.5).to_corner(UL) + + #---- curve(trace) along x axis + curve_y = ParametricSurface( + lambda u, v: np.array([ + u, + v*0.1, + -u**2 + ]),v_min = -0.2, v_max = 0.2, u_min = -1, u_max = 1).scale(3).shift([0.1,0,2.2]).set_color("#800000").rotate(m.radians(182),DOWN) + + y_text = TextMobject("A peak at critical point along y axis").scale(0.5).to_corner(UL) + + d = Dot(color = YELLOW).shift([0,-0.22,0]) #---- critical point(saddle point) + + self.add_fixed_in_frame_mobjects(h_text) + self.wait(1) + self.play(FadeOut(h_text)) + self.wait(1) + self.set_camera_orientation(phi = 75*DEGREES, theta = 40*DEGREES) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.play(Write(surface)) + self.wait(1) + self.move_camera(phi = 45*DEGREES, theta = 70*DEGREES) + self.add(curve_y) + self.play(Write(d)) + self.wait(1) + self.add_fixed_in_frame_mobjects(x_text) + self.wait(1) + self.wait(1) + self.play(FadeOut(curve_y),FadeOut(d),FadeOut(x_text)) + self.wait(1) + self.move_camera(phi = 40*DEGREES, theta = 30*DEGREES) + self.add(curve_x) + self.play(Write(d)) + self.wait(1) + self.add_fixed_in_frame_mobjects(y_text) + self.begin_ambient_camera_rotation(rate = 0.3) + self.wait(3) + self.play(FadeOut(curve_x),FadeOut(d),FadeOut(y_text)) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file6_f(x,y)=(y-x)(1-2x-3y).gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file6_f(x,y)=(y-x)(1-2x-3y).gif Binary files differnew file mode 100644 index 0000000..4bc92f8 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file6_f(x,y)=(y-x)(1-2x-3y).gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file6_f(x,y)=(y-x)(1-2x-3y).py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file6_f(x,y)=(y-x)(1-2x-3y).py new file mode 100644 index 0000000..41c3b61 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical-Points/file6_f(x,y)=(y-x)(1-2x-3y).py @@ -0,0 +1,29 @@ +from manimlib.imports import* + +#---- visualization of the function +class ExampleAnimation(ThreeDScene): + def construct(self): + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.5,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5) #---- y axis + + #---- f(x,y) = (y-x)(1-2x-3y) + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + (v-u)*(1-2*u-3*v) + ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [PURPLE_B,PURPLE_C,PURPLE_D, PURPLE_E]).scale(1).fade(0.2).shift([0.2,0.2,0]) + + f_text = TextMobject("$f(x,y) = (y-x)(1-2x-3y)$").to_corner(UL) + + self.set_camera_orientation(phi = 60 * DEGREES, theta = 75 * DEGREES) + self.begin_ambient_camera_rotation(rate=0.1) + self.add_fixed_in_frame_mobjects(f_text) + self.wait(1) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.wait(1) + self.play(Write(f)) + self.wait(4) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/README.md b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/README.md new file mode 100644 index 0000000..05ff51d --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/README.md @@ -0,0 +1,20 @@ +<h1><div align=”center”><b>SubTopic: Lagrange Multipliers</b></h1></div> +<br/></br> + +<tab>file1_Extrema_over_g(x,y)=k + +%3Dk.gif?raw=true) +<br/></br> +<br/></br> + +<tab>file2_Geometric_Proof + + +<br/></br> +<br/></br> + +<tab>file3_Constraints_g_and_h + + +<br/></br> +<br/></br> diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file1_Extrema_over_g(x,y)=k.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file1_Extrema_over_g(x,y)=k.gif Binary files differnew file mode 100644 index 0000000..d423943 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file1_Extrema_over_g(x,y)=k.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file1_Extrema_over_g(x,y)=k.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file1_Extrema_over_g(x,y)=k.py new file mode 100644 index 0000000..a01efb0 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file1_Extrema_over_g(x,y)=k.py @@ -0,0 +1,45 @@ +from manimlib.imports import* +import math as m + +#---- optimizing funtion f(x,y) w.r.t to g(x,y) +class ConstrainedExtrema(ThreeDScene): + def construct(self): + axes = ThreeDAxes().fade(0.4) + label_x = TextMobject("$x$").shift([5.5,-0.5,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5) #---- y axis + + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + u**2+v**2+u**3-v**3 + ]),u_min=-0.5,u_max=0.5, v_min=-0.5,v_max=0.5).scale(5).shift([0,1,2.5]).set_color(TEAL).fade(0.2) + + c = Circle(color='#FF00FF',fill_opacity=0.3).shift([-0.4,0,1.5]).rotate(1.9,UP).scale(0.7) + + minima = Dot(color = '#4169E1').shift([-0.5,0.5,1]).rotate(1.571,UP) + maxima = Dot(color = '#4169E1').shift([0.1,0,2.2]).rotate(1.571,UP) + + max_text = TextMobject("maximum over $g(x,y)=k$",color = '#FFA074').scale(0.6).shift(2.3*UP+2*LEFT) + min_text = TextMobject("minimum over $g(x,y)=k$",color = '#FFA074').shift([2.5,0.5,1]).scale(0.6).shift(0.5*UP) + label_f = TextMobject("$z=f(x,y)$",color=TEAL).scale(0.8).shift(3*UP+3*RIGHT) + label_g = TextMobject("g(x,y)=k",color = PURPLE).scale(0.5).shift(1.5*UP+0.8*LEFT) + + + self.add(axes) + self.add(label_x) + self.add(label_y) + self.set_camera_orientation(phi=75*DEGREES,theta=45*DEGREES) + self.play(Write(surface)) + self.add_fixed_in_frame_mobjects(label_f) + self.wait(2) + self.play(Write(c)) + self.wait(1) + self.add_fixed_in_frame_mobjects(label_g) + self.wait(1) + self.play(Write(maxima)) + self.add_fixed_in_frame_mobjects(max_text) + self.wait(1) + self.play(Write(minima)) + self.add_fixed_in_frame_mobjects(min_text) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file2_Geometric_Proof.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file2_Geometric_Proof.gif Binary files differnew file mode 100644 index 0000000..e028a81 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file2_Geometric_Proof.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file2_Geometric_Proof.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file2_Geometric_Proof.py new file mode 100644 index 0000000..2c1d668 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file2_Geometric_Proof.py @@ -0,0 +1,89 @@ +from manimlib.imports import* + +#---- visualization of geometric proof of Lagrange multiplier +class firstScene(ThreeDScene): + def construct(self): + axes = ThreeDAxes().scale(0.7).rotate(math.radians(180)) + label_x = TextMobject("$x$").shift(4*RIGHT).fade(0.4) #---- x axis + label_y = TextMobject("$y$").shift(3.2*DOWN+0.2*RIGHT).rotate(math.radians(180)).fade(0.4) #---- y axis + + surface = ParametricSurface( + lambda u, v: np.array([ + 1*np.sin(u)*np.cos(v), + 1*np.sin(u)*np.sin(v), + -1*np.sin(u)*np.sin(u)+2 + ]),u_min=0,u_max=PI/2,v_min=0,v_max=2*PI).set_color(GREEN).scale(1).shift([-1.5,-1.5,0]) + + d = Dot([-2,-2.55,0],color = '#800000') + a_df = Arrow(color = '#00FFFF').rotate(-2).shift(3.2*DOWN+2.3*LEFT) #---- f parallel to g + a_dg = Arrow(color = '#FF00FF').scale(0.8).shift(3.2*DOWN+2.3*LEFT).rotate(-2) #---- f parallel to g + + b_dg = Arrow(color = '#00FFFF').rotate(1.1).shift(0.82*LEFT+0.15*UP) #---- f parallel to g + b_df = Arrow(color = '#FF00FF').scale(0.6).rotate(-2).shift(1.43*LEFT+1.1*DOWN) #---- f parallel to g + + + qd = Dot(color = '#800000').shift(1.2*LEFT+0.6*DOWN) + + l1 = Line([-1,-3.1,0],[-4,-3.1,0],color = PINK).rotate(-0.3).fade(0.6) + l2 = Line([-0.9,-2.9,0],[-4,-2.9,0],color = PINK).rotate(-0.3).fade(0.6) + l3= Line([-0.8,-2.7,0],[-4,-2.7,0],color = PINK).rotate(-0.3).fade(0.6) + l4= Line([-0.7,-2.45,0],[-4,-2.45,0],color = PINK).rotate(-0.3).fade(0.6) + l5= Line([-0.6,-2.2,0],[-4,-2.25,0],color = PINK).rotate(-0.3).fade(0.6) + l6 = Line([-0.5,-2,0],[-4,-2,0],color = PINK).rotate(-0.3).fade(0.6) + l7 = Line([-0.4,-1.8,0],[-4,-1.8,0],color = PINK).rotate(-0.3).fade(0.6) + l8 = Line([-0.3,-1.6,0],[-4,-1.6,0],color = PINK).rotate(-0.3).fade(0.6) + l9= Line([-0.2,-1.4,0],[-4,-1.4,0],color = PINK).rotate(-0.3).fade(0.6) + l10= Line([-0.1,-1.2,0],[-4,-1.2,0],color = PINK).rotate(-0.3).fade(0.6) + l11 = Line([-0,-1,0],[-4,-1,0],color = PINK).rotate(-0.3).fade(0.6) + l12 = Line([-0,-0.8,0],[-4,-0.8,0],color = PINK).rotate(-0.3).fade(0.6) + l13= Line([-0,-0.55,0],[-4,-0.55,0],color = PINK).rotate(-0.3).fade(0.6) + l14= Line([-0,-0.35,0],[-4,-0.35,0],color = PINK).rotate(-0.3).fade(0.6) + l15= Line([-0.,-0.15,0],[-4,-0.15,0],color = PINK).rotate(-0.3).fade(0.6) + + rel_text = TextMobject("$\\nabla f = \\lambda \\nabla g$",color = TEAL).shift([3,3.2,0]).scale(0.5) + + f_text = TextMobject("$\\nabla f$",color = '#800000').shift([1,1,0]).scale(0.5) + g_text = TextMobject("$\\nabla g$").shift([1.2,-0.8,0]).scale(0.5) + + p_text= TextMobject("$P$").shift([1.8,2.6,0]).scale(0.5) + + l1_text = TextMobject("$w=$ 17").rotate(math.radians(180)).scale(0.4).shift(2.7*DOWN+4.36*LEFT) + l2_text = TextMobject("$w=$ 16").rotate(math.radians(180)).scale(0.4).shift(2.46*DOWN+4.36*LEFT) + l3_text = TextMobject("$w=$ 15").rotate(math.radians(180)).scale(0.4).shift(2.2*DOWN+4.36*LEFT) + l4_text = TextMobject("$w=$ 14").rotate(math.radians(180)).scale(0.4).shift(1.97*DOWN+4.36*LEFT) + l5_text = TextMobject("$w=$ 13").rotate(math.radians(180)).scale(0.4).shift(1.74*DOWN+4.36*LEFT) + l6_text = TextMobject("$w=$ 12").rotate(math.radians(180)).scale(0.4).shift(1.5*DOWN+4.36*LEFT) + l7_text = TextMobject("$w=$ 11").rotate(math.radians(180)).scale(0.4).shift(1.26*DOWN+4.36*LEFT) + l8_text = TextMobject("$w=$ 10").rotate(math.radians(180)).scale(0.4).shift(1.05*DOWN+4.36*LEFT) + l9_text = TextMobject("$w=$ 9").rotate(math.radians(180)).scale(0.4).shift(0.8*DOWN+4.32*LEFT) + l10_text = TextMobject("$w=$ 8").rotate(math.radians(180)).scale(0.4).shift(0.6*DOWN+4.32*LEFT) + l11_text = TextMobject("$w=$ 7").rotate(math.radians(180)).scale(0.4).shift(0.4*DOWN+4.32*LEFT) + l12_text = TextMobject("$w=$ 6").rotate(math.radians(180)).scale(0.4).shift(0.2*DOWN+4.32*LEFT) + l13_text = TextMobject("$w=$ 5").rotate(math.radians(180)).scale(0.4).shift(-0.02*DOWN+4.32*LEFT) + l14_text = TextMobject("$w=$ 4").rotate(math.radians(180)).scale(0.4).shift(-0.23*DOWN+4.32*LEFT) + l15_text = TextMobject("$w=$ 3").rotate(math.radians(180)).scale(0.4).shift(-0.44*DOWN+4.32*LEFT) + + level_Curve = VGroup(l1,l1_text,l2,l2_text,l3,l3_text,l4,l4_text,l5,l5_text,l6,l6_text,l7,l7_text,l8,l8_text,l9,l9_text,l10,l10_text,l11,l11_text,l12,l12_text,l13,l13_text,l14,l14_text,l15,l15_text) + + self.set_camera_orientation(phi=0 * DEGREES, theta = 90*DEGREES) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.wait(1) + self.add(surface) + self.wait(1) + self.play(ShowCreation(level_Curve)) + self.wait(1) + self.play(ShowCreation(a_df),ShowCreation(a_dg),Write(d)) + self.wait(1) + self.add_fixed_in_frame_mobjects(rel_text) + self.add_fixed_in_frame_mobjects(p_text) + self.wait(1) + self.play(Write(qd)) + self.wait(1) + self.play(ShowCreation(b_df)) + self.add_fixed_in_frame_mobjects(f_text) + self.wait(1) + self.play(ShowCreation(b_dg)) + self.add_fixed_in_frame_mobjects(g_text) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file3_Constraints_g_and_h.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file3_Constraints_g_and_h.gif Binary files differnew file mode 100644 index 0000000..0da30ad --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file3_Constraints_g_and_h.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file3_Constraints_g_and_h.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file3_Constraints_g_and_h.py new file mode 100644 index 0000000..742d6b5 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Lagrange-Multipliers/file3_Constraints_g_and_h.py @@ -0,0 +1,41 @@ +from manimlib.imports import* +import math as m + +class firstScene(ThreeDScene): + def construct(self): + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.5,0]).fade(0.4) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5).fade(0.4) #---- y axis + + #---- constraint g(x,y) + cylinder = ParametricSurface( + lambda u, v: np.array([ + np.cos(TAU * u), + np.sin(TAU * u), + 2 * (v) + ]),checkerboard_colors=[YELLOW_C,YELLOW_D,YELLOW_E]).rotate(m.radians(-40),RIGHT).shift([0.5,0.5,0]).scale(0.8) + + #---- constraint h(x,y) + plane = ParametricSurface( + lambda u, v: np.array([ + u, + v, + u+v + ]),checkerboard_colors=[TEAL_C,TEAL_D,TEAL_E]).shift([0,0,0]).rotate(m.radians(-40),RIGHT).scale(2).fade(0.3) + + figure = VGroup(cylinder,plane).rotate(m.radians(-45),DOWN).scale(1.5) + + self.set_camera_orientation(phi=65*DEGREES,theta=45*DEGREES) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.wait(1) + self.play(Write(cylinder)) + self.play(Write(plane)) + self.wait(1) + self.begin_ambient_camera_rotation(rate=0.4) + self.wait(1) + self.wait(1) + self.play(FadeOut(label_x),FadeOut(label_y)) + self.wait(1) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical_Points_mcq_questions.pdf b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Critical_Points_mcq_questions.pdf Binary files differindex 25c4e4d..25c4e4d 100644 --- a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Critical_Points_mcq_questions.pdf +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Critical_Points_mcq_questions.pdf diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Lagrange_Multipliers_mcq_questions.pdf b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Lagrange_Multipliers_mcq_questions.pdf Binary files differnew file mode 100644 index 0000000..3ba7d1c --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Lagrange_Multipliers_mcq_questions.pdf diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Tangent_Plane_Approximations_mcq_questions.pdf b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Tangent_Plane_Approximations_mcq_questions.pdf Binary files differnew file mode 100644 index 0000000..2a77b15 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Tangent_Plane_Approximations_mcq_questions.pdf diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The_Second_Derivative_Test_MCQ.pdf b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/The_Second_Derivative_Test_mcq_questions.pdf Binary files differindex ca60cbf..ca60cbf 100644 --- a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The_Second_Derivative_Test_MCQ.pdf +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/The_Second_Derivative_Test_mcq_questions.pdf diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Total_Differential_mcq_questions.pdf b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Total_Differential_mcq_questions.pdf Binary files differnew file mode 100644 index 0000000..b1a679d --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/MCQ-Questions/Total_Differential_mcq_questions.pdf diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/README.md b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/README.md new file mode 100644 index 0000000..2a274d0 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/README.md @@ -0,0 +1,26 @@ +<h1><div align=”center”><b>SubTopic: Tangent Plane Approximations</b></h1></div> +<br/></br> + +<tab>file1_Tangent_Plane + + +<br/></br> +<br/></br> + +<tab>file2_Tangent_plane_approximation_visualization + + +<br/></br> +<br/></br> + +<tab>file3_Non_Differentiable_Function + + +<br/></br> +<br/></br> + +<tab>file4_Tangent_plane_at_extrema_and_saddle_point + + +<br/></br> +<br/></br> diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file1_Tangent_Plane.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file1_Tangent_Plane.gif Binary files differnew file mode 100644 index 0000000..2b8bf5f --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file1_Tangent_Plane.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file1_Tangent_Plane.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file1_Tangent_Plane.py new file mode 100644 index 0000000..8efdbd2 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file1_Tangent_Plane.py @@ -0,0 +1,50 @@ +from manimlib.imports import* + +#---- tangent plane is parallel to the surface of the funtion at a point +class tangentplane(ThreeDScene): + def construct(self): + + s1_text=TextMobject("Suppose, the point $(x,y)$ lies on the surface of the function.").scale(0.5).shift(2*UP) + s2_text=TextMobject("When zooming on that point, the surface would appear more and more like a plane.").scale(0.5).shift(1*UP) + s3_text=TextMobject("This plane is called the tangent plane.").scale(0.5) + + #---- graph of function f(x,y) = -x^2-y^2 + + f = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -u**2-v**2 + ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [YELLOW_B,YELLOW_C,YELLOW_D, YELLOW_E]).shift([0,0,0]).scale(1) + + + d = Dot([0,0,0],color = '#800000') #---- critical point + + r = Rectangle(color = PURPLE,fill_opacity=0.2).shift([0.1,0,0]).scale(0.3) #---- tangent plane + + s = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -u**2-v**2 + ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [YELLOW_B,YELLOW_C,YELLOW_D, YELLOW_E]).shift([0,0,0]).scale(3.5) + + d2 = Dot([0,0,2.5],color = '#800000') #---- changing position of critical point + + r2 = Rectangle(color = PURPLE,fill_opacity=0.5).shift([0.1,0,2.5]).scale(0.3) #---- changing position of tangent plane + + self.set_camera_orientation(phi = 50 * DEGREES, theta = 45 * DEGREES) + self.add_fixed_in_frame_mobjects(s1_text) + self.add_fixed_in_frame_mobjects(s2_text) + self.add_fixed_in_frame_mobjects(s3_text) + self.wait(2) + self.play(FadeOut(s1_text)) + self.play(FadeOut(s2_text)) + self.play(FadeOut(s3_text)) + self.wait(1) + self.play(Write(f)) + self.play(Write(d)) + self.play(Write(r)) + self.wait(2) + self.play(ReplacementTransform(f,s),ReplacementTransform(d,d2),ReplacementTransform(r,r2)) + self.wait(2) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file2_Tangent_plane_approximation_visualization.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file2_Tangent_plane_approximation_visualization.gif Binary files differnew file mode 100644 index 0000000..6d5a67a --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file2_Tangent_plane_approximation_visualization.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file2_Tangent_plane_approximation_visualization.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file2_Tangent_plane_approximation_visualization.py new file mode 100644 index 0000000..02576d9 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file2_Tangent_plane_approximation_visualization.py @@ -0,0 +1,85 @@ +from manimlib.imports import* +import math as m + +#---- tangent plane approximation visualization +class ApproximationScene(ThreeDScene): + def construct(self): + + axes = ThreeDAxes().scale(1.2).fade(0.7) + label_x= TextMobject("$x$").shift([5.4,-0.5,0]).fade(0.7) #---- x axis + label_y= TextMobject("$y$").shift([-0.5,5.2,0]).rotate(-4.5).fade(0.7) #---- y axis + + #---- graph of the function + s = ParametricSurface( + lambda u, v: np.array([ + 1.5*np.cos(u)*np.cos(v), + 1.5*np.cos(u)*np.sin(v), + 1.5*np.sin(u) + ]),u_min=0,u_max=PI,v_min=PI,v_max=2*PI,checkerboard_colors=[BLUE_B,BLUE_C,BLUE_D,BLUE_E]).shift([0,1,2.4]).scale(1.3) + + d1 = Dot([0.2,2.01,2.24],color = '#800000').rotate(1.1,LEFT) #---- point(x_0,y_0) + d1_copy = Dot([0.2,2.01,0],color = '#800000') #---- projection of point(x_0,y_0) on x-y plane + + d1_text = TextMobject("$f(x_0,y_0)$",color=ORANGE).scale(0.5).shift([0.2,2.01,2.3]) + d1_copy_text = TextMobject("$(x_0,y_0)$",color=ORANGE).scale(0.5).shift([0.2,2.01,0],4.1*DOWN) + + d2 = Dot([2,2.6,3.5],color = '#800000').rotate(1,LEFT) #---- point(x,y) + d2_copy = Dot([2,2.6,0],color = '#800000') #---- projection of point(x,y) on x-y plane + + d2_text = TextMobject("$f(x,y)$",color=ORANGE).scale(0.5).shift([0.8,1.4,1.5]) + d2_copy_text = TextMobject("$(x,y)$",color=ORANGE).scale(0.5).shift([0.8,1.4,0],2.4*DOWN) + + l1 = Line([0.2,2.01,2.21],[0.2,2.01,0],color= YELLOW).fade(0.2) + l2 = Line([2,2.6,3.4],[2,2.6,0],color= YELLOW).fade(0.2) + + t_plane = Rectangle(color = PURPLE, fill_opacity=0.3).scale(0.6).rotate(m.radians(45),LEFT).shift([1.1,2.5,3.1]) #---- tangent plane + t_text= TextMobject("Tangent Plane",color = PINK).scale(0.5).shift(0.3*RIGHT+2.6*UP).rotate(math.radians(5),LEFT) + + a1 = Line([0.2,2.01,0],[2,2.6,0],color ="#00FF7F") + a_x = Line([0.2,2.01,0],[2,2.01,0],color ="#9400D3") + a_y = Line([0.2,2.01,0],[0.2,2.6,0],color ="#8B4513") + a2 = Line([2,2.01,0],[2,2.6,0]) + a3 = Line([0.2,2.6,0],[2,2.6,0]) + + ax_text = TextMobject("$f_x (x_0 , y_0 )(x – x_0 ) $").scale(0.5).shift(DOWN+0.8*LEFT).rotate(0.4) + ay_text = TextMobject("$ f_y (x_0 , y_0 )(y – y_0 ) $").scale(0.5).shift(0.8*DOWN+2.7*RIGHT).rotate(-0.6) + a1_text = TextMobject("$f_x (x_0 , y_0 )(x – x_0 ) + f_y (x_0 , y_0 )(y – y_0 )$ ").scale(0.4).rotate(0.7).shift(1.7*DOWN+0.6*RIGHT) + + lines = VGroup(a1,a_y,a_x,a2,a3,d1_copy,d2_copy) + + + self.set_camera_orientation(phi = 60 * DEGREES, theta = 55 * DEGREES) + self.wait(1) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.play(Write(s)) + self.wait(1) + self.play(Write(d2)) + self.add_fixed_in_frame_mobjects(d1_text) + self.wait(1) + self.play(Write(t_plane)) + self.add_fixed_in_frame_mobjects(t_text) + self.wait(1) + self.play(Write(d1)) + self.add_fixed_in_frame_mobjects(d2_text) + self.wait(1) + self.play(Write(l1),Write(d1_copy)) + self.add_fixed_in_frame_mobjects(d2_copy_text) + self.wait(1) + self.play(Write(l2),Write(d2_copy)) + self.add_fixed_in_frame_mobjects(d1_copy_text) + self.wait(2) + self.play(FadeOut(d1_text),FadeOut(d1_copy_text),FadeOut(d2_text),FadeOut(d2_copy_text),FadeOut(t_text)) + self.wait(1) + self.play(Write(a1),Write(a_x),Write(a_y),Write(a2),Write(a3)) + self.wait(1) + self.play(FadeOut(s),FadeOut(d1),FadeOut(d2),FadeOut(l1),FadeOut(l2),FadeOut(t_plane),FadeOut(label_x),FadeOut(label_y)) + self.wait(1) + lines.scale(2) + axes.scale(1.5) + self.wait(1) + self.add_fixed_in_frame_mobjects(ax_text) + self.add_fixed_in_frame_mobjects(ay_text) + self.add_fixed_in_frame_mobjects(a1_text) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file3_Non_Differentiable_Function.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file3_Non_Differentiable_Function.gif Binary files differnew file mode 100644 index 0000000..7581a33 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file3_Non_Differentiable_Function.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file3_Non_Differentiable_Function.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file3_Non_Differentiable_Function.py new file mode 100644 index 0000000..79d0948 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file3_Non_Differentiable_Function.py @@ -0,0 +1,47 @@ +from manimlib.imports import* +import math + +#---- tangent plane does not exists for f(x,y): sqrt(x**2+y**2) at origin + +class TangenttoSurface(ThreeDScene): + def construct(self): + axes = ThreeDAxes().rotate(2.3) + axes2 = ThreeDAxes().scale(2).rotate(2.3).shift([0,0,1.3]) + + #----f(x,y): sqrt(x**2+y**2) + p = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -math.sqrt(u**2+v**2) + ]),v_min = -1,v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [RED_C,TEAL_D], + resolution = (20, 20)).scale(1) + + #----size increased of f(x,y): sqrt(x**2+y**2) + p2 = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -math.sqrt(u**2+v**2) + ]),v_min = -1,v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [RED_C,TEAL_D], + resolution = (20, 20)).scale(3).shift([0,0,0]) + + self.set_camera_orientation(phi = 75 * DEGREES,theta = 40*DEGREES) + + d = Dot([0,0,0],color = '#800000') #---- critical point + d2 = Dot([0,0,1.5],color = '#800000').scale(2) #---- size increased of critical point + + f_text = TextMobject("$f$ is not differentiable at origin,because the surface").scale(0.5).to_corner(UL) + f2_text = TextMobject("is not flat when zoomed in at the origin.").scale(0.5).to_corner(UL).shift(0.5*DOWN) + + self.add(axes) + self.wait(1) + self.play(Write(p),Write(d)) + self.wait(1) + self.move_camera(phi = 50 * DEGREES,theta = 40*DEGREES) + self.wait(1) + self.play(ReplacementTransform(axes,axes2),ReplacementTransform(p,p2),ReplacementTransform(d,d2)) + self.wait(1) + self.add_fixed_in_frame_mobjects(f_text) + self.add_fixed_in_frame_mobjects(f2_text) + self.wait(2) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file4_Tangent_plane_at_extrema_and_saddle_point.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file4_Tangent_plane_at_extrema_and_saddle_point.gif Binary files differnew file mode 100644 index 0000000..3fe7992 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file4_Tangent_plane_at_extrema_and_saddle_point.gif diff --git a/FSF-2020/approximations-and-optimizations/Critical Points/types_of_cp.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file4_Tangent_plane_at_extrema_and_saddle_point.py index f9055e6..d129213 100644 --- a/FSF-2020/approximations-and-optimizations/Critical Points/types_of_cp.py +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Tangent-Plane-Approximations/file4_Tangent_plane_at_extrema_and_saddle_point.py @@ -1,12 +1,9 @@ -from manimlib.imports import * +from manimlib.imports import* -class TypescpAnimation(ThreeDScene): +class TangenttoSurface(ThreeDScene): def construct(self): - axes = ThreeDAxes() + axes = ThreeDAxes() - r_text = TextMobject("Relative Maximum at ORIGIN",color ='#87CEFA') - f_text = TextMobject("$f(x,y) = -x^2-y^2$").to_corner(UL) - #----graph of first function f(x,y) = -x**2-y**2 f = ParametricSurface( lambda u, v: np.array([ @@ -15,9 +12,7 @@ class TypescpAnimation(ThreeDScene): -u**2-v**2 ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [YELLOW_D, YELLOW_E], resolution = (20, 20)).scale(1) - - r2_text = TextMobject("Saddle Point at ORIGIN",color ='#87CEFA') - f2_text = TextMobject("$f(x,y) = -x^2+y^2$").to_corner(UL) + f_text = TextMobject("Tangent plane at relative maxima").to_corner(UL).scale(0.5) #----graph of second function f(x,y) = -x**2+y**2 f2 = ParametricSurface( @@ -27,9 +22,7 @@ class TypescpAnimation(ThreeDScene): -u**2+v**2 ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [RED_D, RED_E], resolution = (20, 20)).scale(1) - - r3_text = TextMobject("Relative Minimum at ORIGIN",color ='#87CEFA') - f3_text = TextMobject("$f(x,y) = x^2+y^2$").to_corner(UL) + f2_text = TextMobject("Tangent plane at saddle point").to_corner(UL).scale(0.5) #----graph of third function f(x,y) = x**2+y**2 f3 = ParametricSurface( @@ -39,32 +32,31 @@ class TypescpAnimation(ThreeDScene): u**2+v**2 ]),v_min = -1, v_max = 1, u_min = -1, u_max = 1, checkerboard_colors = [GREEN_D, GREEN_E], resolution = (20, 20)).scale(1) + f3_text = TextMobject("Tangent plane at relative minima").to_corner(UL).scale(0.5) self.set_camera_orientation(phi = 75 * DEGREES, theta = -45 * DEGREES ) - d = Dot(np.array([0,0,0]), color = '#800000') #---- critical point + d = Dot(np.array([0,0,0]), color = '#800000') #---- critical point - self.add_fixed_in_frame_mobjects(r_text) - self.wait(1) - self.play(FadeOut(r_text)) + r = Rectangle(height = 2,breadth = 1,color = PURPLE).scale(0.5) + + self.begin_ambient_camera_rotation(rate = 0.3) self.add(axes) self.play(Write(f),Write(d)) + self.wait(1) self.add_fixed_in_frame_mobjects(f_text) - self.wait(2) - self.play(FadeOut(axes),FadeOut(f),FadeOut(f_text),FadeOut(d)) - - self.add_fixed_in_frame_mobjects(r2_text) + self.play(ShowCreation(r)) + self.wait(1) + self.play(FadeOut(r),FadeOut(f),FadeOut(d),FadeOut(f_text)) self.wait(1) - self.play(FadeOut(r2_text)) - self.add(axes) self.play(Write(f2),Write(d)) + self.wait(1) self.add_fixed_in_frame_mobjects(f2_text) - self.wait(2) - self.play(FadeOut(axes),FadeOut(f2),FadeOut(f2_text),FadeOut(d)) - - self.add_fixed_in_frame_mobjects(r3_text) + self.play(ShowCreation(r)) + self.wait(1) + self.play(FadeOut(r),FadeOut(f2),FadeOut(d),FadeOut(f2_text)) self.wait(1) - self.play(FadeOut(r3_text)) - self.add(axes) self.play(Write(f3),Write(d)) + self.wait(1) self.add_fixed_in_frame_mobjects(f3_text) - self.wait(2) + self.play(ShowCreation(r)) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/README.md b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/README.md new file mode 100644 index 0000000..96b32bf --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/README.md @@ -0,0 +1,27 @@ +<h1><div align=”center”><b>SubTopic: The Second Derivative Test</b></h1></div> +<br/></br> + +<tab>file1_Second_order_partial_derivatives + + +<br/></br> +<br/></br> + +<tab>file2_Nondegenerate_Hessian_Matrix + + +<br/></br> +<br/></br> + +<tab>file3_Degenerate_Hessian_Matrix + + +<br/></br> +<br/></br> + +<tab>file4_Contour_Diagram + + +<br/></br> +<br/></br> + diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file1_Second_order_partial_derivatives.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file1_Second_order_partial_derivatives.gif Binary files differnew file mode 100644 index 0000000..3471e4d --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file1_Second_order_partial_derivatives.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file1_Second_order_partial_derivatives.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file1_Second_order_partial_derivatives.py new file mode 100644 index 0000000..84052cc --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file1_Second_order_partial_derivatives.py @@ -0,0 +1,78 @@ +from manimlib.imports import* + +#---- graphs of second-order partial derivatives of a function +class SurfacesAnimation(ThreeDScene): + def construct(self): + + axes = ThreeDAxes() + x_label = TextMobject('$x$').shift([5,0.5,0]) #---- x axis + y_label = TextMobject('$y$').shift([0.5,4,0]).rotate(-4.5) #---- y axis + + #---- surface of function: f(x,y) = (x^2+y^2)^2 + surface_f = ParametricSurface( + lambda u, v: np.array([ + u, + v, + ((u**2)+(v**2))**2 + ]),v_min=-1,v_max=1,u_min=-1,u_max=1,checkerboard_colors=[GREEN_D, GREEN_E]).scale(1) + + #---- surface of second-order partial derivative f_xx + surface_fxx = ParametricSurface( + lambda u, v: np.array([ + u, + v, + (3*u**2)+(v**2) + ]),v_min=-1,v_max=1,u_min=-1,u_max=1,checkerboard_colors=[YELLOW_D, YELLOW_E]).shift([0,0,0]).scale(0.6) + + #---- surface of second-order partial derivative f_yy + surface_fyy = ParametricSurface( + lambda u, v: np.array([ + u, + v, + (u**2)+(3*v**2) + ]),v_min=-1,v_max=1,u_min=-1,u_max=1,checkerboard_colors=[PURPLE_D, PURPLE_E]).scale(0.6).shift([0,0,0]) + + #---- surface of second-order partial derivative f_xy = f_yx + surface_fxy = ParametricSurface( + lambda u, v: np.array([ + u, + v, + 8*u*v + ]),v_min=-1,v_max=1,u_min=-1,u_max=1,checkerboard_colors=[TEAL_D, TEAL_E]).scale(0.6) + + f_text= TextMobject("$f(x,y) = (x^2+y^2)^2$",color = GREEN).scale(0.7).to_corner(UL) + + fxx_text= TextMobject("$f_{xx} = 12x^2+4y^2$ (Concavity along x axis)",color = YELLOW).scale(0.5).to_corner(UL) + + fyy_text= TextMobject("$f_{yy} = 4x^2+12y^2$(Concavity along y axis)",color = PURPLE).scale(0.5).to_corner(UL) + + fxy_text= TextMobject("$f_{xy} = f_{yx} = 8xy$ (Twisting of the function)",color = TEAL).scale(0.5).to_corner(UL) + + + self.set_camera_orientation(phi = 40 * DEGREES, theta = 45 * DEGREES) + self.begin_ambient_camera_rotation(rate = 0.1) + self.add_fixed_in_frame_mobjects(f_text) + self.add(axes) + self.add(x_label) + self.add(y_label) + self.wait(1) + self.play(Write(surface_f)) + self.wait(2) + self.play(FadeOut(f_text)) + + + self.play(ReplacementTransform(surface_f,surface_fxx)) + + self.add_fixed_in_frame_mobjects(fxx_text) + self.wait(2) + self.play(FadeOut(fxx_text)) + + self.play(ReplacementTransform(surface_fxx,surface_fyy)) + self.add_fixed_in_frame_mobjects(fyy_text) + self.wait(2) + self.play(FadeOut(fyy_text)) + + self.play(ReplacementTransform(surface_fyy,surface_fxy)) + self.move_camera(phi = 35 * DEGREES, theta = 80 * DEGREES) + self.add_fixed_in_frame_mobjects(fxy_text) + self.wait(2) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file2_Nondegenerate_Hessian_Matrix.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file2_Nondegenerate_Hessian_Matrix.gif Binary files differnew file mode 100644 index 0000000..0d58b4f --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file2_Nondegenerate_Hessian_Matrix.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file2_Nondegenerate_Hessian_Matrix.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file2_Nondegenerate_Hessian_Matrix.py new file mode 100644 index 0000000..32c1559 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file2_Nondegenerate_Hessian_Matrix.py @@ -0,0 +1,158 @@ +from manimlib.imports import* +import math as m + +class Minima(ThreeDScene): + def construct(self): + + heading = TextMobject("Nondegenerate Hessian Matrix",color = BLUE) + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.3,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.3,5.5,0]).rotate(-4.5) #---- y axis + + h_text = TextMobject("Case 1: $\\frac{\\partial^2 f}{\\partial x^2}>0$ and $\\frac{\\partial^2 f}{\\partial y^2}>0$").scale(1) + + #---- determiniant of Hessian Matrix + hessian_surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -0.5*m.exp(-u**2-v**2) + ]),u_min = -PI, u_max = PI, v_min = -PI, v_max =PI).set_color(TEAL).shift([0,0,0]).scale(1).fade(0.2) + + det_text= TextMobject("$det \\hspace{1mm} H = (\\frac{\\partial^2 f}{\\partial x^2})(\\frac{\\partial^2 f}{\\partial y^2})-(\\frac{\\partial^2 f}{\\partial x \\partial y})^2 $").to_corner(UL).scale(0.7) + + #---- function f(x,y) + f_surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + u**2+v**2 + ]),u_min = -1.3, u_max = 1.3, v_min = -1.3, v_max = 1.3).set_color(TEAL).shift([0,0,-0.5]) + + f_text= TextMobject("surface of the function").to_corner(UL).scale(0.8) + + d = Dot(color = "#800000").shift([0,0,-0.52]) #---- critical point + + self.set_camera_orientation(phi = 75*DEGREES, theta = 40*DEGREES) + self.add_fixed_in_frame_mobjects(heading) + self.wait(1) + self.play(FadeOut(heading)) + self.wait(1) + self.add_fixed_in_frame_mobjects(h_text) + self.wait(1) + self.play(FadeOut(h_text)) + self.wait(1) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.play(Write(hessian_surface)) + self.wait(1) + self.add_fixed_in_frame_mobjects(det_text) + self.move_camera(phi = 90*DEGREES, theta= 60*DEGREES) + self.play(Write(d)) + self.wait(1) + self.play(FadeOut(det_text),ReplacementTransform(hessian_surface,f_surface)) + self.wait(1) + self.add_fixed_in_frame_mobjects(f_text) + self.wait(1) + self.play(FadeOut(f_text),FadeOut(f_surface),FadeOut(axes),FadeOut(label_x),FadeOut(label_y),FadeOut(d)) + +class Maxima(ThreeDScene): + def construct(self): + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.3,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.3,5.5,0]).rotate(-4.5) #---- y axis + + h_text = TextMobject("Case 2: $\\frac{\\partial^2 f}{\\partial x^2}<0$ and $\\frac{\\partial^2 f}{\\partial y^2}<0$").scale(1) + + #---- determiniant of Hessian Matrix + hessian_surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + 0.5*m.exp(-u**2-v**2) + ]),u_min = -PI, u_max = PI, v_min = -PI, v_max =PI).set_color(TEAL).shift([0,0,0]).scale(1).fade(0.2) + + det_text= TextMobject("$det \\hspace{1mm} H = (\\frac{\\partial^2 f}{\\partial x^2})(\\frac{\\partial^2 f}{\\partial y^2})-(\\frac{\\partial^2 f}{\\partial x \\partial y})^2 $").to_corner(UL).scale(0.7) + + #---- function g(x,y) + g_surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -u**2-v**2 + ]),u_min = -1.3, u_max = 1.3, v_min = -1.3, v_max = 1.3).set_color(TEAL).shift([0,0,0.5]) + + g_text= TextMobject("surface of the function").to_corner(UL).scale(0.8) + + d = Dot(color = "#800000").shift([0,0,0.5]) #---- critical point + + self.set_camera_orientation(phi = 75*DEGREES, theta = 40*DEGREES) + self.add_fixed_in_frame_mobjects(h_text) + self.wait(1) + self.play(FadeOut(h_text)) + self.wait(1) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.play(Write(hessian_surface)) + self.wait(1) + self.add_fixed_in_frame_mobjects(det_text) + self.play(Write(d)) + self.wait(1) + self.play(FadeOut(det_text),ReplacementTransform(hessian_surface,g_surface)) + self.wait(1) + self.add_fixed_in_frame_mobjects(g_text) + self.wait(1) + self.play(FadeOut(g_text),FadeOut(g_surface),FadeOut(axes),FadeOut(label_x),FadeOut(label_y),FadeOut(d)) + +class SaddlePoint(ThreeDScene): + def construct(self): + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.3,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.3,5.5,0]).rotate(-4.5) #---- y axis + + h_text = TextMobject("Case 3: $\\frac{\\partial^2 f}{\\partial x^2}$ and $\\frac{\\partial^2 f}{\\partial y^2}$ have opposite signs").scale(1) + + #---- determiniant of Hessian Matrix + hessian_surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + m.exp(0.5*u**2-0.5*v**2) + ]),u_min = -1.2, u_max = 1.2, v_min = -2.5, v_max = 2.5).set_color(TEAL).shift([0,0,-1]).scale(1).fade(0.2) + + det_text= TextMobject("$det \\hspace{1mm} H = (\\frac{\\partial^2 f}{\\partial x^2})(\\frac{\\partial^2 f}{\\partial y^2})-(\\frac{\\partial^2 f}{\\partial x \\partial y})^2 $").to_corner(UL).scale(0.7) + + #---- function p(x,y) + p_surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + u**2-v**2 + ]),u_min = -1, u_max = 1, v_min = -1, v_max =1).set_color(TEAL).shift([0,0,0]).scale(2) + + p_text= TextMobject("surface of the function").to_corner(UL).scale(0.8) + + d = Dot(color = "#800000").shift([0,0,0]) #---- critical point + + self.set_camera_orientation(phi = 80*DEGREES, theta = 60*DEGREES) + self.add_fixed_in_frame_mobjects(h_text) + self.wait(1) + self.play(FadeOut(h_text)) + self.wait(1) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.wait(1) + self.play(Write(hessian_surface)) + self.play(Write(d)) + self.wait(1) + self.add_fixed_in_frame_mobjects(det_text) + self.wait(2) + self.play(FadeOut(det_text),ReplacementTransform(hessian_surface,p_surface)) + self.add_fixed_in_frame_mobjects(p_text) + self.wait(2) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file3_Degenerate_Hessian_Matrix.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file3_Degenerate_Hessian_Matrix.gif Binary files differnew file mode 100644 index 0000000..5aae300 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file3_Degenerate_Hessian_Matrix.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file3_Degenerate_Hessian_Matrix.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file3_Degenerate_Hessian_Matrix.py new file mode 100644 index 0000000..9310553 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file3_Degenerate_Hessian_Matrix.py @@ -0,0 +1,45 @@ +from manimlib.imports import* +import math as m + +class DegenerateHessian(ThreeDScene): + def construct(self): + + heading = TextMobject("Degenerate Hessian Matrix",color = BLUE) + + h_text = TextMobject("For $det \\hspace{1mm} H = 0$, the surface of the function at the critical point would be flat.").scale(0.7) + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.3,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.3,5.5,0]).rotate(-4.5) #---- y axis + + #---- function f(x,y) + f_surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + -u**4-v**4 + ]),u_min = -0.8, u_max = 0.8, v_min = -0.8, v_max = 0.8).set_color(TEAL).shift([0,0,-0.5]).scale(2) + + f_text= TextMobject("surface of the function").to_corner(UL).scale(0.5) + + d = Dot(color = "#800000").shift([0,0,-0.5]) #---- critical point + plane = Square(color = YELLOW,fill_opacity= 0.2).shift([0,0,-0.5]).scale(1.3) + + self.set_camera_orientation(phi = 70*DEGREES, theta = 45*DEGREES) + self.add_fixed_in_frame_mobjects(heading) + self.wait(1) + self.play(FadeOut(heading)) + self.add_fixed_in_frame_mobjects(h_text) + self.wait(2) + self.play(FadeOut(h_text)) + self.wait(1) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.play(Write(f_surface)) + self.add_fixed_in_frame_mobjects(f_text) + self.wait(1) + self.play(Write(d)) + self.wait(1) + self.play(Write(plane)) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file4_Contour_Diagram.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file4_Contour_Diagram.gif Binary files differnew file mode 100644 index 0000000..41068e2 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file4_Contour_Diagram.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file4_Contour_Diagram.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file4_Contour_Diagram.py new file mode 100644 index 0000000..d3084e2 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/The-Second-Derivative-Test/file4_Contour_Diagram.py @@ -0,0 +1,120 @@ +from manimlib.imports import* + +#---- contour diagram animation +class ContourDiagram(ThreeDScene): + def construct(self): + + heading = TextMobject("CONTOUR DIAGRAM", color = YELLOW).scale(1) + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.5,0]) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5) #---- y axis + + #---- surface of a paraboloid + surface = ParametricSurface( + lambda u, v: np.array([ + np.cos(v)*u, + np.sin(v)*u, + u**2 + ]),v_min = -2, v_max = 2, u_min = -2, u_max = 2, checkerboard_colors = [GREEN_B,GREEN_C,GREEN_D,GREEN_E]).shift([0,0,0]).scale(0.5) + + #---- first contour projection + contour1 = ParametricSurface( + lambda u, v: np.array([ + np.cos(TAU * v), + np.sin(TAU * v), + 2*(1 - 2.5*u) + ])).fade(0.5).scale(0.21).shift([0,0,1.01]) + + #---- first contour line + c_1 = Circle(color = BLUE).scale(0.21).shift([0,0,0]).rotate(0.1,DOWN) + + #------------------------------------------------- + + #---- second contour projection + contour2 = ParametricSurface( + lambda u, v: np.array([ + np.cos(TAU * v), + np.sin(TAU * v), + 2*(1 - 1.6*u) + ])).fade(0.5).scale(0.41).shift([0,0,0.3]).set_color(RED) + + #---- second contour line + c_2 = Circle(color = RED).scale(0.41).shift([0,0,0]).rotate(0.1,DOWN) + + #------------------------------------------------- + + #---- third contour projection + contour3 = ParametricSurface( + lambda u, v: np.array([ + np.cos(TAU * v), + np.sin(TAU * v), + 2*(1 - 1.5*u) + ])).fade(0.5).scale(0.61).shift([0,0,0.4]).set_color(YELLOW) + + #---- third contour line + c_3 = Circle(color = YELLOW).scale(0.61).shift([0,0,0]) + + #------------------------------------------------- + + #---- fourth contour projection + contour4 = ParametricSurface( + lambda u, v: np.array([ + np.cos(TAU * v), + np.sin(TAU * v), + 2*(1 - 1.5*u) + ])).fade(0.7).scale(0.81).shift([0,0,0.7]).set_color(PINK) + + #---- fourth contour line + c_4 = Circle(color = PINK).scale(0.81).shift([0,0,0]) + + #------------------------------------------------- + + #---- fifth contour projection + contour5 = ParametricSurface( + lambda u, v: np.array([ + np.cos(TAU * v), + np.sin(TAU * v), + 2*(1 - 1.5*u) + ])).fade(0.7).scale(1.01).shift([0,0,1]).set_color(PURPLE) + + #---- fifth contour line + c_5 = Circle(color = PURPLE).scale(1.01).shift([0,0,0]) + + c_text= TextMobject("Contour Lines").scale(0.5).shift(2*DOWN) + s = Square().scale(1.3) + + self.set_camera_orientation(phi = 75 * DEGREES, theta = 10 * DEGREES) + self.add_fixed_in_frame_mobjects(heading) + self.wait(1) + self.play(FadeOut(heading)) + self.wait(1) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.play(Write(surface)) + self.wait(1) + self.add(contour1) + self.wait(1) + self.play(Write(c_1)) + self.play(ReplacementTransform(contour1,contour2)) + self.wait(1) + self.play(Write(c_2)) + self.play(ReplacementTransform(contour2,contour3)) + self.wait(1) + self.play(Write(c_3)) + self.play(ReplacementTransform(contour3,contour4)) + self.wait(1) + self.play(Write(c_4)) + self.play(ReplacementTransform(contour4,contour5)) + self.wait(1) + self.play(Write(c_5)) + self.wait(1) + self.play(FadeOut(contour5),FadeOut(axes),FadeOut(label_x),FadeOut(label_y),FadeOut(surface),FadeOut(contour5),FadeOut(contour4),FadeOut(contour3),FadeOut(contour2),FadeOut(contour1)) + self.wait(1) + self.move_camera(phi=0 * DEGREES,theta= 90*DEGREES) + self.wait(1) + self.add_fixed_in_frame_mobjects(c_text) + self.wait(1) + self.play(ShowCreation(s),FadeOut(c_text)) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/README.md b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/README.md new file mode 100644 index 0000000..ce4da11 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/README.md @@ -0,0 +1,34 @@ +<h1><div align=”center”><b>SubTopic: Total Differential</b></h1></div> +<br/></br> + +<tab>file1_Visualization_of_dz + + +<br/></br> +<br/></br> + +<tab>file2_Differentials + + + +<br/></br> +<br/></br> + +<tab>file3_Total_differential_of_z + + +<br/></br> +<br/></br> + +<tab>file4_total_differential_change + + +<br/></br> +<br/></br> + +<tab>file5_Total_differential_approximation + +  + +<br/></br> +<br/></br> diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file1_Visualization_of_dz.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file1_Visualization_of_dz.gif Binary files differnew file mode 100644 index 0000000..2e148af --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file1_Visualization_of_dz.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file1_Visualization_of_dz.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file1_Visualization_of_dz.py new file mode 100644 index 0000000..1fdd0b9 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file1_Visualization_of_dz.py @@ -0,0 +1,59 @@ +from manimlib.imports import* + +#---- visualization of total differential dz between two points lying on the surface of the function +class differentialdz(ThreeDScene): + + def construct(self): + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.5,0]).fade(0.4) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5).fade(0.4) #---- y axis + + #---- surface of the funtion f(x,y) + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + u**2+v**2 + ]),u_min=-1,u_max=1, v_min=-1,v_max=1).set_color("#FF69B4").fade(0.6).scale(2).shift(3*UP+1*LEFT) + + d = Dot([1.4,1.75,1],color = '#00FFFF').rotate(1.571,UP) #---- point on the surface + d2 = Dot([2,2,1],color = '#00FFFF').rotate(1.571,UP) #---- point on the surface + + p1 = TextMobject("$P_1$",color ='#ADFF2F').scale(0.6).shift(2*RIGHT+1*UP) + p2 = TextMobject("$P_2$",color = '#ADFF2F').scale(0.6).shift(2.6*RIGHT+0.9*UP) + + l = DashedLine(color = '#800000').rotate(1.571,UP).scale(1).shift(1.7*UP+1.6*RIGHT) + l2 = DashedLine(color = '#800000').rotate(1.571,UP).scale(0.8).shift(2.26*UP+1.2*RIGHT) + + l_text = TextMobject("$(x_1,y_1)$",color = '#ADFF2F').scale(0.6).shift(2*RIGHT+1.6*DOWN) + l2_text = TextMobject("$(x_2,y_2)$",color = '#ADFF2F').scale(0.6).shift(2.7*RIGHT+1.2*DOWN) + + a = Arrow(color = '#FFFACD').scale(0.7).rotate(1.38,RIGHT).shift(2.5*LEFT+3.1*UP) + + a_text = TextMobject("$dz$",color='#800000').scale(0.5).shift(2.3*RIGHT+0.5*UP) + + plane = Rectangle(color = '#E6E6FA',fill_opacity = 1).scale(3).shift(1*RIGHT+3*UP).fade(0.9) + + label = TextMobject("$z = f(x,y)$").scale(0.6).shift(3.5*RIGHT+1.8*UP) + + self.set_camera_orientation(phi=75*DEGREES,theta=-10*DEGREES) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.wait(1) + self.play(Write(plane)) + self.play(Write(surface)) + self.add_fixed_in_frame_mobjects(label) + self.wait(1) + self.play(ShowCreation(l),ShowCreation(l2),Write(d),Write(d2)) + self.wait(1) + self.add_fixed_in_frame_mobjects(p1) + self.add_fixed_in_frame_mobjects(p2) + self.wait(1) + self.add_fixed_in_frame_mobjects(l_text) + self.add_fixed_in_frame_mobjects(l2_text) + self.play(ShowCreation(a)) + self.wait(1) + self.add_fixed_in_frame_mobjects(a_text) + self.wait(2) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file2_Differentials.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file2_Differentials.gif Binary files differnew file mode 100644 index 0000000..6baf271 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file2_Differentials.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file2_Differentials.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file2_Differentials.py new file mode 100644 index 0000000..1025210 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file2_Differentials.py @@ -0,0 +1,77 @@ +from manimlib.imports import* + +#---- visualization of the differentials along the axes +class differentials(ThreeDScene): + def construct(self): + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.3,0]).fade(0.4) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5).fade(0.4) #---- y axis + + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + u**2+v**2 + ]),u_min=-1,u_max=1, v_min=-1,v_max=1).set_color("#FF69B4").shift([0,2.5,0.3]).scale(1.2) #----surface z = f(x,y) + + + + plane = Rectangle(color = '#E6E6FA',fill_opacity = 1).scale(3).shift(-1*RIGHT+3*UP).fade(0.9) + + d = Dot([1,2,1],color = '#9400D3').rotate(1.571,UP) + d2 = Dot([2,2.9,1],color = '#9400D3').rotate(1.571,UP) + + p1 = TextMobject("$P_1$",color ='#ADFF2F').scale(0.6).shift(2*RIGHT+1*UP) + p2 = TextMobject("$P_2$",color = '#ADFF2F').scale(0.6).shift(2.6*RIGHT+0.4*UP) + + + l1 = DashedLine(color = '#00BFFF').scale(1.6).shift(3.5*UP+3.25*LEFT).rotate(1.571) + l2 = DashedLine(color = '#00BFFF').scale(1).shift(4*UP+2*LEFT).rotate(1.571) + + label_dz= TextMobject("$dz$").scale(0.4).shift(5.3*RIGHT+0.4*UP) + + + l3 = Line(color = '#FFDAB9').scale(0.8).shift(1.95*UP+0.7*RIGHT).rotate(1.571,DOWN).fade(0.2) + l4 = Line(color = '#FFDAB9').scale(0.6).shift(2.86*UP+0.9*RIGHT).rotate(1.571,DOWN).fade(0.2) + + line_y1 = DashedLine(color = '#00BFFF').scale(1.3).shift(0.82*UP+3.25*RIGHT).rotate(1.571) + line_y2 = DashedLine(color = '#00BFFF').scale(1.7).shift(1.2*UP+2.8*RIGHT).rotate(1.571) + + label_dy= TextMobject("$dy$").scale(0.6).shift(3*RIGHT+0.8*DOWN).rotate(math.radians(90)) + + line_x1 = DashedLine(color = '#00BFFF').scale(1.5).shift(2.2*UP+1.6*RIGHT).rotate(1.571,RIGHT) + line_x2 = DashedLine(color = '#00BFFF').scale(1.2).shift(2.9*UP+1.6*RIGHT).rotate(1.571,RIGHT) + + label_dx= TextMobject("$dx$").scale(0.4).shift(-0.4*UP+2.5*RIGHT) + + label = TextMobject("$f(x,y)$").scale(0.6).shift(4*RIGHT+3*UP) + + + self.set_camera_orientation(phi=75*DEGREES,theta=10*DEGREES) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.play(Write(plane)) + self.play(Write(surface)) + self.add_fixed_in_frame_mobjects(label) + self.wait(1) + self.play(Write(d),Write(d2)) + self.add_fixed_in_frame_mobjects(p1) + self.add_fixed_in_frame_mobjects(p2) + self.wait(1) + self.play(Write(l1)) + self.play(Write(l2)) + self.add_fixed_in_frame_mobjects(label_dz) + self.wait(1) + self.play(Write(l3)) + self.play(Write(l4)) + self.wait(1) + self.play(Write(line_y1)) + self.play(Write(line_y2)) + self.play(ShowCreation(label_dy)) + self.wait(1) + self.play(Write(line_x1)) + self.play(Write(line_x2)) + self.add_fixed_in_frame_mobjects(label_dx) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file3_Total_differential_of_z.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file3_Total_differential_of_z.gif Binary files differnew file mode 100644 index 0000000..a54d2da --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file3_Total_differential_of_z.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file3_Total_differential_of_z.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file3_Total_differential_of_z.py new file mode 100644 index 0000000..b8d6f96 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file3_Total_differential_of_z.py @@ -0,0 +1,100 @@ +from manimlib.imports import* + +#---- visualization of total differential definition +class totaldifferential(ThreeDScene): + def construct(self): + axes = ThreeDAxes().fade(0.5) + surface = ParametricSurface( + lambda u, v: np.array([ + u, + v, + u**2+v**2 + ]),u_min=-1,u_max=1, v_min=-1,v_max=1).set_color("#FF69B4").fade(0.6).shift([1,0.8,1.5]).scale(2) + + plane = Rectangle(color = '#E6E6FA',fill_opacity = 1).scale(3).shift(-1*RIGHT+3*UP).fade(0.9) + label_x = TextMobject("$x$").shift(5*RIGHT+0.4*DOWN).rotate(1.571) + label_y = TextMobject("$y$").shift(0.3*DOWN+5.6*RIGHT).scale(0.5) + label_z = TextMobject("$z$").shift(3.5*UP+0.2*LEFT).scale(0.5) + + s1 = Square(color = '#00FF00',fill_opacity=0.4).shift([1,1,0]) + s2 = Square(color = '#00FF00',fill_opacity=0.4).shift([1,1,3]).scale(0.95) + + l1 = Line([2,0,3],[2,0,0],color = '#FFFACD') + l2 = Line([0,2,3],[0,2,0],color = '#FFFACD') + l3 = Line([2,1.95,3],[2,2,0],color = '#FFFACD') + + d1 = Dot([2,0,1.5],color = '#FFD700').rotate(1.571,UP) + d1_text = TextMobject("$P1$").scale(0.4).shift(1.2*LEFT+1.1*UP) + + d2 = Dot([0,2,3],color = '#FFD700').rotate(1.571,UP) + d2_text = TextMobject("$P2$").scale(0.4).shift(2.3*RIGHT+3.1*UP) + + d3 = Dot([2,2,2],color = '#FFD700').rotate(1.571,UP) + d3_text = TextMobject("$Q$").scale(0.4).shift([1.6,-1,0]+2.5*UP) + + s3 = Square().shift([1,1,1.5]).scale(0.95) + s4 = Square().shift([1,1,2]).scale(0.95) + + m1_line = DashedLine([2,0,1.5],[2,2,2],color = '#87CEEB') + m2_line = DashedLine([2,2,2],[0,2,3],color = '#87CEEB') + + dx_line = Line([2,2,0],[4,2,0],color = '#00FF7F') + dy_line = Line([2,2,0],[2,4,0],color = '#00FF7F') + + dx = DashedLine([3.5,0,0],[3.5,2,0],color = '#87CEEB') + dy = DashedLine([0,3.5,0],[2,3.5,0],color = '#87CEEB') + + dx_text = TextMobject("$dx$").scale(0.8).shift([4,1,0]).rotate(1.571) + dy_text = TextMobject("$dy$").scale(0.8).shift([1,3.8,0]).rotate(math.radians(180)) + + parx_line = Line([0,2,1.5],[0,5,1.5],color = '#00FF7F') + parm_line = Line([0,2,2],[0,5,2],color = '#00FF7F') + pary_line = Line([0,2.1,3],[0,5,3],color = '#00FF7F') + + delx = DashedLine([0,4,2],[0,4,1.5],color = '#F0F8FF') + dely = DashedLine([0,4,3],[0,4,2],color = '#FAEBD7') + + dely_text = TextMobject("$\\frac{\\partial z}{\\partial y}dy$").shift(4.6*RIGHT+2.3*UP).scale(0.4) + delx_text = TextMobject("$\\frac{\\partial z}{\\partial x}dx$").shift(4.6*RIGHT+1.4*UP).scale(0.4) + + + self.set_camera_orientation(phi=75*DEGREES,theta=20*DEGREES) + self.add(axes) + self.play(Write(plane)) + self.play(ShowCreation(label_x)) + self.add_fixed_in_frame_mobjects(label_y) + self.add_fixed_in_frame_mobjects(label_z) + self.wait(1) + self.play(Write(surface)) + self.play(ShowCreation(d1)) + self.add_fixed_in_frame_mobjects(d1_text) + self.play(ShowCreation(d2)) + self.add_fixed_in_frame_mobjects(d2_text) + self.wait(1) + self.play(Write(s2)) + self.wait(1) + self.play(Write(l1),Write(l2),Write(l3)) + self.wait(1) + self.play(Write(s1)) + self.wait(1) + self.play(FadeOut(surface)) + self.play(ShowCreation(d3)) + self.add_fixed_in_frame_mobjects(d3_text) + self.play(ShowCreation(m1_line)) + self.play(ShowCreation(m2_line)) + self.wait(1) + self.play(ShowCreation(dx_line),ShowCreation(dx),ShowCreation(dx_text)) + self.wait(1) + self.play(ShowCreation(dy_line),ShowCreation(dy),ShowCreation(dy_text)) + self.wait(2) + self.play(Write(s3)) + self.play(Write(s4)) + self.wait(1) + self.play(ShowCreation(parx_line),ShowCreation(parm_line),ShowCreation(pary_line)) + self.wait(1) + self.play(ShowCreation(dely)) + self.add_fixed_in_frame_mobjects(dely_text) + self.wait(1) + self.play(ShowCreation(delx)) + self.add_fixed_in_frame_mobjects(delx_text) + self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file4_total_differential_change.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file4_total_differential_change.gif Binary files differnew file mode 100644 index 0000000..f2227a8 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file4_total_differential_change.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file4_total_differential_change.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file4_total_differential_change.py new file mode 100644 index 0000000..78e41a2 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file4_total_differential_change.py @@ -0,0 +1,54 @@ +from manimlib.imports import* + + +class firstScene(ThreeDScene): + + def construct(self): + + axes = ThreeDAxes() + + s = Rectangle(color = '#F08080',fill_opacity=1).fade(0.7).shift(1.9*UP+5*LEFT).scale(0.9)#----surface z = f(x,y) + + s2= Rectangle(color = '#F08080',fill_opacity=1).fade(0.7).shift(2.4*UP+3.1*RIGHT).scale(0.6) #----reflection of the surface on the x-y plane + + l1 = DashedLine(color = '#AFEEEE').rotate(1.571,UP).scale(1).shift(1.53*UP+1.5*RIGHT) + l2 = DashedLine(color = '#AFEEEE').rotate(1.571,UP).scale(1).shift(2.9*UP+1.4*RIGHT) + l3 = DashedLine(color = '#AFEEEE').rotate(1.571,UP).scale(1).shift(1.5*UP-1.6*RIGHT) + l4 = DashedLine(color = '#AFEEEE').rotate(1.571,UP).scale(1).shift(2.9*UP-1.75*RIGHT) + + + l1_text = TextMobject("$(x+\\triangle x,y)$").shift(RIGHT+1.7*DOWN).scale(0.4) + l2_text = TextMobject("$(x+\\triangle x,y+\\triangle y)$").shift(3*RIGHT+1.8*DOWN).scale(0.4) + l3_text = TextMobject("$f(x,y)$").shift(1.6*RIGHT+1.5*UP).scale(0.4) + l4_text = TextMobject("$(x,y+\\triangle y)$").shift(3.5*RIGHT+0.7*DOWN).scale(0.4) + + label_x = TextMobject("$x$").shift(5*RIGHT+0.4*DOWN) + label_y = TextMobject("$y$").shift(5*UP-0.6*RIGHT) + + self.add(axes) + self.set_camera_orientation(phi=75*DEGREES,theta=10*DEGREES) + self.wait(1) + self.play(ShowCreation(label_x),ShowCreation(label_y)) + self.play(Write(s)) + self.wait(1) + self.add_fixed_in_frame_mobjects(l3_text) + self.wait(1) + self.play(Write(l3)) + self.wait(1) + self.play(Write(l1)) + self.add_fixed_in_frame_mobjects(l1_text) + self.wait(1) + self.play(Write(l2)) + self.add_fixed_in_frame_mobjects(l2_text) + self.wait(1) + self.play(Write(l4)) + self.add_fixed_in_frame_mobjects(l4_text) + self.wait(1) + self.play(Write(s2)) + self.wait(1) + + + + + + diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file5_Total_differential_approximation.gif b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file5_Total_differential_approximation.gif Binary files differnew file mode 100644 index 0000000..ebbf240 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file5_Total_differential_approximation.gif diff --git a/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file5_Total_differential_approximation.py b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file5_Total_differential_approximation.py new file mode 100644 index 0000000..e7b39bb --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/approximations-and-optimizations/Total-Differential/file5_Total_differential_approximation.py @@ -0,0 +1,52 @@ +from manimlib.imports import* + +#---- approximation value of function between two points using total differentials +class approximation(ThreeDScene): + + def construct(self): + + axes = ThreeDAxes() + label_x = TextMobject("$x$").shift([5.5,-0.3,0]).fade(0.4) #---- x axis + label_y = TextMobject("$y$").shift([-0.5,5.5,0]).rotate(-4.5).fade(0.4) #---- y axis + + surface = ParametricSurface( + lambda u, v: np.array([ + np.sin(u), + v, + -u**2-v + ]),u_min=-1,u_max=1, v_min=-1,v_max=1).set_color("#00008B").scale(2).shift(3.8*UP+2*LEFT) + + d = Dot([1.4,1.75,1],color = '#00FFFF').rotate(1.571,UP) + d2 = Dot([2,2,1],color = '#00FFFF').rotate(1.571,UP) + + l = DashedLine(color = '#800000').rotate(1.571,UP).scale(1).shift(1.7*UP+1.6*RIGHT) + l2 = DashedLine(color = '#800000').rotate(1.571,UP).scale(0.8).shift(2.26*UP+1.2*RIGHT) + + l_text = TextMobject("$(x_1,y_1)$",color = '#ADFF2F').scale(0.6).shift(2*RIGHT+1.6*DOWN) + l2_text = TextMobject("$(x_2,y_2)$",color = '#ADFF2F').scale(0.6).shift(2.7*RIGHT+1.2*DOWN) + + plane = Rectangle(color = '#E6E6FA',fill_opacity = 1).scale(3).shift(1*RIGHT+3*UP).fade(0.9) + + tangentplane = Rectangle(color = '#E6E6FA',fill_opacity = 1).scale(1.1).shift(2*LEFT+3.4*UP).fade(0.5).rotate(0.8,RIGHT) + tangentplane_text = TextMobject("Tangent Plane").scale(0.4).shift(3*RIGHT+1*UP) + + label = TextMobject("$z = f(x,y)$").scale(0.6).shift(4*RIGHT+3*UP) + + self.set_camera_orientation(phi=75*DEGREES,theta=-10*DEGREES) + self.add(axes) + self.add(label_x) + self.add(label_y) + self.wait(1) + self.play(Write(plane)) + self.wait(1) + self.play(Write(surface)) + self.add_fixed_in_frame_mobjects(label) + self.wait(1.5) + self.play(ShowCreation(l),ShowCreation(l2),Write(d),Write(d2)) + self.wait(1) + self.add_fixed_in_frame_mobjects(l_text) + self.add_fixed_in_frame_mobjects(l2_text) + self.wait(1) + self.play(Write(tangentplane)) + self.add_fixed_in_frame_mobjects(tangentplane_text) + self.wait(2) diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/README.md b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/README.md new file mode 100644 index 0000000..10786d6 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/README.md @@ -0,0 +1,11 @@ +**file1_simple_visualization.py** <br> + + +**file2_circle_curvature.py** <br> + + +**file3_curvature_interpretation.py** <br> + + +**file4_different_curvature_single_curve.py** <br> + diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file1_simple_visualization.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file1_simple_visualization.gif Binary files differnew file mode 100644 index 0000000..3f7ecd1 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file1_simple_visualization.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file1_simple_visualization.py b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file1_simple_visualization.py index 7ab8908..45058d7 100644 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file1_simple_visualization.py +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file1_simple_visualization.py @@ -32,6 +32,8 @@ class randomcurve(GraphScene): dot6 = Dot(tgt6.get_start(), color = RED) dot7 = Dot(tgt7.get_start(), color = RED) + arc = ArcBetweenPoints(dot1.get_center(), dot2.get_center(), color = GREEN_SCREEN, angle = 10*DEGREES).rotate(180*DEGREES) + dots = VGroup(*[dot1, dot2, dot3, dot4, dot5, dot6, dot7]) ds = CurvedArrow((-4, 2, 0), (tgt1.get_start() + tgt2.get_start()) / 2, color = YELLOW) @@ -43,15 +45,13 @@ class randomcurve(GraphScene): self.wait(2) self.play(FadeOut(intro)) self.setup_axes(hideaxes=False) - self.play(ShowCreation(graphobj), FadeIn(dots), FadeIn(ds), FadeIn(ds_text)) + self.play(ShowCreation(graphobj), FadeIn(dots), FadeIn(ds), FadeIn(ds_text), FadeIn(arc)) self.wait(1) - self.play(FadeOut(self.axes), FadeOut(graphobj),FadeIn(mid), FadeOut(dots), FadeOut(ds), FadeOut(ds_text)) - self.wait(2) + self.play(FadeOut(self.axes), FadeOut(arc), FadeOut(graphobj),FadeIn(mid), FadeOut(dots), FadeOut(ds), FadeOut(ds_text)) + self.wait(3) self.play(FadeOut(mid)) self.play(FadeIn(self.axes), FadeIn(graphobj), FadeIn(dots)) - - tangents = [tgt1, tgt2, tgt3, tgt4, tgt5, tgt6, tgt7] for tangent in tangents: self.play(ShowCreation(tangent), run_time = 0.2) @@ -60,7 +60,7 @@ class randomcurve(GraphScene): self.play(FadeOut(self.axes), FadeOut(graphobj), FadeOut(tangents), FadeOut(dots)) self.wait(1) self.play(FadeIn(outro)) - self.wait(2) + self.wait(3) self.play(FadeOut(outro)) self.wait(1) diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file2_circle_curvature.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file2_circle_curvature.gif Binary files differnew file mode 100644 index 0000000..989a3b7 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file2_circle_curvature.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file3_curvature_interpretation.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file3_curvature_interpretation.gif Binary files differnew file mode 100644 index 0000000..22a450a --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file3_curvature_interpretation.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file3_curvature_interpretation.py b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file3_curvature_interpretation.py new file mode 100644 index 0000000..d8dd0a4 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file3_curvature_interpretation.py @@ -0,0 +1,42 @@ +from manimlib.imports import * + +class interpretation(Scene): + def construct(self): + tgt = Vector((1, 2, 0), color = YELLOW) + tgtText = TextMobject(r'$r\prime (t)$').next_to(tgt, UP, buff = 0).scale(0.7) + tgt2 = DashedLine((0,0,0),(1, 2, 0), color = GRAY).shift(DOWN + 2*RIGHT) + + nm = Vector((2, -1, 0), color = BLUE) + nmText = TextMobject(r'$r\prime\prime (t)$').next_to(nm, DOWN+RIGHT, buff = 0).scale(0.7) + nm2 = DashedLine((0,0,0),(2, -1, 0), color = GRAY).shift(2*UP + RIGHT) + square = Square(fill_color = WHITE, fill_opacity = 0.2).rotate(63*DEGREES).shift(0.5*UP +1.5*RIGHT).scale(1.1) + square.set_stroke(width = 0.1) + arrow = CurvedArrow(square.get_center() + np.array([2,1,0]), square.get_center() + np.array([0.5,0,0])) + arrowText = TextMobject(r'$r\prime (t)\times r\prime\prime (t)$').next_to(arrow.get_start(), DOWN+1*RIGHT, buff = 0).scale(0.7) + + text1 = TextMobject(r'$\left|\frac{dT}{ds}\right| = \frac{\left|\frac{dT}{dt}\right|}{\left|\frac{ds}{dt}\right|}$').shift(UP+3*LEFT) + text2 = TextMobject(r'$\left|\frac{dT}{ds}\right| = \frac{\frac{r\prime\prime (t)}{\left| r\prime (t)\right|}\times\frac{r\prime (t)}{\left| r\prime (t)\right|}}{\left|r\prime (t)\right|}$').next_to(text1, DOWN, buff = 0.1) + unit = VGroup(*[tgt, tgt2, nm, nm2]) + + # self.play(FadeIn(VGroup(*[tgt, tgt2, nm, nm2, nmText, tgtText, square, arrow, arrowText]))) + tgt2text = TextMobject(r'$\frac{r\prime (t)}{\left| r\prime (t)\right|}$').shift(1.1*UP).scale(0.7).rotate(63*DEGREES ) + nm2text = TextMobject(r'$\frac{r\prime\prime (t)}{\left| r\prime (t)\right|}$').scale(0.7).shift(0.7*RIGHT+0.8*DOWN).rotate(-25*DEGREES) + unit2 = unit.copy().scale(0.5).shift(0.75*LEFT+0.25*DOWN) + + self.play(FadeIn(VGroup(*[tgt, tgtText]))) + self.wait(1) + self.play(FadeIn(VGroup(*[nm, nmText]))) + self.wait(1) + self.play(FadeIn(VGroup(*[tgt2, nm2]))) + self.wait(1) + self.play(FadeIn(VGroup(*[square, arrow, arrowText]))) + self.wait(1) + self.play(FadeIn(unit2)) + self.wait(1) + self.play(FadeIn(VGroup(*[tgt2text, nm2text]))) + self.wait(1) + self.play(FadeIn(text1)) + self.wait(1) + self.play(FadeIn(text2)) + self.wait(2) + self.play(FadeOut(VGroup(*[tgt2text, nm2text, text1, text2, tgt, tgtText,nm, nmText,tgt2, nm2,square, arrow, arrowText,unit2]))) diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file3_curvature_intuition.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file3_curvature_intuition.gif Binary files differdeleted file mode 100644 index 0d6fdcf..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file3_curvature_intuition.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file4_different_curvature_single_curve.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file4_different_curvature_single_curve.gif Binary files differnew file mode 100644 index 0000000..3b78b5f --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file4_different_curvature_single_curve.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file4_different_curvature_single_curve.py b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file4_different_curvature_single_curve.py index d71adda..56b7fbb 100644 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file4_different_curvature_single_curve.py +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/arc-length-and-curvature/file4_different_curvature_single_curve.py @@ -8,7 +8,9 @@ class GR(GraphScene): "x_max": 6, "y_min": -6, "y_max": 10, - "graph_origin": ORIGIN + "graph_origin": ORIGIN, + 'x_tick_frequency': 20, + 'y_tick_frequency': 20 } def construct(self): @@ -21,7 +23,7 @@ class GR(GraphScene): tracker = ValueTracker(-3) - text = TextMobject(r'The curvature at point $P_{1}$ is \\ lesser than that at point $P_{2}$: \\ as $\kappa = \frac{1}{R}$').shift(3.2*RIGHT+3*UP).scale(0.6) + text = TextMobject(r'$\because R_{1} > R_{2}$, the curvature at \\ point $P_{1}$ is less than that \\ at point $P_{2}$ as $\kappa = \frac{1}{R}$').shift(3.2*RIGHT+3*UP).scale(0.6) dot1 = Dot((0,3,0), color = YELLOW) dot1label = TextMobject(r'$P_{1}$').next_to(dot1, UP+RIGHT, buff = 0.1) @@ -47,10 +49,30 @@ class GR(GraphScene): line.move_to(p0) return line + circle1 = Circle(radius = 0.8, color = GREY, opacity = 0.2).shift(2.2*UP) + tgt1 = Line((-2,3,0), (2,3,0), color = GREY, opacity = 0.2).scale(0.4) + + r1 = Line(circle1.get_center(), circle1.get_center() + np.array([0,0.8,0]), color=GREEN_SCREEN) + r1label = TextMobject(r'$R_{1}$',color=WHITE).next_to(r1, RIGHT, buff = 0.1).scale(0.6) + + curvature1 = VGroup(*[circle1, tgt1, r1, r1label]) + + circle2 = Circle(radius = 0.6, color = GREY, opacity = 0.2).shift(0.4*DOWN + 4*RIGHT) + tgt2 = Line((4,-2,0), (6, -2, 0), color = GREY, opacity = 0.2).scale(0.5).shift(LEFT + UP) + + r2 = Line(circle2.get_center(), circle2.get_center() + np.array([0,-0.6,0]), color=GREEN_SCREEN) + r2label = TextMobject(r'$R_{2}$', color=WHITE).next_to(r2, 0.9*RIGHT, buff = 0).scale(0.6) + + curvature2 = VGroup(*[circle2, tgt2, r2, r2label]) + line = always_redraw(get_tangent_line) self.add(graph,line, dots, text) self.wait(1.2) - self.play(tracker.set_value, 6, rate_func=smooth, run_time=13) - self.play(FadeOut(VGroup(*[graph, self.axes, line, dots, text]))) + self.play(tracker.set_value, 0, rate_func=smooth, run_time=5) + self.play(FadeIn(curvature1)) + self.play(tracker.set_value, 4, rate_func=smooth, run_time=5) + self.play(FadeIn(curvature2)) + self.play(tracker.set_value, 6, rate_func=smooth, run_time=3) + self.play(FadeOut(VGroup(*[curvature1, curvature2, graph, self.axes, line, dots, text]))) self.wait() diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/README.md b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/README.md new file mode 100644 index 0000000..29d2f6a --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/README.md @@ -0,0 +1,14 @@ +**file1_line_eqn.py**<br> + + +**file2_point_normal_form_plane.py**<br> + + +**file3_intercept_form_plane.py**<br> + + +**file4_3d_plane.py**<br> + + +**file5_vector_form_line.py**<br> + diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/__pycache__/file1_line_eqn.cpython-38.pyc b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/__pycache__/file1_line_eqn.cpython-38.pyc Binary files differdeleted file mode 100644 index e129d1d..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/__pycache__/file1_line_eqn.cpython-38.pyc +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/__pycache__/file4_point_normal_form_plane.cpython-38.pyc b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/__pycache__/file4_point_normal_form_plane.cpython-38.pyc Binary files differdeleted file mode 100644 index 88377bb..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/__pycache__/file4_point_normal_form_plane.cpython-38.pyc +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/file1_line_eqn.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/file1_line_eqn.gif Binary files differnew file mode 100644 index 0000000..a8a301a --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/file1_line_eqn.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/file2_point_normal_form_plane.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/file2_point_normal_form_plane.gif Binary files differnew file mode 100644 index 0000000..e651be0 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/file2_point_normal_form_plane.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/file5_vector_form_line.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/file5_vector_form_line.gif Binary files differnew file mode 100644 index 0000000..b6fdb51 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/equations-of-planes-and-lines/file5_vector_form_line.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/README.md b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/README.md new file mode 100644 index 0000000..8a47a0e --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/README.md @@ -0,0 +1,11 @@ +**file1_parametric_circle..py** <br> + + +**file2_cycloid_manim.py** <br> + + +**file3_brachistochrone.py** <br> + + +**file4_helix_visualization.py** <br> + diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/__pycache__/file1_parametric_circle.cpython-38.pyc b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/__pycache__/file1_parametric_circle.cpython-38.pyc Binary files differdeleted file mode 100644 index ad30b2a..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/__pycache__/file1_parametric_circle.cpython-38.pyc +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/__pycache__/file4_helix_visualization.cpython-38.pyc b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/__pycache__/file4_helix_visualization.cpython-38.pyc Binary files differdeleted file mode 100644 index 144d78d..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/__pycache__/file4_helix_visualization.cpython-38.pyc +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file1_parametric_circle.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file1_parametric_circle.gif Binary files differnew file mode 100644 index 0000000..732b6bb --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file1_parametric_circle.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file1_parametric_circle.py b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file1_parametric_circle.py index 40b5150..37d079e 100644 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file1_parametric_circle.py +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file1_parametric_circle.py @@ -11,12 +11,15 @@ class parametricCircle(ThreeDScene, GraphScene): self.y_axis_label = "" self.x_axis_width = 10 self.y_axis_height = 10 + self.y_tick_frequency = 1.9 + self.x_tick_frequency = 1.4 axes = [] - self.setup_axes() - self.axes.scale(0.5).shift(3*LEFT) - axes.append(self.axes) + # self.setup_axes() + ax = Axes(y_tick_frequency = 1, x_axis_width = 10, y_axis_height = 10, y_min = -5, x_max = 5, y_max = 5, x_tick_frequency = 1, x_axis_label = "", y_axis_label = "", x_min = -5, ) + ax.scale(0.5).shift(3*LEFT) + axes.append(ax) self.setup_axes() self.axes.scale(0.3).shift(3*RIGHT + 2*UP) axes.append(self.axes) @@ -38,7 +41,7 @@ class parametricCircle(ThreeDScene, GraphScene): asint = ParametricFunction( lambda t: np.array([ t, - np.sin(t), + 2*np.sin(t), 0 ]), t_min = -np.pi, t_max = np.pi, color = GREEN_E ).shift(3*RIGHT + 2*UP).scale(0.4) @@ -50,7 +53,7 @@ class parametricCircle(ThreeDScene, GraphScene): acost = ParametricFunction( lambda t: np.array([ t, - np.cos(t), + 2*np.cos(t), 0 ]), t_min = -np.pi, t_max = np.pi, color = BLUE ).shift(3*RIGHT + 2*DOWN).scale(0.4) diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file2_cycloid.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file2_cycloid.gif Binary files differdeleted file mode 100644 index 39656de..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file2_cycloid.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file4_helix_visualization.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file4_helix_visualization.gif Binary files differnew file mode 100644 index 0000000..16d2509 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/general-parametric-curves/file4_helix_visualization.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/README.md b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/README.md new file mode 100644 index 0000000..42f5df1 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/README.md @@ -0,0 +1,11 @@ +**file1_parametric_ellipse.py** <br> + + +**file2_parametric_helix.py** <br> + + +**file3_circletosphere.py** <br> + + +**file4_cone.py** <br> + diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file1_parametric_ellipse.cpython-38.pyc b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file1_parametric_ellipse.cpython-38.pyc Binary files differdeleted file mode 100644 index a732643..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file1_parametric_ellipse.cpython-38.pyc +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file2_parametric_helix.cpython-38.pyc b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file2_parametric_helix.cpython-38.pyc Binary files differdeleted file mode 100644 index c8e3e2a..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file2_parametric_helix.cpython-38.pyc +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file3_circletosphere.cpython-38.pyc b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file3_circletosphere.cpython-38.pyc Binary files differdeleted file mode 100644 index bca0d91..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file3_circletosphere.cpython-38.pyc +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file3_cone.cpython-38.pyc b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file3_cone.cpython-38.pyc Binary files differdeleted file mode 100644 index ae954c3..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/__pycache__/file3_cone.cpython-38.pyc +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file1_parametric_ellipse.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file1_parametric_ellipse.gif Binary files differnew file mode 100644 index 0000000..90c0349 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file1_parametric_ellipse.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file2_parametric_helix.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file2_parametric_helix.gif Binary files differnew file mode 100644 index 0000000..4f349b1 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file2_parametric_helix.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file3_circletosphere.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file3_circletosphere.gif Binary files differnew file mode 100644 index 0000000..d6a8afc --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file3_circletosphere.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file4_cone.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file4_cone.gif Binary files differnew file mode 100644 index 0000000..b126d20 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/space-curves/file4_cone.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/README.md b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/README.md new file mode 100644 index 0000000..7874f43 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/README.md @@ -0,0 +1,15 @@ +**file1_tnb_creation.py**<br> + + + +**file2_tnb_basic.py** <br> + + +**file3_tnb_frame_manim.py** <br> + + +**file4_fs1.py** <br> + + +**file5_fs2.py** <br> + diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file1_prescribed_plane.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file1_prescribed_plane.gif Binary files differdeleted file mode 100644 index c8668e3..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file1_prescribed_plane.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file1_tnb_creation.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file1_tnb_creation.gif Binary files differnew file mode 100644 index 0000000..eae8686 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file1_tnb_creation.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file1_tnb_creation.py b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file1_tnb_creation.py new file mode 100644 index 0000000..80372ee --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file1_tnb_creation.py @@ -0,0 +1,66 @@ +from manimlib.imports import * + +class tnb(ThreeDScene): + def construct(self): + self.set_camera_orientation(phi = 75*DEGREES, theta=45*DEGREES) + + helix1 = ParametricFunction( + lambda t: np.array([ + np.cos(TAU*t), + np.sin(TAU*t), + 0.4*t + ]), t_min = -2*np.pi/3, t_max = -1.638*np.pi/3, color = WHITE + ) + + helix2 = ParametricFunction( + lambda t: np.array([ + np.cos(TAU*t), + np.sin(TAU*t), + 0.4*t + ]), t_min = -1.638*np.pi/3, t_max = -1.33*np.pi/3, color = WHITE + ) + + pointText = TextMobject(r'Consider an arbitrary point \\ on the given curve.').scale(0.8).shift(1.5*UP) + tgtText = TextMobject(r'Unit', ' tangent ', r'vector at \\ this point is given as:').scale(0.8).shift(1.5*UP) + tgtText.set_color_by_tex_to_color_map({ + "tangent": YELLOW + }) + normalText = TextMobject(r'Unit', ' normal ', r'vector at \\ this point is given as:').scale(0.8).shift(1.5*UP) + normalText.set_color_by_tex_to_color_map({ + "normal": BLUE + }) + planeText = TextMobject(r'$\overrightarrow{T}$ and $\overrightarrow{N}$ \\ prescribe a plane.').scale(0.8).shift(1.5*UP) + bnmText = TextMobject(r'The vector normal to this plane \\ is called the', ' binormal ', 'vector.').scale(0.8).shift(1.5*UP) + bnmText.set_color_by_tex_to_color_map({ + "binormal": GREEN_E + }) + + dot1 = Dot(np.array([np.cos(-np.pi/3), np.sin(-np.pi/3), -0.4*np.pi/3]) + np.array([0,0.2,0]), radius = 0.16, color=RED) + tgt1 = Arrow((0,0,0), (-2,-0.55,0), color = YELLOW).shift(dot1.get_center() + np.array([0.18,0.04,0])) + nm1 = Arrow((0,0,0), (0.4,-2,0), color = BLUE).shift(dot1.get_center() + np.array([0,0.26,0])) + bnm1 = Arrow((0,0,0), (0,2,0), color=GREEN_E).shift(2.1*RIGHT+2*DOWN) + plane1 = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).shift(dot1.get_center() + np.array([-0.4, -0.6, 0])).rotate(13*DEGREES).scale(1.2) + point1 = VGroup(*[dot1, tgt1, nm1, plane1]).scale(0.8).shift(np.array([1,4.86,0])).rotate(-15*DEGREES) + + + + helix = VGroup(*[helix1, helix2]) + self.play(FadeIn(helix)) + self.play(ApplyMethod(helix.scale, 4)) + self.add_fixed_in_frame_mobjects(pointText) + self.play(FadeIn(dot1), FadeIn(pointText)) + self.wait(2) + self.add_fixed_in_frame_mobjects(tgtText) + self.play(Write(tgt1), ReplacementTransform(pointText, tgtText)) + self.wait(2) + self.add_fixed_in_frame_mobjects(normalText) + self.play(Write(nm1), ReplacementTransform(tgtText, normalText)) + self.wait(2) + self.add_fixed_in_frame_mobjects(planeText) + self.play(FadeIn(plane1), ReplacementTransform(normalText, planeText)) + self.wait(2) + self.add_fixed_in_frame_mobjects(bnmText) + self.add_fixed_in_frame_mobjects(bnm1) + self.play(ReplacementTransform(planeText, bnmText), Write(bnm1)) + self.wait(2) + self.play(FadeOut(VGroup(*[helix, bnm1, bnmText, dot1, tgt1, nm1, plane1]))) diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file2_TNB_frame.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file2_TNB_frame.gif Binary files differdeleted file mode 100644 index 097652f..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file2_TNB_frame.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file2_tnb_basic.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file2_tnb_basic.gif Binary files differnew file mode 100644 index 0000000..67aaea2 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file2_tnb_basic.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file2_tnb_basic.py b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file2_tnb_basic.py new file mode 100644 index 0000000..c870210 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file2_tnb_basic.py @@ -0,0 +1,36 @@ +from manimlib.imports import * + +class tnb(ThreeDScene): + def construct(self): + t = TextMobject(r'T', color = YELLOW) + n = TextMobject(r'N', color = BLUE).next_to(t, RIGHT, buff=0) + b = TextMobject(r'B', color = GREEN_E).next_to(n, RIGHT, buff=0) + frame = TextMobject(r'Frame').next_to(b, RIGHT, buff=0.2) + f1 = TextMobject(r'$\overrightarrow{B}$ ', color = GREEN_E) + f2 = TextMobject(r' = $\overrightarrow{T}$', color = YELLOW).next_to(f1, RIGHT, buff=0.2) + f3 = TextMobject(r'$\times\overrightarrow{N}$', color = BLUE).next_to(f2, RIGHT, buff=0.1) + formula = VGroup(*[f1, f2, f3]).move_to(ORIGIN).shift(3*UP) + + # text = VGroup(*[t,n,b,frame]).move_to(ORIGIN).shift(3*UP) + curve = ParametricFunction( + lambda t: np.array([ + np.sin(TAU*t), + np.cos(TAU*t), + 0 + ]) + ).scale(2.5) + dot = Dot(color = RED).scale(1.5).shift(1.05*LEFT) + tgt = Arrow(dot.get_center(), (-2, 2, 0), color = YELLOW).shift(0.3*DOWN + 0.09*RIGHT) + normal = Arrow(tgt.get_start(), (1, 1, 0), color = BLUE).shift(0.2*LEFT + 0.05*DOWN) + binormal = Arrow(dot.get_center() - np.array([0,0,0.3]), (tgt.get_start()[0], tgt.get_start()[1],2), color = GREEN) + square = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).move_to(tgt.get_start()).rotate(27*DEGREES).shift(UP+0.4*RIGHT).scale(1.2) + group = VGroup(*[dot, tgt, normal, square, binormal]).shift(np.array([-1.24,-1,0])) + + self.add_fixed_in_frame_mobjects(formula) + self.add(curve, group) + self.wait(1) + self.move_camera(phi = 75*DEGREES, theta=45*DEGREES, run_time = 2) + self.add_fixed_in_frame_mobjects(formula) + self.begin_ambient_camera_rotation(rate = 0.5) + self.wait(5) + self.play(FadeOut(VGroup(*[formula, curve, dot, tgt, normal, square, binormal]))) diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file3_tnb_frame_manim.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file3_tnb_frame_manim.gif Binary files differnew file mode 100644 index 0000000..78e3aa3 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file3_tnb_frame_manim.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file3_tnb_frame_manim.py b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file3_tnb_frame_manim.py new file mode 100644 index 0000000..176cac5 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file3_tnb_frame_manim.py @@ -0,0 +1,126 @@ +from manimlib.imports import * + +class tnb(ThreeDScene): + def construct(self): + self.set_camera_orientation(phi = 75*DEGREES, theta=45*DEGREES) + + t = TextMobject(r'T', color = YELLOW) + n = TextMobject(r'N', color = BLUE).next_to(t, RIGHT, buff=0) + b = TextMobject(r'B', color = GREEN_E).next_to(n, RIGHT, buff=0) + frame = TextMobject(r'Frame').next_to(b, RIGHT, buff=0.2) + + text = VGroup(*[t,n,b,frame]).move_to(ORIGIN).shift(3*UP) + + helix1 = ParametricFunction( + lambda t: np.array([ + np.cos(TAU*t), + np.sin(TAU*t), + 0.4*t + ]), t_min = -2*np.pi/3, t_max = -1.638*np.pi/3, color = WHITE + ) + + helix2 = ParametricFunction( + lambda t: np.array([ + np.cos(TAU*t), + np.sin(TAU*t), + 0.4*t + ]), t_min = -1.638*np.pi/3, t_max = -1.33*np.pi/3, color = WHITE + ) + + helix3 = ParametricFunction( + lambda t: np.array([ + np.cos(TAU*t), + np.sin(TAU*t), + 0.4*t + ]), t_min = -1.33*np.pi/3, t_max = -np.pi/3, color = WHITE + ) + + helix4 = ParametricFunction( + lambda t: np.array([ + np.cos(TAU*t), + np.sin(TAU*t), + 0.4*t + ]), t_min = -np.pi/3, t_max = -1.3*np.pi/6, color = WHITE + ) + + helix5 = ParametricFunction( + lambda t: np.array([ + np.cos(TAU*t), + np.sin(TAU*t), + 0.4*t + ]), t_min = -1.3*np.pi/6, t_max = 0, color = WHITE + ) + + helix_dot = Dot(radius = 0.16, color = RED) + + dot0 = Dot(np.array([np.cos(-2*np.pi/3), np.sin(-2*np.pi/3), -0.8*np.pi/3]), radius = 0.16, color=RED).shift(np.array([4.65,0,-0.8])) + tgt0 = Arrow((0,0,0), (1,2,0), color = YELLOW).shift(dot0.get_center() - np.array([0.04,0.2,0])) + nm0 = Arrow((0,0,0), (-2,1,0), color = BLUE).shift(dot0.get_center() + np.array([0.3,0,0])) + bnm0 = Arrow((0,0,0), (0,2,0), color = GREEN_E).shift(6.1*LEFT + 3*DOWN) + plane0 = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).shift(dot0.get_center() + np.array([-0.35, 0.85, 0])).scale(1.2).rotate(65*DEGREES) + point0 = VGroup(*[dot0, tgt0, nm0, bnm0, plane0]).scale(0.8).shift(np.array([1,0,0])) + + dot1 = Dot(np.array([np.cos(-np.pi/3), np.sin(-np.pi/3), -0.4*np.pi/3]) + np.array([0,0.2,0]), radius = 0.16, color=RED) + tgt1 = Arrow((0,0,0), (-2,-0.55,0), color = YELLOW).shift(dot1.get_center() + np.array([0.18,0.04,0])) + nm1 = Arrow((0,0,0), (0.4,-2,0), color = BLUE).shift(dot1.get_center() + np.array([0,0.26,0])) + bnm1 = Arrow((0,0,0), (0,2,0), color=GREEN_E).shift(3.68*RIGHT+2.48*DOWN) + plane1 = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).shift(dot1.get_center() + np.array([-0.4, -0.6, 0])).rotate(13*DEGREES).scale(1.2) + point1 = VGroup(*[dot1, tgt1, nm1, plane1]).scale(0.8).shift(np.array([1,6.25,0])) + + dot2 = Dot(np.array([np.cos(-np.pi/6), np.sin(-np.pi/6), -0.2*np.pi/3]) - np.array([1.9,0,0]), radius=0.16,color=RED) + tgt2 = Arrow((0,0,0), (1,-2,0), color = YELLOW).shift(dot2.get_center() + np.array([-0.2,0.2,0])) + nm2 = Arrow((0,0,0), (2,1,0), color = BLUE).shift(dot2.get_center() + np.array([-0.2,-0.06,0])) + bnm2 = Arrow((0,0,0), (0,2,0), color=GREEN_E).shift(0.4*RIGHT + 0.16*DOWN) + plane2 = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).shift(dot2.get_center() + np.array([0.92, -0.5, 0])).rotate(23*DEGREES).scale(1.2) + point2 = VGroup(*[dot2, tgt2, nm2, bnm2, plane2]) + + helix = VGroup(*[helix1, helix2, helix3, helix4, helix5]) + self.add_fixed_in_frame_mobjects(text) + self.play(FadeIn(helix), FadeIn(text)) + self.play(ApplyMethod(helix.scale, 4)) + self.add_fixed_in_frame_mobjects(bnm0) + self.play(FadeIn(point0)) + self.play(ApplyMethod(point0.set_color, GRAY, opacity = 0.1), MoveAlongPath(helix_dot, helix1, run_time=5)) + + self.add_fixed_in_frame_mobjects(bnm1) + self.play(FadeIn(point1)) + self.play(ApplyMethod(point1.set_color, GRAY, opacity = 0.1), ApplyMethod(bnm1.set_color, GRAY, opacity = 0.1), MoveAlongPath(helix_dot, helix2, run_time = 5)) + + self.add_fixed_in_frame_mobjects(bnm2) + self.play(FadeIn(point2)) + self.play(ApplyMethod(point2.set_color, GRAY, opacity = 0.1), MoveAlongPath(helix_dot, helix3, run_time=5)) + + dot3 = Dot(np.array([np.cos(-np.pi/3), np.sin(-np.pi/3), -0.4*np.pi/3]) + np.array([3.3,-0.25,0]), radius = 0.16, color=RED) + tgt3 = Arrow((0,0,0), (0,2,0), color = YELLOW).shift(helix_dot.get_center() - np.array([-0.05,0.2,0])) + nm3 = Arrow((0,0,0), (-2,0,0), color = BLUE).shift(helix_dot.get_center() + np.array([0.25,0,0])) + bnm3 = Arrow((0,0,0), (0,2,0), color = GREEN_E).shift(3.87*LEFT + 1.24*DOWN) + plane3 = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).shift(helix_dot.get_center() + np.array([-0.5, 0.62, 0])) + point3 = VGroup(*[dot3, tgt3, nm3, bnm3, plane3]).shift(np.array([0,0,0])) + + dot4 = Dot(np.array([np.cos(-np.pi/12), np.sin(-np.pi/12), -0.1*np.pi/3]) + np.array([-3.4,3.4,0]), radius = 0.16, color=RED) + tgt4 = Arrow((0,0,0), (-2,-0.85,0), color = YELLOW).shift(dot4.get_center() - np.array([-0.05,0,0])) + nm4 = Arrow((0,0,0), (0.8,-2,0), color = BLUE).shift(dot4.get_center() + np.array([-0.1,0.25,0])) + bnm4 = Arrow((0,0,0), (0,2,0), color = GREEN_E).shift(4.03*RIGHT + 0.5*DOWN) + plane4 = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).shift(dot4.get_center() + np.array([-0.4,-1,0])).rotate(22*DEGREES).scale(1.2) + point4 = VGroup(*[dot4, tgt4, nm4, bnm4, plane4]) + + dot5 = Dot((1,0,0) + np.array([2.3,-1,1])) + tgt5 = Arrow((0,0,0), (0,2,0), color = YELLOW).shift(dot5.get_center() - np.array([-0.05,0.2,0])) + nm5 = Arrow((0,0,0), (-2,0,0), color = BLUE).shift(dot5.get_center() + np.array([0.25,0,0])) + bnm5 = Arrow((0,0,0), (0,2,0), color = GREEN_E).shift(3.34*LEFT+0.3*UP) + plane5 = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).shift(dot5.get_center() + np.array([-0.5,0.5,0])) + point5 = VGroup(*[tgt5, nm5, bnm5, plane5]) + + self.add_fixed_in_frame_mobjects(bnm3) + self.play(FadeIn(point3)) + self.play(ApplyMethod(point3.set_color, GRAY, opacity = 0.1), MoveAlongPath(helix_dot, helix4, run_time=5)) + + self.add_fixed_in_frame_mobjects(bnm4) + self.play(FadeIn(point4)) + self.play(ApplyMethod(point4.set_color, GRAY, opacity = 0.1), MoveAlongPath(helix_dot, helix5, run_time=5)) + + self.add_fixed_in_frame_mobjects(bnm5) + self.play(FadeIn(point5)) + self.wait(2) + + self.play(FadeOut(VGroup(*[text, helix, bnm1, point0, point1, point2, point3, point4, point5, helix_dot]))) diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file4_fs1.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file4_fs1.gif Binary files differnew file mode 100644 index 0000000..6b4b438 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file4_fs1.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file4_fs1.py b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file4_fs1.py new file mode 100644 index 0000000..c719a1d --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file4_fs1.py @@ -0,0 +1,23 @@ +from manimlib.imports import * + +class fs1(ThreeDScene): + def construct(self): + + + self.set_camera_orientation(phi = 75*DEGREES, theta=45*DEGREES) + dot1 = Dot(np.array([np.cos(-np.pi/3), np.sin(-np.pi/3), -0.4*np.pi/3]) + np.array([0,0.2,0]), radius = 0.16, color=RED) + tgt1 = Arrow((0,0,0), (-2,-0.55,0), color = YELLOW).shift(dot1.get_center() + np.array([0.18,0.04,0])) + nm1 = Arrow((0,0,0), (0.4,-2,0), color = BLUE).shift(dot1.get_center() + np.array([0,0.26,0])).shift(np.array([0.8,4.76,0])).rotate(-15*DEGREES).scale(0.8) + bnm1 = Arrow((0,0,0), (0,2,0), color=GREEN_E).shift(2.1*RIGHT+2*DOWN) + plane1 = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).shift(dot1.get_center() + np.array([-0.4, -0.6, 0])).rotate(13*DEGREES).scale(1.2) + point1 = VGroup(*[dot1, tgt1, plane1]).scale(0.8).shift(np.array([1,4.86,0])).rotate(-15*DEGREES) + t = TextMobject(r'$T$', color = YELLOW).move_to(ORIGIN).shift(3.2*RIGHT + DOWN) + n = TextMobject(r'$N$', color = BLUE).shift(DOWN + RIGHT) + b = TextMobject(r'$B$', color = GREEN_E).next_to(bnm1, UP, buff = 0.1) + text = VGroup(*[t, n, b]) + self.add_fixed_in_frame_mobjects(bnm1, text) + self.play(FadeIn(point1), FadeIn(bnm1), FadeIn(text)) + self.wait() + self.play(TransformFromCopy(tgt1, nm1, run_time = 2)) + self.wait(2) + self.play(FadeOut(VGroup(*[bnm1, text, point1, nm1]))) diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file5_fs2.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file5_fs2.gif Binary files differnew file mode 100644 index 0000000..ce367b6 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file5_fs2.gif diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file5_fs2.py b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file5_fs2.py new file mode 100644 index 0000000..0261fed --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/tnb-frame-and-serret-frenet-formulae/file5_fs2.py @@ -0,0 +1,28 @@ +from manimlib.imports import * + +class fs1(ThreeDScene): + def construct(self): + + + self.set_camera_orientation(phi = 75*DEGREES, theta=45*DEGREES) + dot1 = Dot(np.array([np.cos(-np.pi/3), np.sin(-np.pi/3), -0.4*np.pi/3]) + np.array([0,0.2,0]), radius = 0.16, color=RED) + tgt1 = Arrow((0,0,0), (-2,-0.55,0), color = YELLOW).shift(dot1.get_center() + np.array([0.18,0.04,0])) + nm1 = Arrow((0,0,0), (0.4,-2,0), color = BLUE).shift(dot1.get_center() + np.array([0,0.26,0])).shift(np.array([0.8,4.76,0])).rotate(-15*DEGREES).scale(0.8) + bnm1 = Arrow((0,0,0), (0,2,0), color=GREEN_E).shift(2.1*RIGHT+2*DOWN) + + bnms = Line((0,0,0), (0,0,1.6), color = GREEN_E).shift(np.array([3.1,5.2,0])).scale(0.6) + bnmsa = ArrowTip(color = GREEN_E).next_to(bnms, np.array([0,0,1]), buff = 0).rotate(45*DEGREES) + bns = VGroup(*[bnms, bnmsa]) + + plane1 = Square(color = DARK_BROWN, fill_color = WHITE, fill_opacity=0.3).shift(dot1.get_center() + np.array([-0.4, -0.6, 0])).rotate(13*DEGREES).scale(1.2) + point1 = VGroup(*[dot1, tgt1, plane1]).scale(0.8).shift(np.array([1,4.86,0])).rotate(-15*DEGREES) + t = TextMobject(r'$T$', color = YELLOW).move_to(ORIGIN).shift(3.2*RIGHT + DOWN) + n = TextMobject(r'$N$', color = BLUE).shift(DOWN + RIGHT) + b = TextMobject(r'$B$', color = GREEN_E).next_to(bnm1, UP, buff = 0.1) + text = VGroup(*[t, n, b]) + self.add_fixed_in_frame_mobjects(bnm1, text) + self.play(FadeIn(point1), FadeIn(text), FadeIn(bnm1)) + self.wait() + self.play(TransformFromCopy(bnms, nm1, run_time = 3)) + self.wait(2) + self.play(FadeOut(VGroup(*[bnms, text, point1, nm1, bnm1]))) diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/velocity-and-differentiability/README.md b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/velocity-and-differentiability/README.md new file mode 100644 index 0000000..bc571c6 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/velocity-and-differentiability/README.md @@ -0,0 +1,2 @@ +**file2_tangent_space_curve.py** <br> + diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/velocity-and-differentiability/__pycache__/file2_tangent_spaceCurve.cpython-38.pyc b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/velocity-and-differentiability/__pycache__/file2_tangent_spaceCurve.cpython-38.pyc Binary files differdeleted file mode 100644 index 8967b87..0000000 --- a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/velocity-and-differentiability/__pycache__/file2_tangent_spaceCurve.cpython-38.pyc +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/velocity-and-differentiability/file2_tangent_space_curve.gif b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/velocity-and-differentiability/file2_tangent_space_curve.gif Binary files differnew file mode 100644 index 0000000..06ed70f --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/geometry-of-planes-and-curves/velocity-and-differentiability/file2_tangent_space_curve.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Limits and Continuity of Multivariable Functions/gifs/limit_approach_point.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Limits and Continuity of Multivariable Functions/gifs/limit_approach_point.gif Binary files differdeleted file mode 100644 index 830b6f1..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Limits and Continuity of Multivariable Functions/gifs/limit_approach_point.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_derivative_vectorvf.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_derivative_vectorvf.gif Binary files differdeleted file mode 100644 index a94de90..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_derivative_vectorvf.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_examples.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_examples.gif Binary files differdeleted file mode 100644 index 11f66f1..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_examples.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_plot_sphere.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_plot_sphere.gif Binary files differdeleted file mode 100644 index ad7582c..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_plot_sphere.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_respresntation.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_respresntation.gif Binary files differdeleted file mode 100644 index a173bda..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_respresntation.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_vectorvf_sine.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_vectorvf_sine.gif Binary files differdeleted file mode 100644 index 4f6b931..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/gifs/multivariable_func_vectorvf_sine.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_examples.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_examples.py deleted file mode 100644 index 7322e47..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_examples.py +++ /dev/null @@ -1,69 +0,0 @@ -from manimlib.imports import *
-
-class Examples(GraphScene):
- def construct(self):
-
- rectangle = Rectangle(height = 3, width = 4, color = GREEN)
- square = Square(side_length = 5, color = PURPLE)
- circle = Circle(radius = 2, color = PINK)
- radius = Line(ORIGIN,2*RIGHT)
-
- radius.set_color(RED)
-
- rectangle_area_func = TextMobject(r"$Area = f(Length, Breadth)$")
- rectangle_area_func.scale(0.6)
- square_area_func = TextMobject(r"$Area = f(Length)$")
- circle_area_func = TextMobject(r"$Area = f(r)$")
-
-
- rectangle_area = TextMobject(r"$Area = Length \times Breadth$")
- rectangle_area.scale(0.6)
- square_area = TextMobject(r"$Area = Length^2$")
- circle_area = TextMobject(r"$Area = \pi r^2$")
-
- braces_rect1 = Brace(rectangle, LEFT)
- eq_text1 = braces_rect1.get_text("Length")
- braces_rect2 = Brace(rectangle, UP)
- eq_text2 = braces_rect2.get_text("Breadth")
-
- braces_square = Brace(square, LEFT)
- braces_square_text = braces_square.get_text("Length")
-
- radius_text = TextMobject("r")
- radius_text.next_to(radius,UP)
-
-
-
- self.play(ShowCreation(rectangle))
- self.wait(1)
- self.play(GrowFromCenter(braces_rect1),Write(eq_text1),GrowFromCenter(braces_rect2),Write(eq_text2))
- self.wait(1)
- self.play(Write(rectangle_area_func))
- self.wait(1)
- self.play(Transform(rectangle_area_func, rectangle_area))
- self.wait(1)
- self.play(FadeOut(braces_rect1),FadeOut(eq_text1),FadeOut(braces_rect2),FadeOut(eq_text2),FadeOut(rectangle_area_func))
-
-
- self.play(Transform(rectangle, square))
- self.wait(1)
- self.play(GrowFromCenter(braces_square),Write(braces_square_text))
- self.wait(1)
- self.play(Write(square_area_func))
- self.wait(1)
- self.play(Transform(square_area_func, square_area))
- self.wait(1)
- self.play(FadeOut(braces_square),FadeOut(braces_square_text),FadeOut(square_area_func))
-
-
- self.play(Transform(rectangle, circle))
- self.wait(1)
- self.play(ShowCreation(radius),Write(radius_text))
- self.wait(1)
- self.play(FadeOut(radius_text),FadeOut(radius))
- self.wait(1)
- self.play(Write(circle_area_func))
- self.wait(1)
- self.play(Transform(circle_area_func, circle_area))
- self.wait(1)
- self.play(FadeOut(circle_area_func))
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_plot_sphere.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_plot_sphere.py deleted file mode 100644 index baf08b1..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_plot_sphere.py +++ /dev/null @@ -1,42 +0,0 @@ -from manimlib.imports import *
-
-class Sphere(ThreeDScene):
- def construct(self):
- axes = ThreeDAxes() # creates a 3D Axis
-
- sphere = ParametricSurface(
- lambda u, v: np.array([
- np.sin(u)*np.cos(v),
- np.sin(u)*np.sin(v),
- np.cos(u)
- ]),u_min=0,u_max=PI,v_min=0,v_max=2*PI,checkerboard_colors=[RED_D, RED_E],
- resolution=(15, 32)).scale(2)
-
-
-
- #self.set_camera_orientation(phi=0 * DEGREES,theta=270*DEGREES)
-
- text3d = TextMobject(r"$f(x,y) \rightarrow Point(x,y,z)$")
- text3d1 = TextMobject(r"$f(x,y) \rightarrow Point(x,y, 1 - x^2 - y^2)$")
- self.add_fixed_in_frame_mobjects(text3d)
- text3d.scale(0.7)
- text3d1.scale(0.7)
- text3d.to_corner(UL)
- text3d1.to_corner(UL)
- text3d.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
- text3d1.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
- self.play(Write(text3d))
- self.wait(1)
-
- self.play(Transform(text3d,text3d1))
- self.add_fixed_in_frame_mobjects(text3d1)
- self.play(FadeOut(text3d))
-
-
- self.set_camera_orientation(phi=75 * DEGREES)
- self.begin_ambient_camera_rotation(rate=0.3)
-
-
- self.add(axes)
- self.play(Write(sphere))
- self.wait(5)
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_respresntation.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_respresntation.py deleted file mode 100644 index 4bfcf21..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_respresntation.py +++ /dev/null @@ -1,80 +0,0 @@ -from manimlib.imports import *
-
-class MultivariableFunc(Scene):
- def construct(self):
-
- topic = TextMobject("Multivariable Functions")
- topic.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
- topic.scale(2)
-
- self.play(Write(topic))
- self.wait(1)
- self.play(FadeOut(topic))
-
-
- circle = Circle()
- circle.scale(3)
-
- eqn1 = TextMobject(r"f(x,y) = $x^2y$")
- eqn1.set_color(YELLOW)
-
-
-
- number1 = TextMobject("(2,1)")
- number1.move_to(3*UP+ 3*LEFT)
- number1.scale(1.2)
- number1.set_color(GREEN)
-
- output1 = TextMobject("4")
- output1.scale(1.5)
- output1.set_color(BLUE)
-
- eqn1_1 = TextMobject(r"f(2,1) = $2^2(1)$")
- eqn1_1.set_color(YELLOW)
-
-
- self.play(ShowCreation(circle),Write(eqn1))
- self.wait(1)
- self.play(ApplyMethod(number1.move_to, 0.6*LEFT))
- self.play(FadeOut(number1))
- self.play(Transform(eqn1, eqn1_1))
- self.wait(1)
- self.play(ApplyMethod(output1.move_to, 3*DOWN+4*RIGHT))
- self.wait(1)
- self.play(FadeOut(output1))
-
-
- eqn2 = TextMobject(r"f(x,y,z) = $x^2y+2yz$")
- eqn2.set_color(YELLOW)
-
- number2 = TextMobject("(2,1,3)")
- number2.move_to(3*UP+ 3*LEFT)
- number2.scale(1.2)
- number2.set_color(GREEN)
-
- output2 = TextMobject("8")
- output2.scale(1.5)
- output2.set_color(BLUE)
-
- eqn2_1 = TextMobject(r"f(2,1,3) = $2^2(1) + 2(1)(3)$")
- eqn2_1.set_color(YELLOW)
-
- eqn2_2 = TextMobject(r"f(2,1,3) = $2 + 6$")
- eqn2_2.set_color(YELLOW)
-
-
-
- self.play(FadeOut(eqn1))
- self.play(Write(eqn2))
-
- self.wait(1)
- self.play(ApplyMethod(number2.move_to, 1.2*LEFT))
- self.play(FadeOut(number2))
- self.play(Transform(eqn2, eqn2_1))
- self.wait(1)
- self.play(Transform(eqn2, eqn2_2))
- self.wait(1)
- self.play(ApplyMethod(output2.move_to, 3*DOWN+4*RIGHT))
- self.wait(1)
- self.play(FadeOut(output2),FadeOut(eqn2),FadeOut(circle))
- self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/README.md b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/README.md index b50200d..97a0fb7 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/README.md +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/README.md @@ -4,6 +4,6 @@ Github Account : <a href="https://github.com/nishanpoojary">nishanpoojary</a> ## Sub-Topics Covered:
+ Scalar Functions
+ Multivariable Functions
-+ Limits and continuity of Multivariable Function
++ Multivariable Limits and Continuity
+ Partial Derivatives
+ Directonal Derivatives
diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/domain_range.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/domain_range.gif Binary files differdeleted file mode 100644 index d0351e5..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/domain_range.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_application.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_application.gif Binary files differdeleted file mode 100644 index 831ec8e..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_application.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_level_curves.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_level_curves.gif Binary files differdeleted file mode 100644 index 2df2fde..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_level_curves.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_level_curves2.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_level_curves2.gif Binary files differdeleted file mode 100644 index 724c27d..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_level_curves2.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_neural_nets.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_neural_nets.gif Binary files differdeleted file mode 100644 index 9d24688..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_neural_nets.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_parabola_example.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_parabola_example.gif Binary files differdeleted file mode 100644 index 3fdecf4..0000000 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/gifs/scalar_function_parabola_example.gif +++ /dev/null diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/README.md b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/README.md new file mode 100644 index 0000000..a62369d --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/README.md @@ -0,0 +1,8 @@ +**file1_directional_deriv** + + +**file2_gradient** + + +**file3_gradient_level_curves** + diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/file1_directional_deriv.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/file1_directional_deriv.py new file mode 100644 index 0000000..677d821 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/file1_directional_deriv.py @@ -0,0 +1,85 @@ +from manimlib.imports import *
+
+class GeomRepresen(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ paraboloid = ParametricSurface(
+ lambda u, v: np.array([
+ 3*np.sin(u)*np.cos(v),
+ 3*np.sin(u)*np.sin(v),
+ -0.25*3*3*np.sin(u)*np.sin(u)+2
+ ]),u_min=0,u_max=PI/4,v_min=0,v_max=2*PI, color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.7,
+ resolution=(15, 32)).scale(1)
+
+ parabola_curve = ParametricFunction(
+ lambda u : np.array([
+ u,
+ -u,
+ -0.5*(u*u)+2
+ ]),color=PINK,t_min=-1.5,t_max=1.5,
+ )
+
+ circle = Circle(radius = 2.22 , color = BLACK, fill_color = BLUE_C, fill_opacity= 0.3, stroke_width=0.1)
+
+ plane = Polygon(np.array([2.5,-2.5,0]),np.array([-2.5,2.5,0]),np.array([-2.5,2.5,2.5]),np.array([2.5,-2.5,2.5]),np.array([2.5,-2.5,0]), color = BLACK, fill_color = PINK, fill_opacity= 0.2, stroke_width=0.1)
+
+ line = DashedLine(np.array([1,-1,0]), np.array([1,-1,1.5]), color = YELLOW_C)
+
+ tangent_line = Line(np.array([1.5,-1.5,1]), np.array([0.5,-0.5,2]), color = RED_C)
+
+ vector = Arrow(np.array([1,-1,0]), np.array([0.5,-0.5,0]), buff=0.01, color = GREEN_C)
+
+ dot1 =Sphere(radius=0.08).move_to(np.array([1,-1,0])).set_fill(YELLOW_C)
+ dot2 =Sphere(radius=0.08).move_to(np.array([1,-1,1.5])).set_fill(YELLOW_C)
+
+ dot1_lab = TextMobject(r"$P_0$").scale(0.6).move_to(np.array([1,-1,1.8])).set_color(RED_C)
+ dot2_lab = TextMobject(r"$(x_0,y_0)$").scale(0.6).move_to(np.array([1.6,-1,0])).set_color(PURPLE)
+ vector_lab = TextMobject(r"$\hat{u}$").scale(0.8).move_to(np.array([1.2,-0.5,0])).set_color(GREEN_C)
+ domain_lab = TextMobject(r"$D$").scale(0.6).move_to(np.array([1,1,0])).set_color(GREEN_C)
+ func_lab = TextMobject(r"$z = f(x,y)$").scale(0.6).move_to(1*UP + 2.8*RIGHT).set_color(BLUE_C)
+ directional_deriv_lab = TextMobject(r"Slope = $D_{\hat{u}}f(x_0,y_0)$").scale(0.6).move_to(2.2*UP + 1.5*RIGHT).set_color(YELLOW_C)
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.set_camera_orientation(phi=65 * DEGREES, theta = 20*DEGREES)
+
+ self.play(ShowCreation(paraboloid))
+ self.add_fixed_in_frame_mobjects(func_lab)
+ self.wait()
+
+ #self.play(ShowCreation(circle))
+ self.bring_to_front(circle)
+ self.wait()
+ self.add_fixed_orientation_mobjects(domain_lab)
+ self.wait()
+
+ self.play(ShowCreation(plane), ShowCreation(parabola_curve))
+ self.play(ShowCreation(dot1), GrowArrow(line), ShowCreation(dot2))
+ self.add_fixed_orientation_mobjects(dot1_lab)
+ self.wait()
+ self.add_fixed_orientation_mobjects(dot2_lab)
+ self.wait()
+
+ self.play(ShowCreation(tangent_line))
+ self.add_fixed_in_frame_mobjects(directional_deriv_lab)
+ self.wait()
+
+ self.play(GrowArrow(vector))
+ self.add_fixed_orientation_mobjects(vector_lab)
+ self.wait()
+
+
+ self.begin_ambient_camera_rotation(rate=0.1)
+ self.wait(3)
+
+
diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/file2_gradient.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/file2_gradient.py new file mode 100644 index 0000000..e9fef50 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/file2_gradient.py @@ -0,0 +1,103 @@ +from manimlib.imports import *
+
+class Gradient(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes() # creates a 3D Axis
+
+
+ quadrant = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ 2*np.cos(u)
+ ]),u_min=0,u_max=PI/3,v_min=0,v_max=PI/2,checkerboard_colors=[GREEN_C, GREEN_E],
+ resolution=(15, 32)).scale(1)
+
+ quadrant_curve = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ 2*np.cos(u)
+ ]),u_min=34*DEGREES,u_max=38*DEGREES,v_min=0,v_max=PI/2,checkerboard_colors=[YELLOW_C, YELLOW_E],
+ resolution=(15, 32)).scale(1)
+
+
+
+ dot1 =Sphere(radius=0.05).move_to(np.array([1,1,0])).set_fill(YELLOW_C)
+ dot2 =Sphere(radius=0.05).move_to(np.array([1,1,1.732])).set_fill(YELLOW_C)
+
+ dot1_line = DashedLine(np.array([1,1,1.732]), np.array([0,2,2]), color = WHITE)
+ dot1_lab = TextMobject(r"$P_0(x_0,y_0,z_0)$").move_to(np.array([0,2.1,2.2])).set_color(YELLOW_C).scale(0.6)
+ #dot2_line = Line(np.array([0.8,0.8,0]), np.array([1,0.6,0]), color = PINK)
+
+ positive_vector = Arrow(np.array([1,1,0]), np.array([0.5,0.5,0]), buff=0.001, color = BLUE_C)
+ positive_gradient = Arrow(np.array([1,1,1.732]), np.array([0.5,0.5,1.9362]), buff=0.001, color = BLUE_C)
+ positive_gradient_lab = TextMobject(r"$\nabla f$").move_to(np.array([0.5,0.3,0])).set_color(BLUE_C).scale(0.5)
+
+ negative_vector = Arrow(np.array([1,1,0]), np.array([1.5,1.5,0]), buff=0.001, color = RED_C)
+ negative_gradient = Arrow(np.array([1,1,1.732]), np.array([1.5,1.5,1.322]), buff=0.001, color = RED_C)
+ negative_gradient_lab = TextMobject(r"$-\nabla f$").move_to(np.array([1.6,1.6,0])).set_color(RED_C).scale(0.5)
+
+ positive_vector_line = DashedLine(np.array([0.8,0.8,0]), np.array([1,-2,0]), color = WHITE)
+ positive_vector_lab = TextMobject(r"Most Rapid increase in $f$").move_to(np.array([1.6,-3.6,0])).set_color(BLUE_C).scale(0.6)
+ negative_vector_line = DashedLine(np.array([1.2,1.2,0]), np.array([3,-1.5,0]), color = WHITE)
+ negative_vector_lab = TextMobject(r"Most Rapid decrease in $f$").move_to(np.array([3.6,-3,0])).set_color(RED_C).scale(0.6)
+
+
+
+ line1 = DashedLine(np.array([0.5,0.5,0]), np.array([0.5,0.5,1.9362]), color = BLUE_C)
+ line2 = DashedLine(np.array([1,1,0]), np.array([1,1,1.732]), color = YELLOW_C)
+ line3 = DashedLine(np.array([1.5,1.5,0]), np.array([1.5,1.5,1.322]), color = RED_C)
+
+ curve_vector1 = Arrow(np.array([1,1,0]), np.array([1.5,0.5,0]), buff=0.001, color = YELLOW_C)
+ curve_vector2 = Arrow(np.array([1,1,0]), np.array([0.5,1.5,0]), buff=0.001, color = YELLOW_C)
+
+ curve_vector1_line = DashedLine(np.array([1.2,0.8,0]), np.array([1,2.5,0]), color = WHITE)
+ curve_vector2_line = DashedLine(np.array([0.8,1.2,0]), np.array([1,2.5,0]), color = WHITE)
+ curve_vector_lab = TextMobject(r"Zero Change in $f$").move_to(np.array([0.7,3.6,0])).set_color(PINK).scale(0.6)
+
+ #square = Square(side_length = 0.5).rotate(45*DEGREES).move_to(np.array([1.025,0.975,0]))
+ line_x = Line(np.array([0.8,0.8,0]), np.array([1,0.6,0]), color = PINK)
+ line_y = Line(np.array([1.2,0.8,0]), np.array([1,0.6,0]), color = PINK)
+
+ ninety_degree = VGroup(line_x, line_y)
+
+ self.set_camera_orientation(phi=60* DEGREES, theta = 20*DEGREES)
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(ShowCreation(quadrant))
+ self.wait()
+ self.play(ShowCreation(dot1), ShowCreation(dot2))
+ self.wait()
+ self.play(GrowArrow(positive_vector), GrowArrow(positive_gradient))
+ self.wait()
+ self.play(GrowArrow(negative_vector), GrowArrow(negative_gradient))
+ self.wait()
+ self.play(GrowArrow(line1), GrowArrow(line2), GrowArrow(line3))
+ self.wait()
+ self.play(ShowCreation(quadrant_curve))
+ self.wait()
+ self.play(GrowArrow(curve_vector1), GrowArrow(curve_vector2), ShowCreation(ninety_degree))
+ self.wait()
+ self.play(GrowArrow(dot1_line))
+ self.add_fixed_orientation_mobjects(dot1_lab)
+ self.wait()
+ self.play(GrowArrow(curve_vector1_line), GrowArrow(curve_vector2_line))
+ self.add_fixed_orientation_mobjects(curve_vector_lab)
+ self.wait()
+ self.add_fixed_orientation_mobjects(positive_gradient_lab, negative_gradient_lab)
+ self.wait()
+ self.play(GrowArrow(positive_vector_line), GrowArrow(negative_vector_line))
+ self.add_fixed_orientation_mobjects(positive_vector_lab, negative_vector_lab)
+ self.begin_ambient_camera_rotation(rate=0.1)
+ self.wait(3)
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/file3_gradient_level_curves.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/file3_gradient_level_curves.py new file mode 100644 index 0000000..a3b88e5 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/file3_gradient_level_curves.py @@ -0,0 +1,107 @@ +from manimlib.imports import *
+
+class GradientLevelCurves(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ paraboloid = ParametricSurface(
+ lambda u, v: np.array([
+ u*np.cos(v),
+ u*np.sin(v),
+ -u*u+2
+ ]),u_min=-1.414,u_max=1.414,v_min=0,v_max=2*PI, color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.1,
+ resolution=(15, 32)).scale(1)
+
+ plane_0 = Polygon(np.array([2,-2,0]),np.array([2,2,0]),np.array([-2,2,0]),np.array([-2,-2,0]),np.array([2,-2,0]), color = BLUE_E, fill_color = BLUE_E, fill_opacity = 0.3)
+ plane_0_lab = TextMobject("C = 0").move_to(0.4*UP+3.2*RIGHT).set_color(BLUE_E).scale(0.6)
+ circle_0 = Circle(radius = 1.414 , color = BLUE_E)
+ circle_0_lab = TextMobject("0").move_to(1.1*DOWN+1.1*RIGHT).set_color(BLUE_E).scale(0.6)
+
+ plane_0_5 = Polygon(np.array([2,-2,0.5]),np.array([2,2,0.5]),np.array([-2,2,0.5]),np.array([-2,-2,0.5]),np.array([2,-2,0.5]), color = GREEN_C, fill_color = GREEN_C, fill_opacity = 0.3)
+ plane_0_5_lab = TextMobject("C = 0.5").move_to(0.8*UP+3.4*RIGHT).set_color(GREEN_C).scale(0.6)
+ circle_0_5 = Circle(radius = 1.224 , color = GREEN_C)
+ circle_0_5_lab = TextMobject("0.5").move_to(0.9*DOWN+0.9*RIGHT).set_color(GREEN_C).scale(0.6)
+ circle_0_5_copy = circle_0_5.copy().move_to(np.array([0,0,0.5]))
+
+ plane_1 = Polygon(np.array([2,-2,1]),np.array([2,2,1]),np.array([-2,2,1]),np.array([-2,-2,1]),np.array([2,-2,1]), color = YELLOW_C, fill_color = YELLOW_C, fill_opacity = 0.3)
+ plane_1_lab = TextMobject("C = 1").move_to(1.2*UP+3.3*RIGHT).set_color(YELLOW_C).scale(0.6)
+ circle_1 = Circle(radius = 1 , color = YELLOW_C)
+ circle_1_lab = TextMobject("1").move_to(0.7*DOWN+0.7*RIGHT).set_color(YELLOW_C).scale(0.6)
+ circle_1_copy = circle_1.copy().move_to(np.array([0,0,1]))
+
+ plane_1_5 = Polygon(np.array([2,-2,1.5]),np.array([2,2,1.5]),np.array([-2,2,1.5]),np.array([-2,-2,1.5]),np.array([2,-2,1.5]), color = ORANGE, fill_color = ORANGE, fill_opacity = 0.3)
+ plane_1_5_lab = TextMobject("C = 1.5").move_to(1.7*UP+3.4*RIGHT).set_color(ORANGE).scale(0.6)
+ circle_1_5 = Circle(radius = 0.707 , color = ORANGE)
+ circle_1_5_lab = TextMobject("1.5").move_to(0.5*DOWN+0.5*RIGHT).set_color(ORANGE).scale(0.6)
+ circle_1_5_copy = circle_1_5.copy().move_to(np.array([0,0,1.5]))
+
+ plane_2 = Polygon(np.array([2,-2,2]),np.array([2,2,2]),np.array([-2,2,2]),np.array([-2,-2,2]),np.array([2,-2,2]), color = RED_C, fill_color = RED_C, fill_opacity = 0.3)
+ plane_2_lab = TextMobject("C = 2").move_to(2.1*UP+3.3*RIGHT).set_color(RED_C).scale(0.6)
+ dot_2 = Dot().set_fill(RED_C)
+ circle_2_lab = TextMobject("2").move_to(0.2*DOWN+0.2*RIGHT).set_color(RED_C).scale(0.6)
+ dot_2_copy = dot_2.copy().move_to(np.array([0,0,2]))
+
+ vector1 = Arrow(np.array([0.99,-0.99,0]), np.array([0.865,-0.865,0.5]), buff=0.01, color = RED_C).set_stroke(width=3)
+ gradient1 = Arrow(np.array([0.99,-0.99,0]), np.array([0.865,-0.865,0]), buff=0.01, color = RED_C).set_stroke(width=3)
+
+ vector2 = Arrow(np.array([0.865,-0.865,0.5]), np.array([0.707,-0.707,1]), buff=0.01, color = RED_C).set_stroke(width=3)
+ gradient2 = Arrow(np.array([0.865,-0.865,0]), np.array([0.707,-0.707,0]), buff=0.01, color = RED_C).set_stroke(width=3)
+
+ vector3 = Arrow(np.array([0.707,-0.707,1]), np.array([0.499,-0.499,1.5]), buff=0.01, color = RED_C).set_stroke(width=3)
+ gradient3 = Arrow(np.array([0.707,-0.707,0]), np.array([0.499,-0.499,0]), buff=0.01, color = RED_C).set_stroke(width=3)
+
+ vector4 = Arrow(np.array([0.499,-0.499,1.5]), np.array([0,0,2]), buff=0.01, color = RED_C).set_stroke(width=3)
+ gradient4 = Arrow(np.array([0.499,-0.499,0]), np.array([0,0,0]), buff=0.01, color = RED_C).set_stroke(width=3)
+
+
+ self.set_camera_orientation(phi=80 * DEGREES, theta = 0*DEGREES)
+ #self.set_camera_orientation(phi=45 * DEGREES, theta = -20*DEGREES)
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(Write(paraboloid))
+ self.wait()
+ self.play(ShowCreation(plane_0), ShowCreation(circle_0))
+ self.add_fixed_in_frame_mobjects(plane_0_lab)
+ self.wait()
+ self.play(ShowCreation(plane_0_5), ShowCreation(circle_0_5_copy), ShowCreation(circle_0_5))
+ self.add_fixed_in_frame_mobjects(plane_0_5_lab)
+ self.wait()
+ self.play(ShowCreation(plane_1), ShowCreation(circle_1_copy), ShowCreation(circle_1))
+ self.add_fixed_in_frame_mobjects(plane_1_lab)
+ self.wait()
+ self.play(ShowCreation(plane_1_5), ShowCreation(circle_1_5_copy), ShowCreation(circle_1_5))
+ self.add_fixed_in_frame_mobjects(plane_1_5_lab)
+ self.wait()
+ self.play(ShowCreation(plane_2), ShowCreation(dot_2_copy), ShowCreation(dot_2))
+ self.add_fixed_in_frame_mobjects(plane_2_lab)
+ self.wait()
+ self.move_camera(phi=60 * DEGREES, theta = 30*DEGREES,run_time=3)
+ self.play(FadeOut(plane_0), FadeOut(plane_0_lab), FadeOut(plane_0_5), FadeOut(plane_0_5_lab), FadeOut(plane_1), FadeOut(plane_1_lab), FadeOut(plane_1_5), FadeOut(plane_1_5_lab), FadeOut(plane_2), FadeOut(plane_2_lab))
+ self.play(FadeOut(circle_0_5_copy), FadeOut(circle_1_copy), FadeOut(circle_1_5_copy), FadeOut(dot_2_copy))
+
+ self.move_camera(phi=45 * DEGREES, theta = -20*DEGREES,run_time=3)
+ self.play(Write(vector1), Write(gradient1))
+ self.wait()
+ self.play(Write(vector2), Write(gradient2))
+ self.wait()
+ self.play(Write(vector3), Write(gradient3))
+ self.wait()
+ self.play(Write(vector4), Write(gradient4))
+ self.wait()
+ self.move_camera(phi=0 * DEGREES, theta = 0*DEGREES,run_time=3)
+ self.play(FadeOut(paraboloid))
+ self.play(FadeOut(vector1), FadeOut(vector2), FadeOut(vector3), FadeOut(vector4))
+ self.wait()
+ self.add_fixed_in_frame_mobjects(circle_0_lab, circle_0_5_lab, circle_1_lab, circle_1_5_lab,circle_2_lab)
+ self.wait(4)
+
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/gifs/file1_directional_deriv.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/gifs/file1_directional_deriv.gif Binary files differnew file mode 100644 index 0000000..39305d5 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/gifs/file1_directional_deriv.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/gifs/file2_gradient.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/gifs/file2_gradient.gif Binary files differnew file mode 100644 index 0000000..d96f330 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/gifs/file2_gradient.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/gifs/file3_gradient_level_curves.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/gifs/file3_gradient_level_curves.gif Binary files differnew file mode 100644 index 0000000..f1bf06a --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/directional-derivatives/gifs/file3_gradient_level_curves.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/Multivariable_Functions_Quiz.pdf b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/Multivariable_Functions_Quiz.pdf Binary files differindex 7895843..7895843 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/Multivariable_Functions_Quiz.pdf +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/Multivariable_Functions_Quiz.pdf diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/README.md b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/README.md new file mode 100644 index 0000000..0e6e8d3 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/README.md @@ -0,0 +1,17 @@ +**file1_multivar_func_examples** + + +**file2_multivariable_func_respresentation** + + +**file3_sphere** + + +**file4_vectorvf_sine** + + +**file5_vectorvf_helix** + + +**file6_derivative_vectorvf** + diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file1_multivar_func_examples.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file1_multivar_func_examples.py new file mode 100644 index 0000000..55b2b7e --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file1_multivar_func_examples.py @@ -0,0 +1,167 @@ +from manimlib.imports import *
+
+class Examples1(GraphScene):
+ def construct(self):
+
+ rectangle = Rectangle(height = 3, width = 4, color = GREEN)
+ rectangle_area_func = TexMobject("Area", "=", "f(", "Length", ",", "Breadth", ")").scale(0.6)
+ rectangle_area_func[0].set_color(RED_C)
+ rectangle_area_func[2].set_color(ORANGE)
+ rectangle_area_func[3].set_color(YELLOW_C)
+ rectangle_area_func[5].set_color(BLUE_C)
+ rectangle_area_func[6].set_color(ORANGE)
+
+
+ rectangle_area = TexMobject("Area", "=", "Length", "\\times", "Breadth").scale(0.6)
+ rectangle_area[0].set_color(RED_C)
+ rectangle_area[2].set_color(YELLOW_C)
+ rectangle_area[4].set_color(BLUE_C)
+
+
+ square = Square(side_length = 5, color = PURPLE)
+ square_area_func = TexMobject("Area", "=", "f(", "Length", ")")
+ square_area_func[0].set_color(GREEN_C)
+ square_area_func[2].set_color(ORANGE)
+ square_area_func[3].set_color(BLUE_C)
+ square_area_func[4].set_color(ORANGE)
+
+ square_area = TexMobject("Area", "=", "Length^2")
+ square_area[0].set_color(GREEN_C)
+ square_area[2].set_color(BLUE_C)
+
+
+ circle = Circle(radius = 2, color = PINK)
+ circle_area_func = TexMobject("Area", "=", "f(", "r", ")")
+ circle_area_func[0].set_color(YELLOW_C)
+ circle_area_func[2].set_color(ORANGE)
+ circle_area_func[3].set_color(GREEN_C)
+ circle_area_func[4].set_color(ORANGE)
+
+ circle_area = TexMobject("Area", "=", "\\pi", "r^2")
+ circle_area[0].set_color(YELLOW_C)
+ circle_area[2].set_color(BLUE_C)
+ circle_area[3].set_color(GREEN_C)
+
+ radius = Line(ORIGIN,2*RIGHT, color = RED_C)
+
+
+
+ braces_rect1 = Brace(rectangle, LEFT)
+ eq_text1 = braces_rect1.get_text("Length").set_color(YELLOW_C)
+ braces_rect2 = Brace(rectangle, UP)
+ eq_text2 = braces_rect2.get_text("Breadth").set_color(BLUE_C)
+
+ braces_square = Brace(square, LEFT)
+ braces_square_text = braces_square.get_text("Length").set_color(BLUE_C)
+
+ radius_text = TexMobject("r", color = GREEN_C).next_to(radius,UP)
+
+
+
+ self.play(ShowCreation(rectangle))
+ self.wait(1)
+ self.play(GrowFromCenter(braces_rect1),Write(eq_text1),GrowFromCenter(braces_rect2),Write(eq_text2))
+ self.wait(1)
+ self.play(Write(rectangle_area_func))
+ self.wait(1)
+ self.play(Transform(rectangle_area_func, rectangle_area))
+ self.wait(1)
+ self.play(FadeOut(braces_rect1),FadeOut(eq_text1),FadeOut(braces_rect2),FadeOut(eq_text2),FadeOut(rectangle_area_func))
+
+
+ self.play(Transform(rectangle, square))
+ self.wait(1)
+ self.play(GrowFromCenter(braces_square),Write(braces_square_text))
+ self.wait(1)
+ self.play(Write(square_area_func))
+ self.wait(1)
+ self.play(Transform(square_area_func, square_area))
+ self.wait(1)
+ self.play(FadeOut(braces_square),FadeOut(braces_square_text),FadeOut(square_area_func))
+
+
+ self.play(Transform(rectangle, circle))
+ self.wait(1)
+ self.play(ShowCreation(radius),Write(radius_text))
+ self.wait(1)
+ self.play(FadeOut(radius_text),FadeOut(radius))
+ self.wait(1)
+ self.play(Write(circle_area_func))
+ self.wait(1)
+ self.play(Transform(circle_area_func, circle_area))
+ self.wait(1)
+ self.play(FadeOut(circle_area_func))
+
+
+
+class Examples2(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ rectangle_x_y_0 = Polygon(np.array([-1,-2,0]),np.array([-1,2,0]),np.array([1,2,0]),np.array([1,-2,0]),np.array([-1,-2,0]), color = RED_E, fill_color = RED_C, fill_opacity = 0.1)
+ rectangle_x_y_3 = Polygon(np.array([-1,-2,3]),np.array([-1,2,3]),np.array([1,2,3]),np.array([1,-2,3]),np.array([-1,-2,3]), color = RED_E, fill_color = RED_C, fill_opacity = 0.1)
+
+ rectangle_y_z_1 = Polygon(np.array([1,-2,3]),np.array([1,2,3]),np.array([1,2,0]),np.array([1,-2,0]),np.array([1,-2,3]), color = RED_E, fill_color = RED_C, fill_opacity = 0.1)
+ rectangle_y_z_minus_1 = Polygon(np.array([-1,-2,3]),np.array([-1,2,3]),np.array([-1,2,0]),np.array([-1,-2,0]),np.array([-1,-2,3]), color = RED_E, fill_color = RED_C, fill_opacity = 0.1)
+
+ rectangle_x_z_2 = Polygon(np.array([1,2,3]),np.array([-1,2,3]),np.array([-1,2,0]),np.array([1,2,0]),np.array([1,2,3]), color = RED_E, fill_color = RED_C, fill_opacity = 0.1)
+ rectangle_x_z_minus_2 = Polygon(np.array([1,-2,3]),np.array([-1,-2,3]),np.array([-1,-2,0]),np.array([1,-2,0]),np.array([1,-2,3]), color = RED_E, fill_color = RED_C, fill_opacity = 0.1)
+
+ box = VGroup(rectangle_x_y_0, rectangle_x_y_3, rectangle_y_z_1, rectangle_y_z_minus_1, rectangle_x_z_2, rectangle_x_z_minus_2)
+
+ braces_rectangle_x_y_0 = Line(np.array([1,2,0]), np.array([1,-2,0]), color = BLUE_C)
+ braces_rectangle_x_y_0_text = TextMobject("Length").set_color(BLUE_C).move_to(np.array([2,-1,0]))
+
+ braces_rectangle_y_z_1 = Line(np.array([1,2,0]), np.array([1,2,3]), color = YELLOW_C)
+ braces_rectangle_y_z_1_text = TextMobject("Height").set_color(YELLOW_C).move_to(np.array([2,3.8,2]))
+
+ braces_rectangle_x_z_2 = Line(np.array([1,2,3]), np.array([-1,2,3]), color = PURPLE)
+ braces_rectangle_x_z_2_text = TextMobject("Breadth").set_color(PURPLE).move_to(np.array([0,3.8,3.3]))
+
+ box_area_func = TexMobject("Area =", "f(", "Length", ",", "Breadth", ",", "Height", ")").move_to(4*LEFT+3.5*UP).scale(0.6)
+ box_area_func[0].set_color(GREEN_C)
+ box_area_func[1].set_color(ORANGE)
+ box_area_func[2].set_color(BLUE_C)
+ box_area_func[4].set_color(PURPLE)
+ box_area_func[6].set_color(YELLOW_C)
+ box_area_func[7].set_color(ORANGE)
+
+ box_area_func_2 = TexMobject("Area =", "Length", "\\times", "Breadth", "\\times", "Height").move_to(4*LEFT+3.5*UP).scale(0.6)
+ box_area_func_2[0].set_color(GREEN_C)
+ box_area_func_2[1].set_color(BLUE_C)
+ box_area_func_2[3].set_color(PURPLE)
+ box_area_func_2[5].set_color(YELLOW_C)
+
+
+ self.set_camera_orientation(phi=70 * DEGREES, theta = 45*DEGREES)
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(3.7*UP)
+
+ self.add_fixed_in_frame_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(ShowCreation(box), ShowCreation(braces_rectangle_x_y_0))
+ self.add_fixed_orientation_mobjects(braces_rectangle_x_y_0_text)
+ self.play(ShowCreation(braces_rectangle_y_z_1))
+ self.add_fixed_orientation_mobjects(braces_rectangle_y_z_1_text)
+ self.play(ShowCreation(braces_rectangle_x_z_2))
+ self.add_fixed_orientation_mobjects(braces_rectangle_x_z_2_text)
+ self.wait(2)
+
+ self.move_camera(phi=60* DEGREES,theta=80*DEGREES)
+ self.add_fixed_in_frame_mobjects(box_area_func)
+ self.play(Write(box_area_func))
+ self.wait()
+
+
+ self.play(ReplacementTransform(box_area_func,box_area_func_2))
+ self.add_fixed_in_frame_mobjects(box_area_func_2)
+
+
+ self.wait(3)
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file2_multivariable_func_respresentation.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file2_multivariable_func_respresentation.py new file mode 100644 index 0000000..d10ff0a --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file2_multivariable_func_respresentation.py @@ -0,0 +1,98 @@ +from manimlib.imports import *
+
+class MultivariableFunc(Scene):
+ def construct(self):
+
+ topic = TextMobject("Multivariable Functions")
+ topic.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+ topic.scale(1.5)
+
+ self.play(Write(topic))
+ self.wait()
+ self.play(FadeOut(topic))
+
+
+ #circle = Circle()
+ #circle.scale(3)
+
+ scalar_function = TextMobject("Scalar Valued Function")
+ scalar_function.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+ scalar_function.scale(1.5)
+ scalar_function.move_to(2.5*UP)
+
+ rectangle = Rectangle(height = 2, width = 4)
+ rectangle.set_color(PURPLE)
+
+ eqn1 = TextMobject(r"f(x,y) = $x^2y$")
+ eqn1.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE)
+
+
+
+ number1 = TextMobject("(2,1)")
+ number1.move_to(2.5*UP+ 4*LEFT)
+ number1.scale(1.2)
+ number1.set_color(ORANGE)
+
+ output1 = TextMobject("4")
+ output1.scale(1.5)
+ output1.set_color(BLUE_C)
+ output1.move_to(3*RIGHT)
+
+ eqn1_1 = TextMobject(r"f(2,1) = $2^2(1)$")
+ eqn1_1.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE)
+
+
+ self.play(Write(eqn1),ShowCreation(rectangle))
+ self.wait()
+ self.play(ApplyMethod(number1.move_to, 3*LEFT))
+ self.play(FadeOut(number1))
+ self.play(Transform(eqn1, eqn1_1))
+ self.wait()
+ self.play(ApplyMethod(output1.move_to, 2.5*DOWN+4*RIGHT))
+ self.wait()
+ self.play(Write(scalar_function))
+ self.play(FadeOut(output1), FadeOut(scalar_function), FadeOut(eqn1))
+
+
+ vector_function = TextMobject("Vector Valued Function")
+ vector_function.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+ vector_function.scale(1.5)
+ vector_function.move_to(2.5*UP)
+
+
+ eqn2 = TextMobject(r"f(x,y,z) = $ \begin{bmatrix} x^2y \\ 2yz \end{bmatrix}$")
+ eqn2.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+
+ number2 = TextMobject("(2,1,3)")
+ number2.move_to(2.5*UP+ 4*LEFT)
+ number2.scale(1.2)
+ number2.set_color(ORANGE)
+
+ output2 = TextMobject(r"$ \begin{bmatrix} 4 \\ 6 \end{bmatrix}$")
+ #output2.scale(1.5)
+ output2.set_color(BLUE_C)
+ output2.move_to(3*RIGHT)
+
+ #eqn2_1 = TextMobject(r"f(2,1,3) = $2^2(1) + 2(1)(3)$")
+ #eqn2_1.set_color(YELLOW)
+
+ #eqn2_2 = TextMobject(r"f(2,1,3) = $2 + 6$")
+ #eqn2_2.set_color(YELLOW)
+
+
+ self.play(Write(eqn2))
+
+ self.wait()
+ self.play(ApplyMethod(number2.move_to, 3*LEFT))
+ self.play(FadeOut(number2))
+
+ #self.play(Transform(eqn2, eqn2_1))
+ #self.wait(1)
+ #self.play(Transform(eqn2, eqn2_2))
+ #self.wait(1)
+
+ self.play(ApplyMethod(output2.move_to, 2.5*DOWN+4*RIGHT))
+ self.wait()
+ self.play(Write(vector_function))
+ self.play(FadeOut(output2),FadeOut(eqn2), FadeOut(vector_function), FadeOut(rectangle))
+ self.wait()
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file3_sphere.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file3_sphere.py new file mode 100644 index 0000000..86239ae --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file3_sphere.py @@ -0,0 +1,177 @@ +from manimlib.imports import *
+
+class Sphere(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes() # creates a 3D Axis
+
+ text3d = TextMobject(r"$f(x,y) \rightarrow Point(x,y,z)$")
+ text3d1 = TextMobject(r"$f(x,y) \rightarrow Point(x,y, \sqrt{r^2 - x^2 - y^2})$")
+ self.add_fixed_in_frame_mobjects(text3d)
+ text3d.scale(0.7)
+ text3d1.scale(0.7)
+ text3d.to_corner(UL)
+ text3d1.to_corner(UL)
+ text3d.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+ text3d1.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+ self.play(Write(text3d))
+ self.wait(1)
+
+ self.play(Transform(text3d,text3d1))
+ self.add_fixed_in_frame_mobjects(text3d1)
+ self.play(FadeOut(text3d))
+
+ sphere = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ 2*np.cos(u)
+ ]),u_min=0,u_max=PI,v_min=0,v_max=2*PI,checkerboard_colors=[RED_D, RED_E],
+ resolution=(15, 32)).scale(1)
+
+
+ #Experiment with circles by changing difference value of u and v
+ '''
+ sphere_points = [np.array([2*np.sin(u*DEGREES)*np.cos(v*DEGREES), 2*np.sin(u*DEGREES)*np.sin(v*DEGREES), 2*np.cos(u*DEGREES)]) for u in range(0, 185, 5) for v in range(0, 365, 5)]
+
+ sphere_spheres = [Dot().move_to(pts) for pts in sphere_points]
+
+ sphere = VGroup(*sphere_spheres)
+ '''
+
+ self.set_camera_orientation(phi=75 * DEGREES, theta = 45*DEGREES)
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ dot_x_y1 = Dot().scale(0.75).set_fill(RED_C).move_to(np.array([-1,1,0]))
+ dot_x_y_z1 = Dot().scale(0.75).set_fill(RED_C).move_to(np.array([-1,1,1.414]))
+ dot_x_y_z_1 = Dot().scale(0.75).set_fill(RED_C).move_to(np.array([-1,1,-1.414]))
+ line1 = DashedLine(np.array([-1,1,-1.414]), np.array([-1,1,1.414]), color = YELLOW_C)
+
+ point_x_y1 = TexMobject("(-1,1,0)").set_color(BLUE_C).move_to(np.array([-1.5,1.5,0])).scale(0.5)
+ point_x_y_z1 = TexMobject("(-1,1,\\sqrt{r^2 - x^2 - y^2})").set_color(BLUE_C).move_to(np.array([-1.5,1.5,1.414])).scale(0.5)
+ point_x_y_z1_2 = TexMobject("(-1,1,\\sqrt{4 - x^2 - y^2})").set_color(BLUE_C).move_to(np.array([-1.5,1.5,1.414])).scale(0.5)
+ point_x_y_z1_3 = TexMobject("(-1,1,\\sqrt{4 - 1 - 1})").set_color(BLUE_C).move_to(np.array([-1.5,1.5,1.414])).scale(0.5)
+ point_x_y_z1_4 = TexMobject("(-1,1,\\sqrt{2})").set_color(BLUE_C).move_to(np.array([-1.5,1.5,1.414])).scale(0.5)
+ point_x_y_z1_5 = TexMobject("(-1,1,1.414)").set_color(BLUE_C).move_to(np.array([-1.5,1.5,1.414])).scale(0.5)
+
+ point_x_y_z_1 = TexMobject("(-1,1,\\sqrt{r^2 - x^2 - y^2})").set_color(BLUE_C).move_to(np.array([-1.5,1.5,-1.414])).scale(0.5)
+ point_x_y_z_1_2 = TexMobject("(-1,1,\\sqrt{4 - x^2 - y^2})").set_color(BLUE_C).move_to(np.array([-1.5,1.5,-1.414])).scale(0.5)
+ point_x_y_z_1_3 = TexMobject("(-1,1,\\sqrt{4 - 1 - 1})").set_color(BLUE_C).move_to(np.array([-1.5,1.5,-1.414])).scale(0.5)
+ point_x_y_z_1_4 = TexMobject("(-1,1,\\sqrt{2})").set_color(BLUE_C).move_to(np.array([-1.5,1.5,-1.414])).scale(0.5)
+ point_x_y_z_1_5 = TexMobject("(-1,1,-1.414)").set_color(BLUE_C).move_to(np.array([-1.5,1.5,-1.414])).scale(0.5)
+
+
+ self.play(ShowCreation(dot_x_y1))
+ self.add_fixed_orientation_mobjects(point_x_y1)
+ self.play(ShowCreation(dot_x_y_z1), ShowCreation(dot_x_y_z_1), ShowCreation(line1))
+ self.add_fixed_orientation_mobjects(point_x_y_z1, point_x_y_z_1)
+ self.wait(0.5)
+ self.play(ReplacementTransform(point_x_y_z1,point_x_y_z1_2), ReplacementTransform(point_x_y_z_1,point_x_y_z_1_2))
+ self.add_fixed_orientation_mobjects(point_x_y_z1_2, point_x_y_z_1_2)
+
+ self.wait(0.5)
+ self.play(ReplacementTransform(point_x_y_z1_2,point_x_y_z1_3), ReplacementTransform(point_x_y_z_1_2,point_x_y_z_1_3))
+ self.add_fixed_orientation_mobjects(point_x_y_z1_3, point_x_y_z_1_3)
+ self.wait(0.5)
+ self.play(ReplacementTransform(point_x_y_z1_3,point_x_y_z1_4), ReplacementTransform(point_x_y_z_1_3,point_x_y_z_1_4))
+ self.add_fixed_orientation_mobjects(point_x_y_z1_4, point_x_y_z_1_4)
+ self.wait(0.5)
+ self.play(ReplacementTransform(point_x_y_z1_4,point_x_y_z1_5), ReplacementTransform(point_x_y_z_1_4,point_x_y_z_1_5))
+ self.add_fixed_orientation_mobjects(point_x_y_z1_5, point_x_y_z_1_5)
+
+
+
+ dot_x_y2 = Dot().scale(0.75).set_fill(RED_C).move_to(np.array([0.5,-0.5,0]))
+ dot_x_y_z2 = Dot().scale(0.75).set_fill(RED_C).move_to(np.array([0.5,-0.5,1.87]))
+ dot_x_y_z_2 = Dot().scale(0.75).set_fill(RED_C).move_to(np.array([0.5,-0.5,-1.87]))
+ line2 = DashedLine(np.array([0.5,-0.5,-1.87]), np.array([0.5,-0.5,1.87]), color = YELLOW_C)
+
+ point_x_y2 = TexMobject("(0.5,-0.5,0)").set_color(BLUE_C).move_to(np.array([1.5,-1.5,0])).scale(0.5)
+ point_x_y_z2 = TexMobject("(0.5,-0.5,\\sqrt{r^2 - x^2 - y^2})").set_color(BLUE_C).move_to(np.array([1.5,-1.5,1.87])).scale(0.5)
+ point_x_y_z2_2 = TexMobject("(0.5,-0.5,\\sqrt{4 - x^2 - y^2})").set_color(BLUE_C).move_to(np.array([1.5,-1.5,1.87])).scale(0.5)
+ point_x_y_z2_3 = TexMobject("(0.5,-0.5,\\sqrt{4 - 0.25 - 0.25})").set_color(BLUE_C).move_to(np.array([1.5,-1.5,1.87])).scale(0.5)
+ point_x_y_z2_4 = TexMobject("(0.5,-0.5,\\sqrt{3.5})").set_color(BLUE_C).move_to(np.array([1.5,-1.5,1.87])).scale(0.5)
+ point_x_y_z2_5 = TexMobject("(0.5,-0.5,1.87)").set_color(BLUE_C).move_to(np.array([1.5,-1.5,1.87])).scale(0.5)
+
+ point_x_y_z_2 = TexMobject("(0.5,-0.5,\\sqrt{r^2 - x^2 - y^2})").set_color(BLUE_C).move_to(np.array([1.5,-1.5,-1.87])).scale(0.5)
+ point_x_y_z_2_2 = TexMobject("(0.5,-0.5,\\sqrt{4 - x^2 - y^2})").set_color(BLUE_C).move_to(np.array([1.5,-1.5,-1.87])).scale(0.5)
+ point_x_y_z_2_3 = TexMobject("(0.5,-0.5,\\sqrt{4 - 0.25 - 0.25})").set_color(BLUE_C).move_to(np.array([1.5,-1.5,-1.87])).scale(0.5)
+ point_x_y_z_2_4 = TexMobject("(0.5,-0.5,\\sqrt{3.5})").set_color(BLUE_C).move_to(np.array([1.5,-1.5,-1.87])).scale(0.5)
+ point_x_y_z_2_5 = TexMobject("(0.5,-0.5,-1.87)").set_color(BLUE_C).move_to(np.array([1.5,-1.5,-1.87])).scale(0.5)
+
+
+ self.play(ShowCreation(dot_x_y2))
+ self.add_fixed_orientation_mobjects(point_x_y2)
+ self.play(ShowCreation(dot_x_y_z2), ShowCreation(dot_x_y_z_2), ShowCreation(line2))
+ self.add_fixed_orientation_mobjects(point_x_y_z2, point_x_y_z_2)
+ self.wait(0.5)
+ self.play(ReplacementTransform(point_x_y_z2,point_x_y_z2_2), ReplacementTransform(point_x_y_z_2,point_x_y_z_2_2))
+ self.add_fixed_orientation_mobjects(point_x_y_z2_2, point_x_y_z_2_2)
+
+ self.wait(0.5)
+ self.play(ReplacementTransform(point_x_y_z2_2,point_x_y_z2_3), ReplacementTransform(point_x_y_z_2_2,point_x_y_z_2_3))
+ self.add_fixed_orientation_mobjects(point_x_y_z2_3, point_x_y_z_2_3)
+ self.wait(0.5)
+ self.play(ReplacementTransform(point_x_y_z2_3,point_x_y_z2_4), ReplacementTransform(point_x_y_z_2_3,point_x_y_z_2_4))
+ self.add_fixed_orientation_mobjects(point_x_y_z2_4, point_x_y_z_2_4)
+ self.wait(0.5)
+ self.play(ReplacementTransform(point_x_y_z2_4,point_x_y_z2_5), ReplacementTransform(point_x_y_z_2_4,point_x_y_z_2_5))
+ self.add_fixed_orientation_mobjects(point_x_y_z2_5, point_x_y_z_2_5)
+
+ self.play(FadeOut(point_x_y1), FadeOut(point_x_y_z1_5), FadeOut(point_x_y_z_1_5), FadeOut(dot_x_y1), FadeOut(dot_x_y_z1), FadeOut(dot_x_y_z_1), FadeOut(line1))
+ self.play(FadeOut(point_x_y2), FadeOut(point_x_y_z2_5), FadeOut(point_x_y_z_2_5), FadeOut(dot_x_y2), FadeOut(dot_x_y_z2), FadeOut(dot_x_y_z_2), FadeOut(line2))
+
+
+
+
+ sphere_final = []
+
+ for u in range(0, 180, 15):
+ sphere_points1 = [np.array([2*np.sin(u*DEGREES)*np.cos(v*DEGREES), 2*np.sin(u*DEGREES)*np.sin(v*DEGREES), 2*np.cos(u*DEGREES)]) for v in range(0, 370, 10)]
+ sphere_dots1 = [Dot().scale(0.75).set_fill(RED_C).move_to(pts) for pts in sphere_points1]
+
+ sphere_points2 = [np.array([2*np.sin((u+5)*DEGREES)*np.cos(v*DEGREES), 2*np.sin((u+5)*DEGREES)*np.sin(v*DEGREES), 2*np.cos((u+5)*DEGREES)]) for v in range(0, 370, 10)]
+ sphere_dots2 = [Dot().scale(0.75).set_fill(RED_C).move_to(pts) for pts in sphere_points2]
+
+ sphere_points3 = [np.array([2*np.sin((u+10)*DEGREES)*np.cos(v*DEGREES), 2*np.sin((u+10)*DEGREES)*np.sin(v*DEGREES), 2*np.cos((u+10)*DEGREES)]) for v in range(0, 370, 10)]
+ sphere_dots3 = [Dot().scale(0.75).set_fill(RED_C).move_to(pts) for pts in sphere_points3]
+
+ sphere_final = sphere_final + sphere_dots1 + sphere_dots2 + sphere_dots3
+
+ sphere_dots = sphere_dots1 + sphere_dots2 + sphere_dots3
+
+ sphere_with_dots = VGroup(*sphere_dots)
+ self.play(ShowCreation(sphere_with_dots))
+
+ sphere_final_with_dots = VGroup(*sphere_final)
+
+
+ self.begin_ambient_camera_rotation(rate=0.5)
+ self.wait(3)
+ self.play(ReplacementTransform(sphere_final_with_dots, sphere))
+ self.wait(5)
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_vectorvf_sine.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file4_vectorvf_sine.py index 06e225e..06e225e 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_vectorvf_sine.py +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file4_vectorvf_sine.py diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file5_vectorvf_helix.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file5_vectorvf_helix.py new file mode 100644 index 0000000..fc151ac --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file5_vectorvf_helix.py @@ -0,0 +1,92 @@ +from manimlib.imports import *
+
+class Helix(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes() # creates a 3D Axis
+
+ helix1=ParametricFunction(
+ lambda u : np.array([
+ 1.5*np.cos(u),
+ 1.5*np.sin(u),
+ u/4
+ ]),color=PURPLE,t_min=-TAU,t_max=TAU,
+ )
+
+ helix2=ParametricFunction(
+ lambda u : np.array([
+ 2*np.cos(u),
+ 2*np.sin(u),
+ u/2
+ ]),color=GREEN_C,t_min=-TAU,t_max=TAU,
+ )
+
+ function = TexMobject("f(", "r", ",", "\\theta", ")", "=", "[", "r", "\\cos", "\\theta", ",", "r", "\\sin" ,"\\theta", ",", "h" ,"\\theta", "]" ).scale(0.6).to_corner(UL)
+ function.set_color_by_tex(r"\theta", BLUE_C)
+ function.set_color_by_tex(r"r", RED_C)
+ function.set_color_by_tex(r"\cos", GREEN_C)
+ function.set_color_by_tex(r"\sin", YELLOW_C)
+ function[0].set_color(ORANGE)
+ function[4].set_color(ORANGE)
+
+
+ self.add_fixed_in_frame_mobjects(function)
+
+ self.set_camera_orientation(phi=60*DEGREES, theta = 45*DEGREES)
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+
+ dot1 = Dot().rotate(PI/2).set_color(RED_C)
+ alpha1 = ValueTracker(0)
+ vector1 = self.get_vector(alpha1.get_value(),helix1)
+ dot1.add_updater(lambda m: m.move_to(vector1.get_end()))
+ self.play(
+ ShowCreation(helix1),
+ GrowFromCenter(dot1),
+ GrowArrow(vector1)
+ )
+ vector1.add_updater(
+ lambda m: m.become(
+ self.get_vector(alpha1.get_value()%1,helix1)
+ )
+ )
+ self.add(vector1,dot1)
+ self.play(alpha1.increment_value, 1, run_time=10, rate_func=linear)
+
+
+ self.play(FadeOut(vector1), FadeOut(dot1))
+ self.play(ReplacementTransform(helix1, helix2))
+
+
+ dot2 = Dot().rotate(PI/2).set_color(RED_C)
+ alpha2 = ValueTracker(0)
+ vector2 = self.get_vector(alpha2.get_value(),helix2)
+ dot2.add_updater(lambda m: m.move_to(vector2.get_end()))
+ self.play(
+ ShowCreation(helix2),
+ GrowFromCenter(dot2),
+ GrowArrow(vector2)
+ )
+ vector2.add_updater(
+ lambda m: m.become(
+ self.get_vector(alpha2.get_value()%1,helix2)
+ )
+ )
+ self.add(vector2,dot2)
+ self.play(alpha2.increment_value, 1, run_time=10, rate_func=linear)
+ self.wait()
+
+
+
+ def get_vector(self, proportion, curve):
+ vector = Line(np.array([0,0,0]), curve.point_from_proportion(proportion), color = YELLOW_C, buff=0)
+ return vector
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_derivative_vectorvf.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file6_derivative_vectorvf.py index 466e389..466e389 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Multivariable Functions/multivariable_func_derivative_vectorvf.py +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/file6_derivative_vectorvf.py diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file1_multivar_func_examples.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file1_multivar_func_examples.gif Binary files differnew file mode 100644 index 0000000..43c3a42 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file1_multivar_func_examples.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file2_multivariable_func_respresentation.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file2_multivariable_func_respresentation.gif Binary files differnew file mode 100644 index 0000000..8c4506c --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file2_multivariable_func_respresentation.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file3_sphere.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file3_sphere.gif Binary files differnew file mode 100644 index 0000000..3e35ec8 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file3_sphere.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file4_vectorvf_sine.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file4_vectorvf_sine.gif Binary files differnew file mode 100644 index 0000000..215459e --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file4_vectorvf_sine.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file5_vectorvf_helix.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file5_vectorvf_helix.gif Binary files differnew file mode 100644 index 0000000..c3d37f6 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file5_vectorvf_helix.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file6_derivative_vectorvf.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file6_derivative_vectorvf.gif Binary files differnew file mode 100644 index 0000000..9ea94e4 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-functions/gifs/file6_derivative_vectorvf.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/Limits_and_Continuity_of_Multivariable_Function_Quiz.pdf b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/Limits_and_Continuity_of_Multivariable_Function_Quiz.pdf Binary files differnew file mode 100644 index 0000000..99918e5 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/Limits_and_Continuity_of_Multivariable_Function_Quiz.pdf diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/README.md b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/README.md new file mode 100644 index 0000000..c01ddc5 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/README.md @@ -0,0 +1,14 @@ +**file1_epsilon_delta_defn** + + +**file2_limit_approach_point** + + +**file3_limit_approach_point_3d** + + +**file4_limit_different_point** + + +**file5_continuity_func** + diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file1_epsilon_delta_defn.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file1_epsilon_delta_defn.py new file mode 100644 index 0000000..803c122 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file1_epsilon_delta_defn.py @@ -0,0 +1,179 @@ +from manimlib.imports import *
+
+class EpsilonDelta(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes() # creates a 3D Axis
+
+
+ sphere = ParametricSurface(
+ lambda u, v: np.array([
+ 3*np.sin(u)*np.cos(v),
+ 3*np.sin(u)*np.sin(v),
+ 3*np.cos(u)
+ ]),u_min=0,u_max=PI/4,v_min=PI/2,v_max=PI,checkerboard_colors=[RED_D, RED_E],
+ resolution=(15, 32)).scale(1)
+
+
+ cylinder_z = ParametricSurface(
+ lambda u, v: np.array([
+ 0.25*np.cos(TAU * v),
+ 1.8* (1 - u),
+ 0.25*np.sin(TAU * v)
+
+ ]),
+ checkerboard_colors=[YELLOW_C, YELLOW_E], resolution=(6, 32)).fade(0.2).rotate(PI/4).move_to(np.array([-0.65,0.65,2.54]))
+
+
+ cylinder_x = ParametricSurface(
+ lambda u, v: np.array([
+ 0.3*np.cos(TAU * v)-1,
+ 0.3*np.sin(TAU * v)+1,
+ 2.6*(1 - u)
+ ]),
+ checkerboard_colors=[BLUE_C, BLUE_E], resolution=(6, 32)).fade(0.2)
+
+
+ delta_circle = Circle(radius= 0.3, color = BLACK).shift(1*LEFT+1*UP).set_fill(GREEN_E, opacity = 0.5)
+
+ epsilon_circle = [np.array([0.25*np.cos(i*DEGREES),0,0.25*np.sin(i*DEGREES)]) for i in range(361)]
+
+ epsilon_circle_polygon = Polygon(*epsilon_circle, color = RED_E, fill_color = RED_E, fill_opacity = 0.5).rotate(PI/4).move_to(np.array([0,0,2.54]))
+
+
+ dot_circle = Dot().move_to(np.array([-1,1,0])).set_fill("#000080")
+
+ dot_surface = Dot().rotate(-PI/4).scale(1.5).move_to(np.array([-1.2,1.2,2.7])).set_fill("#000080")
+
+ dot_L_epsilon1 = Polygon(*[np.array([0.05*np.cos(i*DEGREES),0,0.05*np.sin(i*DEGREES)]) for i in range(361)], color = "#000080", fill_color = "#000080", fill_opacity = 1).rotate(PI/4).move_to(np.array([0,0,2.3]))
+
+ dot_L_epsilon2 = Polygon(*[np.array([0.05*np.cos(i*DEGREES),0,0.05*np.sin(i*DEGREES)]) for i in range(361)], color = "#000080", fill_color = "#000080", fill_opacity = 1).rotate(PI/4).move_to(np.array([0,0,2.8]))
+
+ dot_L = Polygon(*[np.array([0.05*np.cos(i*DEGREES),0,0.05*np.sin(i*DEGREES)]) for i in range(361)], color = "#006400", fill_color = "#006400", fill_opacity = 1).rotate(PI/4).move_to(np.array([0,0,2.54]))
+
+
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.set_camera_orientation(phi=75*DEGREES,theta=135*DEGREES)
+ #self.set_camera_orientation(phi=80*DEGREES,theta=45*DEGREES)
+
+
+ self.play(ShowCreation(sphere),ShowCreation(delta_circle), ShowCreation(dot_circle))
+
+ temp_circle_center = TextMobject(r"$(a,b,0)$").scale(0.6).set_color(BLUE_C).move_to(1.7*LEFT+1.1*UP)
+ self.add_fixed_orientation_mobjects(temp_circle_center)
+ self.wait()
+
+ delta_lab = TextMobject(r"$\delta$", r"$-$", "disk").scale(0.5).move_to(0.6*LEFT+1.7*UP)
+ delta_lab[0].set_color(PINK).scale(1.3)
+ delta_lab[1].set_color(ORANGE)
+ delta_lab[2].set_color(GREEN_E)
+
+ self.add_fixed_orientation_mobjects(delta_lab)
+
+ self.play(ShowCreation(dot_surface))
+
+ temp_curve_circle_center = TextMobject(r"$(a,b,L)$").scale(0.6).set_color("#006400").move_to(np.array([-2,1,2.7]))
+ self.add_fixed_orientation_mobjects(temp_curve_circle_center)
+
+
+ self.wait()
+ self.play(ShowCreation(cylinder_x), FadeOut(dot_surface))
+ self.wait()
+
+ self.move_camera(phi=0* DEGREES,theta=135*DEGREES)
+ self.wait()
+
+ self.move_camera(phi=80* DEGREES,theta=225*DEGREES)
+ self.wait()
+
+ self.play(FadeOut(delta_lab), ShowCreation(cylinder_z))
+ self.wait()
+
+ self.play(FadeOut(temp_circle_center), FadeOut(temp_curve_circle_center),ShowCreation(epsilon_circle_polygon))
+
+ self.move_camera(phi=80* DEGREES,theta=325*DEGREES)
+
+ dot_L_epsilon1_lab = TextMobject(r"$L$", r"$-$", r"$\epsilon$").scale(0.6).move_to(np.array([-0.4,-0.4,2.3]))
+ dot_L_epsilon1_lab[0].set_color("#D4108A")
+ dot_L_epsilon1_lab[1].set_color("#006400")
+ dot_L_epsilon1_lab[2].set_color("#4DC8A1").scale(1.5)
+
+ dot_L_epsilon2_lab = TextMobject(r"$L$", r"$+$", r"$\epsilon$").scale(0.6).move_to(np.array([-0.4,-0.4,2.8]))
+ dot_L_epsilon2_lab[0].set_color("#D4108A")
+ dot_L_epsilon2_lab[1].set_color("#006400")
+ dot_L_epsilon2_lab[2].set_color("#4DC8A1").scale(1.5)
+
+ dot_L_lab = TextMobject(r"$L$").scale(0.6).set_color("#D4108A").move_to(np.array([-0.4,-0.4,2.54]))
+
+
+ self.play(ShowCreation(dot_L_epsilon1), ShowCreation(dot_L), ShowCreation(dot_L_epsilon2))
+ self.add_fixed_orientation_mobjects(dot_L_epsilon1_lab, dot_L_epsilon2_lab, dot_L_lab)
+ self.wait(4)
+
+ self.move_camera(phi=80* DEGREES,theta=45*DEGREES)
+ self.wait(2)
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+ '''
+
+
+
+
+
+
+
+
+
+
+
+ delta_lab = TextMobject(r"$\delta - disk$")
+ delta_lab.scale(0.5)
+ delta_lab.set_color(PINK)
+
+ self.play(ShowCreation(circle_center))
+ self.add_fixed_in_frame_mobjects(temp_circle_center)
+ temp_circle_center.move_to(1.5*RIGHT)
+ self.play(Write(temp_circle_center))
+
+ self.play(ShowCreation(curve_circle_center))
+ self.add_fixed_in_frame_mobjects(temp_curve_circle_center)
+ temp_curve_circle_center.move_to(1.9*UP+1*RIGHT)
+ self.play(Write(temp_curve_circle_center))
+
+
+ self.add_fixed_in_frame_mobjects(delta_lab)
+ delta_lab.move_to(0.4*DOWN+1.7*RIGHT)
+ self.play(Write(delta_lab))
+
+
+
+
+
+ self.begin_ambient_camera_rotation(rate=0.2)
+
+ self.play(ShowCreation(circle), ShowCreation(line1), ShowCreation(line2))
+ self.play(ShowCreation(line3), ShowCreation(line4))
+ self.wait(8)
+ '''
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Limits and Continuity of Multivariable Functions/limit_approach_point.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file2_limit_approach_point.py index 57d1d45..57d1d45 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Limits and Continuity of Multivariable Functions/limit_approach_point.py +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file2_limit_approach_point.py diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file3_limit_approach_point_3d.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file3_limit_approach_point_3d.py new file mode 100644 index 0000000..f1007a4 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file3_limit_approach_point_3d.py @@ -0,0 +1,152 @@ +from manimlib.imports import *
+
+class Limit(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ text3d = TextMobject(r"$f(x,y) = \frac{x - y}{x - 1}$")
+ self.add_fixed_in_frame_mobjects(text3d)
+
+ text3d.to_corner(UL)
+
+ text3d.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+
+ self.play(Write(text3d))
+ self.wait(1)
+
+ limit_func = ParametricSurface(
+ lambda u, v: np.array([
+ 3*np.sin(u)*np.cos(v),
+ 3*np.sin(u)*np.sin(v),
+ (3*np.sin(u)*np.cos(v) - 3*np.sin(u)*np.sin(v))/2*(3*np.sin(u)*np.cos(v) - 1)
+ ]),u_min=0,u_max=PI,v_min=0,v_max=2*PI, color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.1,
+ resolution=(15, 32)).scale(1)
+
+ limit_y_x =ParametricFunction(
+ lambda u : np.array([
+ u,
+ u,
+ 0
+ ]),color=GREEN_D,t_min=-3,t_max=3,
+ )
+
+ limit_y_1 =ParametricFunction(
+ lambda u : np.array([
+ u,
+ 1,
+ 1/2
+ ]),color=BLUE_D,t_min=-3,t_max=3,
+ )
+
+ limit_y_x_2 =ParametricFunction(
+ lambda u : np.array([
+ u,
+ u*u,
+ (u - u*u)/2*(u - 1)
+ ]),color=RED_D,t_min=-3,t_max=3,
+ )
+
+ limit_y_2_x =ParametricFunction(
+ lambda u : np.array([
+ u,
+ 2 - u,
+ 1
+ ]),color=YELLOW_D,t_min=-3,t_max=3,
+ )
+
+ plane_y_x = Polygon(np.array([-3,-3,-3]),np.array([3,3,-3]),np.array([3,3,3]),np.array([-3,-3,3]),np.array([-3,-3,-3]), color = GREEN_C, fill_color = GREEN_C, fill_opacity = 0.1)
+ plane_y_x_text = TextMobject(r"$y = x$", color = GREEN_C).move_to(np.array([5,0,3]))
+
+ plane_y_1 = Polygon(np.array([-3,1,-3]),np.array([3,1,-3]),np.array([3,1,3]),np.array([-3,1,3]),np.array([-3,1,-3]), color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.1)
+ plane_y_1_text = TextMobject(r"$y = 1$", color = BLUE_C).move_to(np.array([5,0,2.5]))
+
+
+ #Creating plane y = x^2
+ ######
+ y_x_2 = []
+ y_x_2.append(np.array([2, 4, -3]))
+ y_x_2.append(np.array([2, 4, 3]))
+ y_x_2_1 = [np.array([i, i*i, 3]) for i in np.arange(1.9,-2.1, -0.1)]
+
+ y_x_2 = y_x_2 + y_x_2_1
+
+ y_x_2.append(np.array([-2, 4, 3]))
+ y_x_2.append(np.array([-2, 4, -3]))
+
+ y_x_2_2 = [np.array([i, i*i, -3]) for i in np.arange(-2,2.1, 0.1)]
+
+ y_x_2 = y_x_2 + y_x_2_2
+ #y_x_2.append(np.array([-3, 9, 0]))
+
+ plane_y_x_2 = Polygon(*y_x_2, color = RED_C, fill_color = RED_C, fill_opacity = 0.1)
+ plane_y_x_2_text = TextMobject(r"$y = x^2$", color = RED_C).move_to(np.array([5,0,2]))
+
+ ######
+
+ plane_y_2_x = Polygon(np.array([-3,5,-3]),np.array([3,-1,-3]),np.array([3,-1,3]),np.array([-3,5,3]),np.array([-3,5,-3]), color = YELLOW_C, fill_color = YELLOW_C, fill_opacity = 0.1)
+ plane_y_2_x_text = TextMobject(r"$y = 2 - x$", color = YELLOW_C).move_to(np.array([5,0,1.5]))
+
+ line_1_1 = Line(np.array([1,1,-3]), np.array([1,1,3]), color = PINK)
+
+ point = Polygon(*[np.array([0.05*np.cos(i*DEGREES),0,0.05*np.sin(i*DEGREES)]) for i in range(361)], color = "#000080", fill_color = "#000080", fill_opacity = 1).move_to(np.array([1,1,0]))
+ point_text = TextMobject(r"$(1,1,0)$", color = WHITE).scale(0.7).move_to(np.array([1.8,1,0]))
+
+
+
+
+ self.set_camera_orientation(phi=70 * DEGREES, theta = -95*DEGREES)
+
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(3.7*UP)
+
+ self.add_fixed_in_frame_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(ShowCreation(limit_func))
+ self.wait(2)
+
+ self.play(ShowCreation(plane_y_x))
+ self.add_fixed_orientation_mobjects(plane_y_x_text)
+ self.play(ShowCreation(limit_y_x))
+ self.wait()
+
+ self.play(ShowCreation(plane_y_1))
+ self.add_fixed_orientation_mobjects(plane_y_1_text)
+ self.play(ShowCreation(limit_y_1))
+ self.wait()
+
+ self.play(ShowCreation(plane_y_x_2))
+ self.add_fixed_orientation_mobjects(plane_y_x_2_text)
+ self.play(ShowCreation(limit_y_x_2))
+ self.wait()
+
+ self.play(ShowCreation(plane_y_2_x))
+ self.add_fixed_orientation_mobjects(plane_y_2_x_text)
+ self.play(ShowCreation(limit_y_2_x))
+ self.wait()
+
+ self.play(ShowCreation(line_1_1))
+ self.wait()
+
+ self.play(ShowCreation(point))
+ self.add_fixed_orientation_mobjects(point_text)
+ self.wait()
+
+ self.play(FadeOut(plane_y_x_text), FadeOut(plane_y_1_text), FadeOut(plane_y_x_2_text), FadeOut(plane_y_2_x_text))
+
+ self.move_camera(phi=0* DEGREES,theta=-95*DEGREES)
+ self.wait(2)
+ self.play(FadeOut(plane_y_x), FadeOut(plane_y_1), FadeOut(plane_y_x_2), FadeOut(plane_y_2_x))
+ self.wait(3)
+
+ self.move_camera(phi=75* DEGREES,theta=-95*DEGREES)
+ self.wait(3)
+
+
+
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file4_limit_different_point.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file4_limit_different_point.py new file mode 100644 index 0000000..0a43def --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file4_limit_different_point.py @@ -0,0 +1,115 @@ +from manimlib.imports import *
+
+class DifferentPoint(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ text3d = TextMobject(r"$f(x,y) = \frac{x^2 - y^2}{x^2 + y^2}$")
+ self.add_fixed_in_frame_mobjects(text3d)
+
+ text3d.to_corner(UL)
+
+ text3d.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+
+ self.play(Write(text3d))
+ self.wait(1)
+
+ limit_func = ParametricSurface(
+ lambda u, v: np.array([
+ 3*np.sin(u)*np.cos(v),
+ 3*np.sin(u)*np.sin(v),
+ (np.cos(v)*np.cos(v) - np.sin(v)*np.sin(v))
+ ]),u_min=0,u_max=PI,v_min=0,v_max=2*PI,checkerboard_colors=[YELLOW_C, YELLOW_E],
+ resolution=(15, 32)).scale(1)
+
+ limit_func_copy1 = limit_func.copy()
+ limit_func_copy2 = limit_func.copy()
+
+ limit_func_x = ParametricSurface(
+ lambda u, v: np.array([
+ 3*np.sin(u)*np.cos(v),
+ 3*np.sin(u)*np.sin(v),
+ (np.cos(v)*np.cos(v) - np.sin(v)*np.sin(v))
+ ]),u_min=0,u_max=PI,v_min=PI,v_max=2*PI,checkerboard_colors=[YELLOW_C, YELLOW_E],
+ resolution=(15, 32)).scale(1)
+
+ limit_func_y = ParametricSurface(
+ lambda u, v: np.array([
+ 3*np.sin(u)*np.cos(v),
+ 3*np.sin(u)*np.sin(v),
+ (np.cos(v)*np.cos(v) - np.sin(v)*np.sin(v))
+ ]),u_min=0,u_max=PI,v_min=PI/2,v_max=3*PI/2,checkerboard_colors=[YELLOW_C, YELLOW_E],
+ resolution=(15, 32)).scale(1)
+
+ limit_x =ParametricFunction(
+ lambda u : np.array([
+ u,
+ 0,
+ 1
+ ]),color="#006400",t_min=-3,t_max=3,
+ )
+
+ limit_y =ParametricFunction(
+ lambda u : np.array([
+ 0,
+ u,
+ -1
+ ]),color="#000080",t_min=-3,t_max=3,
+ )
+
+ plane_x = Polygon(np.array([-3,0,-2]),np.array([3,0,-2]),np.array([3,0,2]),np.array([-3,0,2]),np.array([-3,0,-2]), color = GREEN, fill_color = GREEN, fill_opacity = 0.2)
+ plane_x_text = TextMobject(r"$y = 0$", color = GREEN_C).move_to(1.7*UP + 3.8*RIGHT)
+
+ plane_y = Polygon(np.array([0,-3,-2]),np.array([0,3,-2]),np.array([0,3,2]),np.array([0,-3,2]),np.array([0,-3,-2]), color = BLUE, fill_color = BLUE, fill_opacity = 0.2)
+ plane_y_text = TextMobject(r"$x = 0$", color = BLUE_C).move_to(1.7*UP + 3.8*RIGHT)
+
+ origin_x = Polygon(*[np.array([0.05*np.cos(i*DEGREES),0,0.05*np.sin(i*DEGREES)]) for i in range(361)], color = "#000080", fill_color = "#000080", fill_opacity = 1).move_to(np.array([0,0,0]))
+ origin_x_text = TextMobject(r"$(0,0,0)$", color = RED_C).scale(0.7).move_to(np.array([-0.6,0,-0.5]))
+
+ origin_y = Polygon(*[np.array([0,0.05*np.cos(i*DEGREES),0.05*np.sin(i*DEGREES)]) for i in range(361)], color = "#000080", fill_color = "#000080", fill_opacity = 1).move_to(np.array([0,0,0]))
+ origin_y_text = TextMobject(r"$(0,0,0)$", color = RED_C).scale(0.7).move_to(np.array([0,-0.6,-0.5]))
+
+ self.set_camera_orientation(phi=80 * DEGREES, theta = 0*DEGREES)
+
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(3.7*UP)
+
+ self.add_fixed_in_frame_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(ShowCreation(limit_func))
+
+ self.move_camera(phi=80* DEGREES,theta=105*DEGREES)
+
+ self.play(ShowCreation(plane_x))
+ self.add_fixed_in_frame_mobjects(plane_x_text)
+ self.wait()
+ self.play(ReplacementTransform(limit_func, limit_func_x))
+ self.play(FadeOut(plane_x), FadeOut(plane_x_text), ShowCreation(origin_x))
+ self.add_fixed_orientation_mobjects(origin_x_text)
+ self.play(ShowCreation(limit_x))
+
+ self.move_camera(phi=80* DEGREES,theta=15*DEGREES)
+ self.wait(3)
+
+ self.play(FadeOut(origin_x), FadeOut(origin_x_text), FadeOut(limit_x), ReplacementTransform(limit_func_x, limit_func_copy1))
+ self.play(ShowCreation(plane_y))
+ self.add_fixed_in_frame_mobjects(plane_y_text)
+ self.wait()
+ self.play(ReplacementTransform(limit_func_copy1, limit_func_y))
+ self.play(FadeOut(plane_y), FadeOut(plane_y_text), ShowCreation(origin_y))
+ self.add_fixed_orientation_mobjects(origin_y_text)
+ self.play(ShowCreation(limit_y))
+
+ self.move_camera(phi=80* DEGREES,theta=75*DEGREES)
+ self.wait(3)
+
+ self.play(FadeOut(origin_y), FadeOut(origin_y_text), FadeOut(limit_y), ReplacementTransform(limit_func_y, limit_func_copy2))
+ self.wait(2)
+
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file5_continuity_func.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file5_continuity_func.py new file mode 100644 index 0000000..99159a4 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/file5_continuity_func.py @@ -0,0 +1,115 @@ +from manimlib.imports import *
+
+class Continuity(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ text3d = TextMobject(r"$f(x,y) = \frac{3x^2y}{x^2 + y^2}$")
+ self.add_fixed_in_frame_mobjects(text3d)
+
+ text3d.to_corner(UL)
+
+ text3d.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+
+ self.play(Write(text3d))
+ self.wait(1)
+
+
+ continuity_func = ParametricSurface(
+ lambda u, v: np.array([
+ 3*np.sin(u)*np.cos(v),
+ 3*np.sin(u)*np.sin(v),
+ 9*np.sin(u)*np.cos(v)*np.cos(v)*np.sin(v)
+ ]),u_min=0,u_max=PI,v_min=0,v_max=2*PI,checkerboard_colors=[YELLOW_C, YELLOW_E],
+ resolution=(15, 32)).scale(1)
+
+ continuity_func_copy1 = continuity_func.copy()
+ continuity_func_copy2 = continuity_func.copy()
+
+ continuity_func_x = ParametricSurface(
+ lambda u, v: np.array([
+ 3*np.sin(u)*np.cos(v),
+ 3*np.sin(u)*np.sin(v),
+ 9*np.sin(u)*np.cos(v)*np.cos(v)*np.sin(v)
+ ]),u_min=0,u_max=PI,v_min=PI,v_max=2*PI,checkerboard_colors=[YELLOW_C, YELLOW_E],
+ resolution=(15, 32)).scale(1)
+
+ continuity_func_y = ParametricSurface(
+ lambda u, v: np.array([
+ 3*np.sin(u)*np.cos(v),
+ 3*np.sin(u)*np.sin(v),
+ 9*np.sin(u)*np.cos(v)*np.cos(v)*np.sin(v)
+ ]),u_min=0,u_max=PI,v_min=PI/2,v_max=3*PI/2,checkerboard_colors=[YELLOW_C, YELLOW_E],
+ resolution=(15, 32)).scale(1)
+
+ continuity_x =ParametricFunction(
+ lambda u : np.array([
+ u,
+ 0,
+ 0
+ ]),color="#006400",t_min=-3,t_max=3,
+ )
+
+ continuity_y =ParametricFunction(
+ lambda u : np.array([
+ 0,
+ u,
+ 0
+ ]),color="#000080",t_min=-3,t_max=3,
+ )
+
+ plane_x = Polygon(np.array([-3,0,-3]),np.array([3,0,-3]),np.array([3,0,3]),np.array([-3,0,3]),np.array([-3,0,-3]), color = GREEN, fill_color = GREEN, fill_opacity = 0.2)
+ plane_x_text = TextMobject(r"$y = 0$", color = GREEN_C).move_to(1.7*UP + 3.8*RIGHT)
+
+ plane_y = Polygon(np.array([0,-3,-3]),np.array([0,3,-3]),np.array([0,3,3]),np.array([0,-3,3]),np.array([0,-3,-3]), color = BLUE, fill_color = BLUE, fill_opacity = 0.2)
+ plane_y_text = TextMobject(r"$x = 0$", color = BLUE_C).move_to(1.7*UP + 3.8*RIGHT)
+
+ origin_x = Polygon(*[np.array([0.05*np.cos(i*DEGREES),0,0.05*np.sin(i*DEGREES)]) for i in range(361)], color = "#000080", fill_color = "#000080", fill_opacity = 1).move_to(np.array([0,0,0]))
+ origin_x_text = TextMobject(r"$(0,0,0)$", color = RED_C).scale(0.7).move_to(np.array([-0.6,0,-0.5]))
+
+ origin_y = Polygon(*[np.array([0,0.05*np.cos(i*DEGREES),0.05*np.sin(i*DEGREES)]) for i in range(361)], color = "#006400", fill_color = "#006400", fill_opacity = 1).move_to(np.array([0,0,0]))
+ origin_y_text = TextMobject(r"$(0,0,0)$", color = RED_C).scale(0.7).move_to(np.array([0,-0.6,-0.5]))
+
+ self.set_camera_orientation(phi=80 * DEGREES, theta = 0*DEGREES)
+
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(3.7*UP)
+
+ self.add_fixed_in_frame_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(ShowCreation(continuity_func))
+
+ self.move_camera(phi=80* DEGREES,theta=105*DEGREES)
+
+ self.play(ShowCreation(plane_x))
+ self.add_fixed_in_frame_mobjects(plane_x_text)
+ self.wait()
+ self.play(ReplacementTransform(continuity_func, continuity_func_x))
+ self.play(FadeOut(plane_x), FadeOut(plane_x_text))
+ self.play(ShowCreation(continuity_x), ShowCreation(origin_x))
+ self.add_fixed_orientation_mobjects(origin_x_text)
+
+ self.move_camera(phi=80* DEGREES,theta=15*DEGREES)
+ self.wait(3)
+
+ self.play(FadeOut(origin_x), FadeOut(origin_x_text), FadeOut(continuity_x), ReplacementTransform(continuity_func_x, continuity_func_copy1))
+ self.play(ShowCreation(plane_y))
+ self.add_fixed_in_frame_mobjects(plane_y_text)
+ self.wait()
+ self.play(ReplacementTransform(continuity_func_copy1, continuity_func_y))
+ self.play(FadeOut(plane_y), FadeOut(plane_y_text))
+ self.play(ShowCreation(continuity_y), ShowCreation(origin_y))
+ self.add_fixed_orientation_mobjects(origin_y_text)
+
+ self.move_camera(phi=80* DEGREES,theta=75*DEGREES)
+ self.wait(3)
+
+ self.play(FadeOut(origin_y), FadeOut(origin_y_text), FadeOut(continuity_y), ReplacementTransform(continuity_func_y, continuity_func_copy2))
+ self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file1_epsilon_delta_defn.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file1_epsilon_delta_defn.gif Binary files differnew file mode 100644 index 0000000..2378bcf --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file1_epsilon_delta_defn.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file2_limit_approach_point.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file2_limit_approach_point.gif Binary files differnew file mode 100644 index 0000000..3abd596 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file2_limit_approach_point.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file3_limit_approach_point_3d.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file3_limit_approach_point_3d.gif Binary files differnew file mode 100644 index 0000000..3e87cdd --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file3_limit_approach_point_3d.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file4_limit_different_point.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file4_limit_different_point.gif Binary files differnew file mode 100644 index 0000000..9a831e4 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file4_limit_different_point.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file5_continuity_func.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file5_continuity_func.gif Binary files differnew file mode 100644 index 0000000..2a0a61f --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/multivariable-limits-and-continuity/gifs/file5_continuity_func.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/README.md b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/README.md new file mode 100644 index 0000000..c62dd51 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/README.md @@ -0,0 +1,23 @@ +**file1_partial_deriv_gas_law** + + +**file2_partial_deriv_hill** + + +**file3_partial_deriv_defn** + + +**file4_partial_deriv_example** + + +**file5_partial_deriv_func_2maximas** + + +**file6_clariant_rule** + + +**file7_partial_deriv_clariant_rule** + + +**file8_chain_rule** + diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file1_partial_deriv_gas_law.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file1_partial_deriv_gas_law.py new file mode 100644 index 0000000..3d35c97 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file1_partial_deriv_gas_law.py @@ -0,0 +1,88 @@ +from manimlib.imports import *
+
+class GasLaw(Scene):
+ def construct(self):
+ gas_law = TextMobject(r"$P$", r"$V$", r"=", r"$n$", r"$R$", r"$T$").scale(1.5)
+ gas_law[0].set_color(BLUE_C)
+ gas_law[1].set_color(GREEN_C)
+ gas_law[3].set_color(RED_C)
+ gas_law[4].set_color(ORANGE)
+ gas_law[5].set_color(YELLOW_C)
+
+ gas_law_trans = TexMobject("V", "=", "{n", "R", "T", "\\over", "P}").scale(1.5)
+ gas_law_trans[0].set_color(GREEN_C)
+ gas_law_trans[2].set_color(RED_C)
+ gas_law_trans[3].set_color(ORANGE)
+ gas_law_trans[4].set_color(YELLOW_C)
+ gas_law_trans[6].set_color(BLUE_C)
+
+ gas_law_func = TexMobject("V", "=", "f(", "n", ",", "T", ",", "P", ")").scale(1.5)
+ gas_law_func[0].set_color(GREEN_C)
+ gas_law_func[2].set_color(ORANGE)
+ gas_law_func[3].set_color(RED_C)
+ gas_law_func[5].set_color(YELLOW_C)
+ gas_law_func[7].set_color(BLUE_C)
+ gas_law_func[8].set_color(ORANGE)
+
+ partial_gas_law_func = TexMobject("{\\partial", "V","\\over", "\\partial", "P}", r"=", "{\\partial", "\\over", "\\partial", "P}", "f(", r"n", ",", r"T", ",", r"P", r")").scale(1.5)
+ partial_gas_law_func.set_color_by_tex("\\partial", PINK)
+ partial_gas_law_func.set_color_by_tex("P}", BLUE_C)
+
+ partial_gas_law_func[1].set_color(GREEN_C)
+ partial_gas_law_func[10].set_color(ORANGE)
+ partial_gas_law_func[11].set_color(RED_C)
+ partial_gas_law_func[13].set_color(YELLOW_C)
+ partial_gas_law_func[15].set_color(BLUE_C)
+ partial_gas_law_func[16].set_color(ORANGE)
+
+ partial_gas_law_trans = TexMobject("{\\partial", "V","\\over", "\\partial", "P}", r"=", "{\\partial", "\\over", "\\partial", "P}", "{n", "R", "T", "\\over", "P}").scale(1.5)
+ partial_gas_law_trans.set_color_by_tex("\\partial", PINK)
+ partial_gas_law_trans.set_color_by_tex("P}", BLUE_C)
+
+ partial_gas_law_trans[1].set_color(GREEN_C)
+ partial_gas_law_trans[10].set_color(RED_C)
+ partial_gas_law_trans[11].set_color(ORANGE)
+ partial_gas_law_trans[12].set_color(YELLOW_C)
+
+ partial_gas_law_trans2 = TexMobject("{\\partial", "V","\\over", "\\partial", "P}", r"=", "n", "R", "T", "{\\partial", "\\over", "\\partial", "P}", "P^{-1}",).scale(1.5)
+ partial_gas_law_trans2.set_color_by_tex("\\partial", PINK)
+ partial_gas_law_trans2.set_color_by_tex("P}", BLUE_C)
+
+ partial_gas_law_trans2[1].set_color(GREEN_C)
+ partial_gas_law_trans2[6].set_color(RED_C)
+ partial_gas_law_trans2[7].set_color(ORANGE)
+ partial_gas_law_trans2[8].set_color(YELLOW_C)
+ partial_gas_law_trans2[-1].set_color(BLUE_C)
+
+ partial_gas_law_trans3 = TexMobject("{\\partial", "V","\\over", "\\partial", "P}", r"=", "n", "R", "T", "P^{-2}",).scale(1.5)
+ partial_gas_law_trans3.set_color_by_tex("\\partial", PINK)
+ partial_gas_law_trans3.set_color_by_tex("P}", BLUE_C)
+
+ partial_gas_law_trans3[1].set_color(GREEN_C)
+ partial_gas_law_trans3[6].set_color(RED_C)
+ partial_gas_law_trans3[7].set_color(ORANGE)
+ partial_gas_law_trans3[8].set_color(YELLOW_C)
+ partial_gas_law_trans3[9].set_color(BLUE_C)
+
+ framebox = SurroundingRectangle(partial_gas_law_trans3, color = PURPLE, buff = 0.3)
+
+
+
+ self.play(Write(gas_law))
+ self.wait()
+ self.play(Transform(gas_law, gas_law_trans))
+ self.wait()
+ self.play(Transform(gas_law, gas_law_func))
+ self.wait()
+ self.play(Transform(gas_law, gas_law_trans))
+ self.wait()
+ self.play(Transform(gas_law, partial_gas_law_func))
+ self.wait()
+ self.play(Transform(gas_law, partial_gas_law_trans))
+ self.wait()
+ self.play(Transform(gas_law, partial_gas_law_trans2))
+ self.wait()
+ self.play(Transform(gas_law, partial_gas_law_trans3))
+ self.wait()
+ self.play(ShowCreation(framebox))
+ self.wait()
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file2_partial_deriv_hill.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file2_partial_deriv_hill.py new file mode 100644 index 0000000..bfb7687 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file2_partial_deriv_hill.py @@ -0,0 +1,122 @@ +from manimlib.imports import *
+
+class Hill(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ function = ParametricSurface(
+ lambda u, v: np.array([
+ 1.2*np.sin(u)*np.cos(v),
+ 1.2*np.sin(u)*np.sin(v),
+ -1.2*1.2*np.sin(u)*np.sin(u)*(1+0.5*np.sin(v)*np.sin(v))+2
+ ]),u_min=0,u_max=PI/2,v_min=0,v_max=2*PI,checkerboard_colors=[GREEN_C, GREEN_E],
+ resolution=(15, 32)).scale(1)
+
+ func_x =ParametricFunction(
+ lambda u : np.array([
+ u,
+ 0,
+ 2 - u*u
+ ]),color=RED_E,t_min=-1.2,t_max=1.2,
+ )
+
+ func_y =ParametricFunction(
+ lambda u : np.array([
+ 0,
+ u,
+ 2 - 1.5*u*u
+ ]),color=PINK,t_min=-1.2,t_max=1.2,
+ )
+
+ self.set_camera_orientation(phi=60 * DEGREES, theta = 0*DEGREES)
+ #self.set_camera_orientation(phi=45 * DEGREES, theta = -20*DEGREES)
+
+ self.add(axes)
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(ShowCreation(function))
+ self.wait()
+
+ self.move_camera(phi=60 * DEGREES, theta = 45*DEGREES)
+ #self.play(ShowCreation(func_x))
+
+ text_x = TextMobject("Slope of the hill along", r"$x$", "axis", color = YELLOW_C).scale(0.6).move_to(2.7*UP + 3.5*RIGHT)
+ text_x[1].set_color(PINK)
+
+
+ slope_text_x = TexMobject("Slope =", "{\\partial", "f", "\\over", "\\partial", "x}").scale(0.6).move_to(2*UP + 3.5*RIGHT)
+ slope_text_x[0].set_color(BLUE_E)
+ slope_text_x.set_color_by_tex("\\partial",YELLOW_C)
+ slope_text_x.set_color_by_tex("f",RED_E)
+ slope_text_x[5].set_color(PINK)
+
+ self.add_fixed_in_frame_mobjects(text_x, slope_text_x)
+
+ dot_x = Dot().rotate(PI/2).set_color(YELLOW_E)
+ alpha_x = ValueTracker(0)
+ vector_x = self.get_tangent_vector(alpha_x.get_value(),func_x,scale=1.5)
+ dot_x.add_updater(lambda m: m.move_to(vector_x.get_center()))
+ self.play(
+ ShowCreation(func_x),
+ GrowFromCenter(dot_x),
+ GrowArrow(vector_x)
+ )
+ vector_x.add_updater(
+ lambda m: m.become(
+ self.get_tangent_vector(alpha_x.get_value()%1,func_x,scale=1.5)
+ )
+ )
+
+ self.add(vector_x,dot_x)
+
+ self.play(alpha_x.increment_value, 1, run_time=10, rate_func=linear)
+
+ #self.move_camera(phi=60 * DEGREES, theta = 0*DEGREES)
+ self.play(FadeOut(vector_x), FadeOut(dot_x), FadeOut(func_x), FadeOut(text_x), FadeOut(slope_text_x))
+
+ text_y = TextMobject("Slope of the hill along", r"$y$", "axis", color = YELLOW_C).scale(0.6).move_to(2.7*UP + 3.5*RIGHT)
+ text_y[1].set_color(RED_C)
+
+
+ slope_text_y = TexMobject("Slope =", "{\\partial", "f", "\\over", "\\partial", "x}").scale(0.6).move_to(2*UP + 3.5*RIGHT)
+ slope_text_y[0].set_color(BLUE_E)
+ slope_text_y.set_color_by_tex("\\partial",YELLOW_C)
+ slope_text_y.set_color_by_tex("f",PINK)
+ slope_text_y[5].set_color(RED_C)
+
+ self.add_fixed_in_frame_mobjects(text_y, slope_text_y)
+
+ dot_y = Dot().rotate(PI/2).set_color(BLUE_E)
+ alpha_y = ValueTracker(0)
+ vector_y = self.get_tangent_vector(alpha_y.get_value(),func_y,scale=1.5)
+ dot_y.add_updater(lambda m: m.move_to(vector_y.get_center()))
+ self.play(
+ ShowCreation(func_y),
+ GrowFromCenter(dot_y),
+ GrowArrow(vector_y)
+ )
+ vector_y.add_updater(
+ lambda m: m.become(
+ self.get_tangent_vector(alpha_y.get_value()%1,func_y,scale=1.5)
+ )
+ )
+
+ self.add(vector_y,dot_y)
+ self.play(alpha_y.increment_value, 1, run_time=10, rate_func=linear)
+ self.play(FadeOut(vector_y), FadeOut(dot_y), FadeOut(func_y), FadeOut(text_y), FadeOut(slope_text_y))
+ self.wait(2)
+
+ def get_tangent_vector(self, proportion, curve, dx=0.001, scale=1):
+ coord_i = curve.point_from_proportion(proportion)
+ coord_f = curve.point_from_proportion(proportion + dx)
+ reference_line = Line(coord_i,coord_f)
+ unit_vector = reference_line.get_unit_vector() * scale
+ vector = Line(coord_i - unit_vector, coord_i + unit_vector, color = ORANGE, buff=0)
+ return vector
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file3_partial_deriv_defn.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file3_partial_deriv_defn.py new file mode 100644 index 0000000..a25ca56 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file3_partial_deriv_defn.py @@ -0,0 +1,218 @@ +from manimlib.imports import *
+
+class PartialDeriv(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ paraboloid = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ -2*2*np.sin(u)*np.sin(u)+2
+ ]),u_min=0,u_max=PI/2,v_min=0,v_max=2*PI,checkerboard_colors=[PINK, PURPLE],
+ resolution=(15, 32)).scale(1)
+
+ paraboloid_copy1 = paraboloid.copy()
+ paraboloid_copy2 = paraboloid.copy()
+
+ paraboloid_x = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ -2*2*np.sin(u)*np.sin(u)+2
+ ]),u_min=0,u_max=PI/2,v_min=PI,v_max=2*PI,checkerboard_colors=[PINK, PURPLE],
+ resolution=(15, 32)).scale(1)
+
+ paraboloid_x_copy = paraboloid_x.copy()
+
+ paraboloid_y = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ -2*2*np.sin(u)*np.sin(u)+2
+ ]),u_min=0,u_max=PI/2,v_min=PI/2,v_max=3*PI/2,checkerboard_colors=[PINK, PURPLE],
+ resolution=(15, 32)).scale(1)
+
+ parabola1 =ParametricFunction(
+ lambda u : np.array([
+ u,
+ 0,
+ -(u*u) + 2
+ ]),color="#006400",t_min=-2,t_max=2,
+ )
+ parabola2 =ParametricFunction(
+ lambda u : np.array([
+ 0,
+ u,
+ -(u*u) + 2
+ ]),color=BLUE_C,t_min=-2,t_max=2,
+ )
+
+ plane1 = Polygon(np.array([-2.2,0,-2.5]),np.array([2.2,0,-2.5]),np.array([2.2,0,2.5]),np.array([-2.2,0,2.5]),np.array([-2.2,0,-2.5]), color = GREEN, fill_color = GREEN, fill_opacity = 0.2)
+ plane1_text = TextMobject(r"$y = 0$", color = GREEN_C).move_to(2*UP + 3.3*RIGHT)
+
+ plane2 = Polygon(np.array([0,-2.2,-2.5]),np.array([0,2.2,-2.5]),np.array([0,2.2,2.5]),np.array([0,-2.2,2.5]),np.array([0,-2.2,-2.5]), color = BLUE, fill_color = BLUE, fill_opacity = 0.2)
+ plane2_text = TextMobject(r"$x = 0$", color = BLUE_C).move_to(2*UP + 3.2*RIGHT)
+
+ surface_eqn = TextMobject("Surface", r"$z = 2- x^2 -y^2$", color = YELLOW_C).scale(0.6).move_to(np.array([3*LEFT +3*UP]))
+ surface_eqn[0].set_color(PINK)
+
+ dot1 =Sphere(radius=0.08).move_to(np.array([-1,0,1]))
+ dot1.set_fill(RED)
+ line1 = Line(np.array([-1.55, 0,0]), np.array([-0.4, 0,2.2]), color = RED)
+ lab_x = TextMobject(r"$f(x_0,y_0)$", color = RED).scale(0.7)
+ para_lab_x = TextMobject(r"$f(x,y_0)$", color = "#006400").scale(0.7)
+ tangent_line_x = TextMobject("Tangent Line", color = RED_C, buff = 0.4).scale(0.6).move_to(np.array([1.7*RIGHT +1.8*UP]))
+
+
+ text1 = TextMobject(r"$\frac{\partial f}{\partial x}\vert_{(x_0,y_0)} = \frac{d}{dx}$", r"$f(x,y_0)$", r"$\vert_{x=x_0}$").scale(0.6)
+ brace1 = Brace(text1[1], DOWN, buff = SMALL_BUFF, color = GREEN)
+ t1 = brace1.get_text("Just depends on x")
+ t1.scale(0.6)
+ t1.set_color(GREEN)
+
+
+ dot2 =Sphere(radius=0.08).move_to(np.array([0,1,1]))
+ dot2.set_fill(RED)
+ line2 = Line(np.array([0, 1.55,0]), np.array([0, 0.4,2.2]), color = RED)
+ lab_y = TextMobject(r"$f(x_0,y_0)$", color = RED).scale(0.7)
+ para_lab_y = TextMobject(r"$f(x_0,y)$", color = BLUE_C).scale(0.7)
+ tangent_line_y = TextMobject("Tangent Line", color = RED_C, buff = 0.4).scale(0.6).move_to(np.array([1.7*RIGHT +1.8*UP]))
+
+ text2 = TextMobject(r"$\frac{\partial f}{\partial y}\vert_{(x_0,y_0)} = \frac{d}{dy}$", r"$f(x_0,y)$", r"$\vert_{y=y_0}$").scale(0.6)
+ brace2 = Brace(text2[1], DOWN, buff = SMALL_BUFF, color = GREEN)
+ t2 = brace2.get_text("Just depends on y")
+ t2.scale(0.6)
+ t2.set_color(GREEN)
+
+ text3 = TextMobject(r"$= \lim_{h \to 0} \frac{f(x_0+h,y_0) - f(x_0,y_0)}{h}$").scale(0.6)
+
+ dot3 =Sphere(radius=0.08).move_to(np.array([-1.22,0,0.5]))
+ dot3.set_fill(YELLOW_C)
+ line3 = Line(np.array([-1.44,0,0]), np.array([-0.6,0,2.2]), color = YELLOW_C)
+ lab_line3 = TextMobject(r"$f(x_0+h,y_0)$", color = YELLOW_C).scale(0.7)
+
+
+ self.set_camera_orientation(phi=80 * DEGREES, theta = 0*DEGREES)
+ #self.set_camera_orientation(phi=80 * DEGREES, theta = 20*DEGREES)
+ #self.begin_ambient_camera_rotation(rate=0.3)
+
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(3.7*UP)
+
+ self.add_fixed_in_frame_mobjects(axis[2])
+ #self.add_fixed_orientation_mobjects(axis[2])
+
+ self.play(Write(paraboloid))
+
+ self.add_fixed_in_frame_mobjects(surface_eqn)
+ #self.move_camera(phi=80* DEGREES,theta=110*DEGREES)
+ self.move_camera(phi=80* DEGREES,theta=45*DEGREES)
+
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+ self.play(ShowCreation(plane1))
+ self.add_fixed_in_frame_mobjects(plane1_text)
+ self.wait()
+ self.play(ReplacementTransform(paraboloid, paraboloid_x))
+
+ lab_x.move_to(np.array([1.8*RIGHT +1.15*UP]))
+ para_lab_x.move_to(np.array([1.3*LEFT +1.6*UP]))
+ self.wait()
+ self.play(FadeOut(plane1), FadeOut(plane1_text))
+ self.play(ShowCreation(parabola1))
+ self.add_fixed_in_frame_mobjects(para_lab_x)
+ self.play(ShowCreation(dot1))
+ self.add_fixed_in_frame_mobjects(lab_x)
+ #self.play(ShowCreation(dot1))
+ self.wait()
+ self.play(ShowCreation(line1))
+ self.add_fixed_in_frame_mobjects(tangent_line_x)
+ self.wait()
+
+ self.add_fixed_in_frame_mobjects(text1, brace1, t1)
+ grp1 = VGroup(text1, brace1, t1)
+ grp1.move_to(3*UP+3*RIGHT)
+ self.play(Write(text1),GrowFromCenter(brace1), FadeIn(t1))
+ self.wait()
+ self.play(FadeOut(parabola1), FadeOut(line1), FadeOut(lab_x), FadeOut(para_lab_x), FadeOut(dot1), FadeOut(tangent_line_x),FadeOut(grp1))
+
+
+
+
+ #self.move_camera(phi=80* DEGREES,theta=20*DEGREES)
+
+ self.play(ReplacementTransform(paraboloid_x, paraboloid_copy1))
+ self.wait()
+ self.play(ShowCreation(plane2))
+ self.add_fixed_in_frame_mobjects(plane2_text)
+ self.wait()
+ self.play(ReplacementTransform(paraboloid_copy1, paraboloid_y))
+
+ lab_y.move_to(np.array([1.8*RIGHT +1.15*UP]))
+ para_lab_y.move_to(np.array([1.3*LEFT +1.6*UP]))
+ self.wait()
+ self.play(FadeOut(plane2), FadeOut(plane2_text))
+ self.play(ShowCreation(parabola2))
+ self.add_fixed_in_frame_mobjects(para_lab_y)
+ self.play(ShowCreation(dot2))
+ self.add_fixed_in_frame_mobjects(lab_y)
+ self.wait()
+ self.play(ShowCreation(line2))
+ self.add_fixed_in_frame_mobjects(tangent_line_y)
+ self.wait()
+
+ self.add_fixed_in_frame_mobjects(text2, brace2, t2)
+ grp2 = VGroup(text2, brace2, t2)
+ grp2.move_to(3*UP+3*RIGHT)
+ self.play(Write(text2),GrowFromCenter(brace2), FadeIn(t2))
+ self.wait()
+ self.play(FadeOut(parabola2), FadeOut(line2), FadeOut(lab_y), FadeOut(para_lab_y), FadeOut(dot2), FadeOut(tangent_line_y), FadeOut(grp2))
+ self.wait()
+
+
+ #self.move_camera(phi=80* DEGREES,theta=105*DEGREES)
+ self.play(ReplacementTransform(paraboloid_y, paraboloid_copy2))
+ self.wait()
+
+
+ self.play(ShowCreation(plane1))
+ self.add_fixed_in_frame_mobjects(plane1_text)
+ self.wait()
+ self.play(ReplacementTransform(paraboloid_copy2, paraboloid_x_copy))
+
+ lab_x.move_to(np.array([1.8*RIGHT +1.15*UP]))
+ para_lab_x.move_to(np.array([1.3*LEFT +1.6*UP]))
+ lab_line3.move_to(np.array([2.4*RIGHT +0.5*UP]))
+ self.wait()
+ self.play(FadeOut(plane1), FadeOut(plane1_text))
+ self.play(ShowCreation(parabola1))
+ self.add_fixed_in_frame_mobjects(para_lab_x)
+ self.play(ShowCreation(dot1))
+ self.add_fixed_in_frame_mobjects(lab_x)
+ self.play(ShowCreation(dot3))
+ self.add_fixed_in_frame_mobjects(lab_line3)
+ self.wait()
+ self.play(ShowCreation(line1))
+ self.add_fixed_in_frame_mobjects(tangent_line_x)
+ self.play(ShowCreation(line3))
+ self.wait()
+
+
+ self.add_fixed_in_frame_mobjects(text1,text3)
+ text1.move_to(3*UP+3*RIGHT)
+ text3.next_to(text1, DOWN)
+ self.play(Write(text1),Write(text3))
+ self.wait()
+ self.play(FadeOut(parabola1), FadeOut(line1), FadeOut(lab_x), FadeOut(line3), FadeOut(lab_line3), FadeOut(para_lab_x), FadeOut(dot1), FadeOut(dot3), FadeOut(tangent_line_x), FadeOut(text1), FadeOut(text3))
+ self.wait()
+
+
+
+
+
diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file4_partial_deriv_example.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file4_partial_deriv_example.py new file mode 100644 index 0000000..5712a62 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file4_partial_deriv_example.py @@ -0,0 +1,246 @@ +from manimlib.imports import *
+
+class PartialDerivX(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ paraboloid = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ -2*2*np.sin(u)*np.sin(u)+2
+ ]),u_min=0,u_max=PI/2,v_min=0,v_max=2*PI,checkerboard_colors=[PINK, PURPLE],
+ resolution=(15, 32)).scale(1)
+
+ paraboloid_copy = paraboloid.copy()
+
+
+ paraboloid_x = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ -2*2*np.sin(u)*np.sin(u)+2
+ ]),u_min=0,u_max=PI/2,v_min=PI,v_max=2*PI,checkerboard_colors=[PINK, PURPLE],
+ resolution=(15, 32)).scale(1)
+
+
+ parabola =ParametricFunction(
+ lambda u : np.array([
+ u,
+ 0,
+ -(u*u) + 2
+ ]),color="#006400",t_min=-2,t_max=2,
+ )
+
+ plane = Polygon(np.array([-2.2,0,-2.5]),np.array([2.2,0,-2.5]),np.array([2.2,0,2.5]),np.array([-2.2,0,2.5]),np.array([-2.2,0,-2.5]), color = GREEN, fill_color = GREEN, fill_opacity = 0.2)
+ plane_text = TextMobject(r"$y = 0$", color = GREEN_C).move_to(2*UP + 3*RIGHT)
+
+ surface_eqn = TextMobject("Surface", r"$z = 2- x^2 -y^2$", color = PINK).scale(0.6).move_to(np.array([3*LEFT +3*UP]))
+ surface_eqn[0].set_color(BLUE_C)
+
+ line = Line(np.array([-2,0,0]), np.array([2,0,0]), color = RED_C)
+
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(3.7*UP)
+
+ self.add_fixed_in_frame_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+
+ self.set_camera_orientation(phi=80 * DEGREES, theta = 0*DEGREES)
+
+ self.play(Write(paraboloid))
+
+ self.add_fixed_in_frame_mobjects(surface_eqn)
+ #self.move_camera(phi=80* DEGREES,theta=95*DEGREES)
+ self.move_camera(phi=80* DEGREES,theta=45*DEGREES)
+ self.play(ShowCreation(plane))
+ self.add_fixed_in_frame_mobjects(plane_text)
+ self.wait()
+ self.play(ReplacementTransform(paraboloid, paraboloid_x))
+ self.play(FadeOut(plane), FadeOut(plane_text))
+ self.play(ShowCreation(parabola), ShowCreation(line))
+
+ text1 = TextMobject("Moving small", r"$dx$", r"steps").scale(0.6).move_to(3*UP + 3.5*RIGHT).set_color_by_gradient(RED, ORANGE, YELLOW, BLUE, PURPLE)
+
+ text2 = TextMobject("Observing change in function, keeping", r"$y$", r"constant").scale(0.6).move_to(2.6*UP + 3.5*RIGHT).set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+
+ slope_text = TexMobject("Slope =", "{\\partial", "f", "\\over", "\\partial", "x}").scale(0.6).move_to(2*UP + 3.5*RIGHT)
+ slope_text[0].set_color(BLUE_E)
+ slope_text.set_color_by_tex("\\partial",PINK)
+ slope_text.set_color_by_tex("f","#006400")
+ slope_text[5].set_color(RED_C)
+
+ self.add_fixed_in_frame_mobjects(text1, text2)
+ self.wait()
+ self.add_fixed_in_frame_mobjects(slope_text)
+ #add_fixed_orientation_mobjects
+
+
+ dot = Dot().rotate(PI/2).set_color(RED_C)
+ alpha = ValueTracker(0)
+ vector = self.get_tangent_vector(alpha.get_value(),parabola,scale=1.5)
+ dot.add_updater(lambda m: m.move_to(vector.get_center()))
+ self.play(
+ ShowCreation(parabola),
+ GrowFromCenter(dot),
+ GrowArrow(vector)
+ )
+ vector.add_updater(
+ lambda m: m.become(
+ self.get_tangent_vector(alpha.get_value()%1,parabola,scale=1.5)
+ )
+ )
+ self.add(vector,dot)
+ self.play(alpha.increment_value, 1, run_time=10, rate_func=linear)
+ self.wait()
+
+
+ '''
+ for i in np.arange(-2,2,0.2):
+ self.play(ReplacementTransform(Line(np.array([i,0,0]), np.array([i,0,-i*i + 2]), color = GREEN_C), Line(np.array([i+0.2,0,0]), np.array([i+0.2,0,-(i+0.2)**2 + 2]), color = GREEN_C)))
+ #self.wait()
+ '''
+
+ self.wait()
+ self.play(FadeOut(parabola), FadeOut(line), FadeOut(vector), FadeOut(dot), FadeOut(text1), FadeOut(text2), FadeOut(slope_text),FadeOut(surface_eqn))
+
+ #self.move_camera(phi=80* DEGREES,theta= 0*DEGREES)
+ self.play(ReplacementTransform(paraboloid_x, paraboloid_copy))
+ self.wait()
+
+
+ def get_tangent_vector(self, proportion, curve, dx=0.001, scale=1):
+ coord_i = curve.point_from_proportion(proportion)
+ coord_f = curve.point_from_proportion(proportion + dx)
+ reference_line = Line(coord_i,coord_f)
+ unit_vector = reference_line.get_unit_vector() * scale
+ vector = Line(coord_i - unit_vector, coord_i + unit_vector, color = BLUE_E, buff=0)
+ return vector
+
+
+class PartialDerivY(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ paraboloid = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ -2*2*np.sin(u)*np.sin(u)+2
+ ]),u_min=0,u_max=PI/2,v_min=0,v_max=2*PI,checkerboard_colors=[PINK, PURPLE],
+ resolution=(15, 32)).scale(1)
+
+ paraboloid_copy = paraboloid.copy()
+
+
+ paraboloid_y = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ -2*2*np.sin(u)*np.sin(u)+2
+ ]),u_min=0,u_max=PI/2,v_min=PI/2,v_max=3*PI/2,checkerboard_colors=[PINK, PURPLE],
+ resolution=(15, 32)).scale(1)
+
+
+ parabola =ParametricFunction(
+ lambda u : np.array([
+ 0,
+ u,
+ -(u*u) + 2
+ ]),color=YELLOW_C,t_min=-2,t_max=2,
+ )
+
+ plane = Polygon(np.array([0,-2.2,-2.5]),np.array([0,2.2,-2.5]),np.array([0,2.2,2.5]),np.array([0,-2.2,2.5]),np.array([0,-2.2,-2.5]), color = BLUE, fill_color = BLUE, fill_opacity = 0.2)
+ plane_text = TextMobject(r"$x = 0$", color = BLUE_C).move_to(2*UP + 3*RIGHT)
+
+ surface_eqn = TextMobject("Surface", r"$z = 2- x^2 -y^2$", color = PINK).scale(0.6).move_to(np.array([3*LEFT +3*UP]))
+ surface_eqn[0].set_color(BLUE_C)
+
+ line = Line(np.array([0,-2,0]), np.array([0,2,0]), color = RED_C)
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(3.7*UP)
+
+ self.add_fixed_in_frame_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.set_camera_orientation(phi=80 * DEGREES, theta = 45*DEGREES)
+
+ self.play(Write(paraboloid))
+
+ self.add_fixed_in_frame_mobjects(surface_eqn)
+ #self.move_camera(phi=80* DEGREES,theta=5*DEGREES)
+ self.play(ShowCreation(plane))
+ self.add_fixed_in_frame_mobjects(plane_text)
+ self.wait()
+ self.play(ReplacementTransform(paraboloid, paraboloid_y))
+ self.play(FadeOut(plane), FadeOut(plane_text))
+ self.play(ShowCreation(parabola), ShowCreation(line))
+
+ text1 = TextMobject("Moving small", r"$dy$", r"steps").scale(0.6).move_to(3*UP + 3.5*RIGHT).set_color_by_gradient(RED, ORANGE, YELLOW, BLUE, PURPLE)
+
+ text2 = TextMobject("Observing change in function, keeping", r"$x$", r"constant").scale(0.6).move_to(2.6*UP + 3.5*RIGHT).set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+
+ slope_text = TexMobject("Slope =", "{\\partial", "f", "\\over", "\\partial", "y}").scale(0.6).move_to(2*UP + 3.5*RIGHT)
+ slope_text[0].set_color("#006400")
+ slope_text.set_color_by_tex("\\partial",PINK)
+ slope_text.set_color_by_tex("f",YELLOW_C)
+ slope_text[5].set_color(RED_C)
+
+ self.add_fixed_in_frame_mobjects(text1, text2)
+ self.wait()
+ self.add_fixed_in_frame_mobjects(slope_text)
+
+ dot = Dot().rotate(PI/2).set_color(RED_C)
+ alpha = ValueTracker(0)
+ vector = self.get_tangent_vector(alpha.get_value(),parabola,scale=1.5)
+ dot.add_updater(lambda m: m.move_to(vector.get_center()))
+ self.play(
+ ShowCreation(parabola),
+ GrowFromCenter(dot),
+ GrowArrow(vector)
+ )
+ vector.add_updater(
+ lambda m: m.become(
+ self.get_tangent_vector(alpha.get_value()%1,parabola,scale=1.5)
+ )
+ )
+ self.add(vector,dot)
+ self.play(alpha.increment_value, 1, run_time=10, rate_func=linear)
+ self.wait()
+
+ '''
+ for i in np.arange(-2,2,0.2):
+ self.play(ReplacementTransform(Line(np.array([0,i,0]), np.array([0,i,-i*i + 2]), color = BLUE_C), Line(np.array([0,i+0.2,0]), np.array([0,i+0.2,-(i+0.2)**2 + 2]), color = BLUE_C)))
+ #self.wait()
+ '''
+
+
+ self.wait()
+ self.play(FadeOut(parabola), FadeOut(line), FadeOut(vector), FadeOut(dot), FadeOut(text1), FadeOut(text2), FadeOut(slope_text),FadeOut(surface_eqn))
+
+ #self.move_camera(phi=80* DEGREES,theta= 90*DEGREES)
+ self.play(ReplacementTransform(paraboloid_y, paraboloid_copy))
+ self.wait()
+
+ def get_tangent_vector(self, proportion, curve, dx=0.001, scale=1):
+ coord_i = curve.point_from_proportion(proportion)
+ coord_f = curve.point_from_proportion(proportion + dx)
+ reference_line = Line(coord_i,coord_f)
+ unit_vector = reference_line.get_unit_vector() * scale
+ vector = Line(coord_i - unit_vector, coord_i + unit_vector, color = "#006400", buff=0)
+ return vector
+
+
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file5_partial_deriv_func_2maximas.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file5_partial_deriv_func_2maximas.py new file mode 100644 index 0000000..7bbb9a7 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file5_partial_deriv_func_2maximas.py @@ -0,0 +1,227 @@ +from manimlib.imports import *
+
+class MaximaMinima(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ paraboloid = ParametricSurface(
+ lambda u, v: np.array([
+ 3.5*np.sin(u)*np.cos(v),
+ 3.5*np.sin(u)*np.sin(v),
+ 3.5*3.5*np.sin(u)*np.sin(u)*(1+2*np.sin(v)*np.sin(v))*np.exp(1 - 3.5*3.5*np.sin(u)*np.sin(u) )
+ ]),u_min=0,u_max=PI,v_min=0,v_max=2*PI, color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.1,
+ resolution=(15, 32)).scale(1)
+
+ paraboloid_copy1 = paraboloid.copy()
+ paraboloid_copy2 = paraboloid.copy()
+
+ paraboloid_x = ParametricSurface(
+ lambda u, v: np.array([
+ 3.5*np.sin(u)*np.cos(v),
+ 3.5*np.sin(u)*np.sin(v),
+ 3.5*3.5*np.sin(u)*np.sin(u)*(1+2*np.sin(v)*np.sin(v))*np.exp(1 - 3.5*3.5*np.sin(u)*np.sin(u) )
+ ]),u_min=0,u_max=PI,v_min=PI,v_max=2*PI, color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.1,
+ resolution=(15, 32)).scale(1)
+
+ paraboloid_y = ParametricSurface(
+ lambda u, v: np.array([
+ 3.5*np.sin(u)*np.cos(v),
+ 3.5*np.sin(u)*np.sin(v),
+ 3.5*3.5*np.sin(u)*np.sin(u)*(1+2*np.sin(v)*np.sin(v))*np.exp(1 - 3.5*3.5*np.sin(u)*np.sin(u) )
+ ]),u_min=0,u_max=PI,v_min=PI/2,v_max=3*PI/2, color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.1,
+ resolution=(15, 32)).scale(1)
+
+ parabola_x_out =ParametricFunction(
+ lambda u : np.array([
+ u,
+ 0,
+ (u*u )*np.exp(1-u*u)
+ ]),color=RED_E,t_min=-3.5,t_max=3.5,
+ )
+
+ parabola_y_out =ParametricFunction(
+ lambda u : np.array([
+ 0,
+ u,
+ (3*u*u)*np.exp(1-u*u)
+ ]),color=PINK,t_min=-3.5,t_max=3.5,
+ )
+
+ plane1 = Polygon(np.array([-3.5,0,-3]),np.array([3.5,0,-3]),np.array([3.5,0,3]),np.array([-3.5,0,3]),np.array([-3.5,0,-3]), color = RED_C, fill_color = RED_C, fill_opacity = 0.2)
+ plane_text_x = TextMobject(r"$y = 0$", color = RED_C).move_to(2*UP + 4.5*RIGHT)
+
+ plane2 = Polygon(np.array([0,-3.5,-3]),np.array([0,3.5,-3]),np.array([0,3.5,3]),np.array([0,-3.5,3]),np.array([0,-3.5,-3]), color = PINK, fill_color = PINK, fill_opacity = 0.2)
+ plane_text_y = TextMobject(r"$x = 0$", color = PINK).move_to(2*UP + 4.5*RIGHT)
+
+ surface_eqn = TextMobject("Surface", r"$z = (x^2 + 3y^2)e^{(1 - x^2 - y^2)}$", color = YELLOW_C).scale(0.6).move_to(np.array([3.5*LEFT +3.5*UP]))
+ surface_eqn[0].set_color(BLUE_C)
+
+ self.set_camera_orientation(phi=60 * DEGREES, theta = 45*DEGREES)
+
+ self.add(axes)
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(ShowCreation(paraboloid))
+
+
+ #self.move_camera(phi=60 * DEGREES, theta = 45*DEGREES,run_time=3)
+
+
+ plane_x = Polygon(np.array([-3.5,2,-3]),np.array([3.5,2,-3]),np.array([3.5,2,3]),np.array([-3.5,2,3]),np.array([-3.5,2,-3]), color = YELLOW_C, fill_color = YELLOW_A, fill_opacity = 0.2)
+
+ plane_y = Polygon(np.array([2,-3.5,-3]),np.array([2,3.5,-3]),np.array([2,3.5,3]),np.array([2,-3.5,3]),np.array([2,-3.5,-3]), color = GREEN_C, fill_color = GREEN_A, fill_opacity = 0.2)
+
+ text_x = TextMobject(r"$x$", "is fixed on this" ,"plane").scale(0.7).to_corner(UL)
+ text_y = TextMobject(r"$y$", "is fixed on this" ,"plane").scale(0.7).to_corner(UR)
+
+ text_x[0].set_color(RED_C)
+ text_y[0].set_color(PINK)
+ text_x[1].set_color(BLUE_C)
+ text_y[1].set_color(BLUE_C)
+ text_x[2].set_color(GREEN_C)
+ text_y[2].set_color(YELLOW_C)
+
+ self.add_fixed_in_frame_mobjects(text_x, text_y)
+
+ for i in range(2,-4,-1):
+
+ parabola_x =ParametricFunction(lambda u : np.array([u,i,(u*u + 3*i*i)*np.exp(1- u*u - i*i)]),color=RED_C,t_min=-3.5,t_max=3.5,)
+
+ parabola_y =ParametricFunction(lambda u : np.array([i,u,(i*i + 3*u*u)*np.exp(1- u*u - i*i)]),color=PINK,t_min=-3.5,t_max=3.5,)
+
+ if(i==2):
+ self.play(ShowCreation(plane_x), ShowCreation(plane_y))
+ parabola_copy_x = parabola_x.copy()
+ parabola_copy_y = parabola_y.copy()
+
+
+ self.play(ShowCreation(parabola_copy_x), ShowCreation(parabola_copy_y))
+ self.wait()
+ self.play(FadeOut(parabola_copy_x), FadeOut(parabola_copy_y))
+
+ else:
+ self.play(ApplyMethod(plane_x.move_to, np.array([0,i,0])),ReplacementTransform(parabola_copy_x, parabola_x),ApplyMethod(plane_y.move_to, np.array([i,0,0])),ReplacementTransform(parabola_copy_y, parabola_y))
+ self.play(FadeOut(parabola_x), FadeOut(parabola_y))
+ self.wait()
+
+ parabola_copy_x = parabola_x.copy()
+ parabola_copy_y = parabola_y.copy()
+
+ self.play(FadeOut(plane_x), FadeOut(plane_y), FadeOut(text_x), FadeOut(text_y))
+
+
+ self.add_fixed_in_frame_mobjects(surface_eqn)
+
+ self.move_camera(phi=80 * DEGREES, theta = 95*DEGREES)
+
+ self.play(ShowCreation(plane1))
+ self.add_fixed_in_frame_mobjects(plane_text_x)
+ self.wait()
+ self.play(ReplacementTransform(paraboloid, paraboloid_x))
+ self.play(FadeOut(plane1), FadeOut(plane_text_x))
+
+ line_x = Line(np.array([-3.5,0,0]), np.array([3.5,0,0]), color = YELLOW_E)
+
+ self.play(ShowCreation(parabola_x_out), ShowCreation(line_x))
+
+ slope_text_x = TexMobject("Slope =", "{\\partial", "f", "\\over", "\\partial", "x}").scale(0.6).move_to(2*UP + 3.5*RIGHT)
+ slope_text_x[0].set_color(ORANGE)
+ slope_text_x.set_color_by_tex("\\partial",GREEN_E)
+ slope_text_x.set_color_by_tex("f",RED_E)
+ slope_text_x[5].set_color(YELLOW_E)
+
+ self.add_fixed_in_frame_mobjects(slope_text_x)
+
+
+ dot_x = Dot().rotate(PI/2).set_color(YELLOW_E)
+ alpha_x = ValueTracker(0)
+ vector_x = self.get_tangent_vector(alpha_x.get_value(),parabola_x_out,scale=1.5)
+ dot_x.add_updater(lambda m: m.move_to(vector_x.get_center()))
+ self.play(
+ ShowCreation(parabola_x_out),
+ GrowFromCenter(dot_x),
+ GrowArrow(vector_x)
+ )
+ vector_x.add_updater(
+ lambda m: m.become(
+ self.get_tangent_vector(alpha_x.get_value()%1,parabola_x_out,scale=1.5)
+ )
+ )
+ self.add(vector_x,dot_x)
+ self.play(alpha_x.increment_value, 1, run_time=10, rate_func=linear)
+
+ self.wait(2)
+ self.play(FadeOut(parabola_x_out), FadeOut(line_x), FadeOut(vector_x), FadeOut(dot_x), FadeOut(slope_text_x))
+
+ self.move_camera(phi=80* DEGREES,theta= 5*DEGREES)
+ self.play(ReplacementTransform(paraboloid_x, paraboloid_copy1))
+ self.wait()
+
+
+
+ self.play(ShowCreation(plane2))
+ self.add_fixed_in_frame_mobjects(plane_text_y)
+ self.wait()
+ self.play(ReplacementTransform(paraboloid_copy1, paraboloid_y))
+ self.play(FadeOut(plane2), FadeOut(plane_text_y))
+
+ line_y = Line(np.array([0,-3.5,0]), np.array([0,3.5,0]), color = GREEN_E)
+
+ self.play(ShowCreation(parabola_y_out), ShowCreation(line_y))
+
+ slope_text_y = TexMobject("Slope =", "{\\partial", "f", "\\over", "\\partial", "y}").scale(0.6).move_to(2*UP + 3.5*RIGHT)
+ slope_text_y[0].set_color(ORANGE)
+ slope_text_y.set_color_by_tex("\\partial",YELLOW_E)
+ slope_text_y.set_color_by_tex("f",PINK)
+ slope_text_y[5].set_color(GREEN_E)
+
+ self.add_fixed_in_frame_mobjects(slope_text_y)
+
+
+ dot_y = Dot().rotate(PI/2).set_color(GREEN_E)
+ alpha_y = ValueTracker(0)
+ vector_y = self.get_tangent_vector(alpha_y.get_value(),parabola_y_out,scale=1.5)
+ dot_y.add_updater(lambda m: m.move_to(vector_y.get_center()))
+ self.play(
+ ShowCreation(parabola_y_out),
+ GrowFromCenter(dot_y),
+ GrowArrow(vector_y)
+ )
+ vector_y.add_updater(
+ lambda m: m.become(
+ self.get_tangent_vector(alpha_y.get_value()%1,parabola_y_out,scale=1.5)
+ )
+ )
+ self.add(vector_y,dot_y)
+ self.play(alpha_y.increment_value, 1, run_time=10, rate_func=linear)
+
+ self.wait(2)
+ self.play(FadeOut(parabola_y_out), FadeOut(line_y), FadeOut(vector_y), FadeOut(dot_y), FadeOut(slope_text_y))
+
+ self.move_camera(phi=60* DEGREES,theta= 45*DEGREES)
+ self.play(ReplacementTransform(paraboloid_y, paraboloid_copy2))
+ self.wait()
+
+
+
+
+
+
+
+
+
+ def get_tangent_vector(self, proportion, curve, dx=0.001, scale=1):
+ coord_i = curve.point_from_proportion(proportion)
+ coord_f = curve.point_from_proportion(proportion + dx)
+ reference_line = Line(coord_i,coord_f)
+ unit_vector = reference_line.get_unit_vector() * scale
+ vector = Line(coord_i - unit_vector , coord_i + unit_vector, color = ORANGE, buff=0)
+ return vector
+
diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file6_clariant_rule.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file6_clariant_rule.py new file mode 100644 index 0000000..b79f77c --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file6_clariant_rule.py @@ -0,0 +1,64 @@ +from manimlib.imports import *
+
+class ClariantRule(Scene):
+ def construct(self):
+ derivatives = TextMobject(r"$cos(x)y^3$",r"$-sin(x)y^3$", r"$3cos(x)y^2$", r"$-cos(x)y^3$", r"$-3sin(x)y^2$", r"$-3sin(x)y^2$", r"$6cos(x)y$")
+
+ partial_derivatives = TextMobject(r"$\frac{\partial}{\partial x}$", r"$\frac{\partial}{\partial y}$")
+
+
+ derivatives[0].move_to(2*UP).set_color(PURPLE)
+ derivatives[1].move_to(3*LEFT).set_color(YELLOW_C)
+ derivatives[2].move_to(3*RIGHT).set_color(BLUE_C)
+
+ arrrow_1 = Arrow(derivatives[0].get_bottom(), derivatives[1].get_top())
+ arrrow_1_lab = partial_derivatives[0].copy().scale(0.7)
+ arrrow_1_lab.move_to(2.5*LEFT+ 1.3*UP)
+
+ arrrow_2 = Arrow(derivatives[0].get_bottom(), derivatives[2].get_top())
+ arrrow_2_lab = partial_derivatives[1].copy().scale(0.7)
+ arrrow_2_lab.move_to(2.5*RIGHT+ 1.3*UP)
+
+ self.play(Write(derivatives[0]))
+ self.play(GrowArrow(arrrow_1), GrowArrow(arrrow_2), Write(arrrow_1_lab), Write(arrrow_2_lab))
+
+ self.play(Write(derivatives[1]))
+ self.play(Write(derivatives[2]))
+
+ derivatives[3].move_to(2*DOWN + 4.5*LEFT).set_color(GREEN_C)
+ derivatives[4].move_to(2*DOWN + 1.5*LEFT).set_color(PINK)
+ derivatives[5].move_to(2*DOWN + 1.5*RIGHT).set_color(PINK)
+ derivatives[6].move_to(2*DOWN + 4.5*RIGHT).set_color(ORANGE)
+
+ arrrow_3 = Arrow(derivatives[1].get_bottom(), derivatives[3].get_top())
+ arrrow_3_lab = partial_derivatives[0].copy().scale(0.7)
+ arrrow_3_lab.move_to(4.3*LEFT+ 0.8*DOWN)
+
+ arrrow_4 = Arrow(derivatives[1].get_bottom(), derivatives[4].get_top())
+ arrrow_4_lab = partial_derivatives[1].copy().scale(0.7)
+ arrrow_4_lab.move_to(1.6*LEFT+ 0.8*DOWN)
+
+ arrrow_5 = Arrow(derivatives[2].get_bottom(), derivatives[5].get_top())
+ arrrow_5_lab = partial_derivatives[0].copy().scale(0.7)
+ arrrow_5_lab.move_to(1.6*RIGHT+ 0.8*DOWN)
+
+ arrrow_6 = Arrow(derivatives[2].get_bottom(), derivatives[6].get_top())
+ arrrow_6_lab = partial_derivatives[1].copy().scale(0.7)
+ arrrow_6_lab.move_to(4.3*RIGHT+ 0.8*DOWN)
+
+ self.play(GrowArrow(arrrow_3), GrowArrow(arrrow_4), Write(arrrow_3_lab), Write(arrrow_4_lab))
+ self.play(Write(derivatives[3]), Write(derivatives[4]))
+
+ self.play(GrowArrow(arrrow_5), GrowArrow(arrrow_6), Write(arrrow_5_lab), Write(arrrow_6_lab))
+ self.play(Write(derivatives[5]), Write(derivatives[6]))
+
+ brace1 = Brace(derivatives[4:6], DOWN, buff = SMALL_BUFF, color = RED_C)
+ brace_t1 = brace1.get_text("Mixed partial derivatives are the same!")
+ brace_t1.set_color(RED_C)
+
+ self.play(GrowFromCenter(brace1), FadeIn(brace_t1))
+
+ self.wait()
+
+
+
diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file7_partial_deriv_clariant_rule.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file7_partial_deriv_clariant_rule.py new file mode 100644 index 0000000..313c6cd --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file7_partial_deriv_clariant_rule.py @@ -0,0 +1,108 @@ +from manimlib.imports import *
+
+class ClariantRule(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ function = ParametricSurface(
+ lambda u, v: np.array([
+ 3.5*np.sin(u)*np.cos(v),
+ 3.5*np.sin(u)*np.sin(v),
+ 3.5*3.5*np.sin(u)*np.sin(u)*(1+2*np.sin(v)*np.sin(v))*np.exp(1 - 3.5*3.5*np.sin(u)*np.sin(u) )
+ ]),u_min=0,u_max=PI,v_min=0,v_max=2*PI, color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.1,
+ resolution=(15, 32)).scale(1)
+
+
+ function_copy1 = function.copy()
+ function_copy2 = function.copy()
+
+ func_x =ParametricFunction(
+ lambda u : np.array([
+ u,
+ -1,
+ (u*u )*np.exp(1-u*u)
+ ]),color=RED_E,t_min=-3.5,t_max=3.5,
+ )
+
+ func_y =ParametricFunction(
+ lambda u : np.array([
+ 0,
+ u,
+ (3*u*u)*np.exp(1-u*u)
+ ]),color=PINK,t_min=-3.5,t_max=3.5,
+ )
+
+ plane_x = Polygon(np.array([-3.5,-1,-3]),np.array([3.5,-1,-3]),np.array([3.5,-1,3]),np.array([-3.5,-1,3]),np.array([-3.5,-1,-3]), color = YELLOW_E, fill_color = YELLOW_B, fill_opacity = 0.1)
+ plane_text_x = TextMobject(r"$y = -1$", color = YELLOW_C).move_to(np.array([5,0,2.7])).scale(0.7)
+
+ plane_y = Polygon(np.array([0,-3.5,-3]),np.array([0,3.5,-3]),np.array([0,3.5,3]),np.array([0,-3.5,3]),np.array([0,-3.5,-3]), color = GREEN_E, fill_color = GREEN_B, fill_opacity = 0.1)
+ plane_text_y = TextMobject(r"$x = 0$", color = GREEN_C).move_to(np.array([0,4,2.7])).scale(0.7)
+
+ surface_eqn = TextMobject("Surface", r"$z = (x^2 + 3y^2)e^{(1 - x^2 - y^2)}$", color = YELLOW_C).scale(0.6).move_to(np.array([4.6*LEFT+3.5*UP]))
+ surface_eqn[0].set_color(BLUE_C)
+
+ self.set_camera_orientation(phi=60 * DEGREES, theta = 45*DEGREES)
+
+ self.add(axes)
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(ShowCreation(function))
+
+ self.add_fixed_in_frame_mobjects(surface_eqn)
+
+ self.play(ShowCreation(plane_x), ShowCreation(plane_y))
+ self.add_fixed_orientation_mobjects(plane_text_x, plane_text_y)
+
+ self.play(ShowCreation(func_x), ShowCreation(func_y))
+
+ dot_x = Dot().rotate(PI/2).set_color(YELLOW_E)
+ alpha_x = ValueTracker(0)
+ vector_x = self.get_tangent_vector(alpha_x.get_value(),func_x,scale=1.5)
+ dot_x.add_updater(lambda m: m.move_to(vector_x.get_center()))
+ self.play(
+ ShowCreation(func_x),
+ GrowFromCenter(dot_x),
+ GrowArrow(vector_x)
+ )
+ vector_x.add_updater(
+ lambda m: m.become(
+ self.get_tangent_vector(alpha_x.get_value()%1,func_x,scale=1.5)
+ )
+ )
+ dot_y = Dot().rotate(PI/2).set_color(GREEN_E)
+ alpha_y = ValueTracker(0)
+ vector_y = self.get_tangent_vector(alpha_y.get_value(),func_y,scale=1.5)
+ dot_y.add_updater(lambda m: m.move_to(vector_y.get_center()))
+ self.play(
+ ShowCreation(func_y),
+ GrowFromCenter(dot_y),
+ GrowArrow(vector_y)
+ )
+ vector_y.add_updater(
+ lambda m: m.become(
+ self.get_tangent_vector(alpha_y.get_value()%1,func_y,scale=1.5)
+ )
+ )
+ self.add(vector_x,dot_x)
+
+ self.play(alpha_x.increment_value, 1, run_time=10, rate_func=linear)
+
+ self.add(vector_y,dot_y)
+ self.play(alpha_y.increment_value, 1, run_time=10, rate_func=linear)
+
+ self.wait(2)
+
+
+
+
+
+
+
+
diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file8_chain_rule.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file8_chain_rule.py new file mode 100644 index 0000000..f50d2d1 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/file8_chain_rule.py @@ -0,0 +1,60 @@ +from manimlib.imports import *
+
+class ChainRule(Scene):
+ def construct(self):
+
+ chain_rule = TextMobject(r"$\frac{dw}{dt}$", r"=", r"$\frac{\partial w}{\partial x}$", r"$\frac{dx}{dt}$", r"+", r"$\frac{\partial w}{\partial y}$", r"$\frac{dy}{dt}$").move_to(4*RIGHT).scale(0.8)
+
+ chain_rule[0].set_color(ORANGE)
+ chain_rule[2].set_color(GREEN_C)
+ chain_rule[3].set_color(RED_C)
+ chain_rule[5].set_color(YELLOW_C)
+ chain_rule[6].set_color(BLUE_C)
+
+ functions = TextMobject(r"$w =f(x,y)$",r"$x$", r"$y$", r"$t$")
+
+ functions[0].move_to(3.3*UP+1*LEFT).set_color(ORANGE)
+ functions[1].move_to(3.3*LEFT).set_color(PURPLE)
+ functions[2].move_to(1.3*RIGHT).set_color(PURPLE)
+ functions[3].move_to(3.3*DOWN+1*LEFT).set_color(WHITE)
+
+ partial_derivatives = TextMobject(r"$\frac{\partial w}{\partial x}$", r"$\frac{\partial w}{\partial y}$")
+
+ partial_derivatives[0].move_to(1.5*UP+3*LEFT).set_color(GREEN_C)
+ partial_derivatives[1].move_to(1.5*UP+1*RIGHT).set_color(YELLOW_C)
+
+ derivatives = TextMobject(r"$\frac{dx}{dt}$", r"$\frac{dy}{dt}$")
+
+ derivatives[0].move_to(1.5*DOWN+3*LEFT).set_color(RED_C)
+ derivatives[1].move_to(1.5*DOWN+1*RIGHT).set_color(BLUE_C)
+
+ line_f_x = Line(np.array([-1,3,0]), np.array([-3,0,0]), color = BLUE_C)
+ line_f_y = Line(np.array([-1,3,0]), np.array([1,0,0]), color = BLUE_C)
+ line_x_t = Line(np.array([-3,0,0]), np.array([-1,-3,0]), color = BLUE_C)
+ line_y_t = Line(np.array([1,0,0]), np.array([-1,-3,0]), color = BLUE_C)
+
+ dot_f = Dot().shift(np.array([-1,3,0])).set_color(BLUE_C)
+ dot_x = Dot().shift(np.array([-3,0,0])).set_color(BLUE_C)
+ dot_y = Dot().shift(np.array([1,0,0])).set_color(BLUE_C)
+ dot_t = Dot().shift(np.array([-1,-3,0])).set_color(BLUE_C)
+
+ variables = TextMobject("Dependent Variable","Intermediate Variables", "Dependent Variable").set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE).scale(0.7)
+ variables[0].move_to(3.3*UP+3.5*RIGHT)
+ variables[1].move_to(3.5*RIGHT)
+ variables[2].move_to(3.3*DOWN+3.5*RIGHT)
+
+ self.play(ShowCreation(dot_f), Write(functions[0]))
+ self.play(ShowCreation(dot_x), ShowCreation(line_f_x), Write(functions[1]), ShowCreation(dot_y), ShowCreation(line_f_y), Write(functions[2]))
+ self.play(Write(partial_derivatives[0]), Write(partial_derivatives[1]))
+ self.wait()
+
+ self.play(ShowCreation(dot_t), ShowCreation(line_x_t), ShowCreation(line_y_t), Write(functions[3]))
+ self.play(Write(derivatives[0]), Write(derivatives[1]))
+ self.wait()
+
+ self.play(Write(variables[0]), Write(variables[1]), Write(variables[2]))
+
+ self.play(FadeOut(variables))
+ self.play(Write(chain_rule))
+ self.wait()
+
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file1_partial_deriv_gas_law.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file1_partial_deriv_gas_law.gif Binary files differnew file mode 100644 index 0000000..8fdb80f --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file1_partial_deriv_gas_law.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file2_partial_deriv_hill.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file2_partial_deriv_hill.gif Binary files differnew file mode 100644 index 0000000..3c758ff --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file2_partial_deriv_hill.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file3_partial_deriv_defn.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file3_partial_deriv_defn.gif Binary files differnew file mode 100644 index 0000000..c66b3fa --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file3_partial_deriv_defn.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file4_partial_deriv_example.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file4_partial_deriv_example.gif Binary files differnew file mode 100644 index 0000000..d2bf541 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file4_partial_deriv_example.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file5_partial_deriv_func_2maximas.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file5_partial_deriv_func_2maximas.gif Binary files differnew file mode 100644 index 0000000..db7f4f8 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file5_partial_deriv_func_2maximas.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file6_clariant_rule.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file6_clariant_rule.gif Binary files differnew file mode 100644 index 0000000..8377827 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file6_clariant_rule.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file7_partial_deriv_clariant_rule.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file7_partial_deriv_clariant_rule.gif Binary files differnew file mode 100644 index 0000000..32d5e92 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file7_partial_deriv_clariant_rule.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file8_chain_rule.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file8_chain_rule.gif Binary files differnew file mode 100644 index 0000000..596b08d --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/partial-derivatives/gifs/file8_chain_rule.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/README.md b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/README.md new file mode 100644 index 0000000..4339c30 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/README.md @@ -0,0 +1,20 @@ +**file1_scalar_function** + + +**file2_domain_range** + + +**file3_parabola_example** + + +**file4_level_curves** + + +**file5_level_surface** + + +**file6_scalar_function_application** + + +**file7_neural_nets** + diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/Scalar_Function_Quiz.pdf b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/Scalar_Function_Quiz.pdf Binary files differindex 6d94a2c..6d94a2c 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/Scalar_Function_Quiz.pdf +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/Scalar_Function_Quiz.pdf diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file1_scalar_functions.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file1_scalar_functions.py new file mode 100644 index 0000000..1a6f4ed --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file1_scalar_functions.py @@ -0,0 +1,50 @@ +from manimlib.imports import *
+
+class ScalarFunction(Scene):
+ def construct(self):
+ circle = Circle(radius = 1.5, color = BLUE_E, fill_color = BLUE_C, fill_opacity = 0.1).move_to(2*LEFT)
+ dot_circle = Dot().shift(np.array([-1.5,0,0])).set_color(BLUE_E)
+ dot_circle_lab = TextMobject(r"$a$", color = BLUE_E).next_to(dot_circle, DOWN)
+
+ arrow = Arrow(np.array([3,-3,0]),np.array([3,3,0]))
+ line = Line(np.array([3,-1.5,0]),np.array([3,1.5,0]), color = RED_C)
+
+ dot0 = Dot().shift(np.array([3,0,0])).set_color(RED_E)
+ dot0_lab = TextMobject(r"$f(a)$", color = RED_E).scale(0.8).next_to(dot0, RIGHT)
+
+ dot1 = Dot().shift(np.array([3,-1.5,0])).set_color(RED_C)
+
+ dot2 = Dot().shift(np.array([3,1.5,0])).set_color(RED_C)
+ dot2_lab = TextMobject(r"$f(A)$", color = RED_C).scale(0.8).next_to(dot2, RIGHT)
+
+ arrow_f = Arrow(np.array([-1.5,0,0]),np.array([3,0,0]), color = YELLOW_C, buff = 0.1)
+
+ R = TextMobject(r"$\mathbb{R}$", color = WHITE).move_to(np.array([3,-3.3,0]))
+
+ A = TextMobject(r"$A$", color = BLUE_E).move_to(np.array([-2.5,-3.3,0]))
+
+ F = TextMobject(r"$f$", color = GREY).move_to(np.array([0,-2.9,0]))
+
+ F_center = TextMobject(r"$f$", color = YELLOW_C).move_to(np.array([0.8,0.5,0]))
+
+ arrow_R_A = Arrow(np.array([-2.3,-3.3,0]),np.array([2.7,-3.3,0]), color = GREY, buff = 0.1)
+
+ scalar_function = TextMobject(r"Scalar Valued Function", r"$f: A \rightarrow \mathbb{R}$", color = PURPLE).move_to(np.array([0,3.5,0]))
+ scalar_function[1].set_color(GREEN_C)
+
+
+
+ self.play(ShowCreation(circle))
+ self.play(ShowCreation(arrow))
+
+
+ self.play(ShowCreation(dot1), ShowCreation(dot2))
+ self.play(ShowCreation(dot_circle))
+ self.play(ShowCreation(dot_circle_lab), ShowCreation(dot2_lab))
+ self.play(ShowCreation(A), ShowCreation(R))
+ self.play(GrowArrow(arrow_f), ShowCreation(dot0), ShowCreation(dot0_lab), ShowCreation(F_center), GrowArrow(arrow_R_A), ShowCreation(F), Transform(circle.copy(), line.copy()))
+
+ self.play(Write(scalar_function))
+
+
+ self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/scalar_function_domain_range.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file2_domain_range.py index 9b1ca7b..1b54cb6 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/scalar_function_domain_range.py +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file2_domain_range.py @@ -20,6 +20,11 @@ class PlotGraphs(GraphScene): self.play(FadeOut(topic))
self.wait(1)
+ scalar_func_R = TextMobject(r"Scalar Valued Functions in $R$").scale(1.5).set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+ self.play(Write(scalar_func_R))
+ self.play(FadeOut(scalar_func_R))
+ self.wait(1)
+
XTD = self.x_axis_width/(self.x_max- self.x_min)
YTD = self.y_axis_height/(self.y_max- self.y_min)
@@ -40,8 +45,8 @@ class PlotGraphs(GraphScene): rangeMsg.scale(0.5)
rangeMsg.set_color(YELLOW)
- domainline1 = Line(self.graph_origin+0.6*YTD*DOWN+1.2*XTD*LEFT, self.graph_origin+0.6*YTD*DOWN + 4*XTD*LEFT)
- domainline2 = Arrow(self.graph_origin+0.6*YTD*DOWN+1.1*XTD*RIGHT, self.graph_origin+0.6*YTD*DOWN + 5.3*XTD*RIGHT)
+ domainline1 = Arrow(self.graph_origin+0.6*YTD*DOWN+1.2*XTD*LEFT, self.graph_origin+0.6*YTD*DOWN + 4*XTD*LEFT, buff = 0.1)
+ domainline2 = Arrow(self.graph_origin+0.6*YTD*DOWN+1.1*XTD*RIGHT, self.graph_origin+0.6*YTD*DOWN + 5.3*XTD*RIGHT, buff = 0.1)
domainline1.set_color(PINK)
domainline2.set_color(PINK)
@@ -128,5 +133,58 @@ class PlotSineGraphs(GraphScene): self.play(Write(domainMsg))
self.wait(3)
+
+
+
+class Paraboloid(ThreeDScene):
+ def construct(self):
+
+ scalar_func_R2 = TextMobject(r"Scalar Valued Functions in $R^2$").scale(1.5).set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+ self.play(Write(scalar_func_R2))
+ self.play(FadeOut(scalar_func_R2))
+ self.wait(1)
+
+ axes = ThreeDAxes()
+
+ paraboloid = ParametricSurface(
+ lambda u, v: np.array([
+ 2*np.sin(u)*np.cos(v),
+ 2*np.sin(u)*np.sin(v),
+ 2*2*np.sin(u)*np.sin(u)
+ ]),u_min=0,u_max=PI/2,v_min=0,v_max=2*PI,checkerboard_colors=[GREEN_C, GREEN_E],
+ resolution=(15, 32)).scale(1)
+
+ domain = Polygon(np.array([-5,-5,0]),np.array([5,-5,0]),np.array([5,5,0]),np.array([-5,5,0]),np.array([-5,-5,0]), color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.2)
+ domain_lab = TextMobject(r"$Domain: R^2$", color = YELLOW_C).scale(0.7).move_to(1*DOWN + 2*LEFT)
+
+ rangef = Line(np.array([0, 0,0]), np.array([0, 0,5]), color = RED_C)
+ rangef_lab = TextMobject(r"$Range: z \geq 0$", color = RED_C).scale(0.7).move_to(2*UP + 1.5*RIGHT)
+
+ func = TextMobject(r"$z = f(x,y) = x^2+y^2$").scale(0.7).move_to(3*UP + 4*LEFT).set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+
+ self.set_camera_orientation(phi=60 * DEGREES, theta = 0*DEGREES)
+ self.begin_ambient_camera_rotation(rate=0.3)
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+
+
+ self.add_fixed_in_frame_mobjects(func)
+ self.play(Write(paraboloid))
+ self.play(ShowCreation(domain))
+ self.add_fixed_in_frame_mobjects(domain_lab)
+ self.wait()
+ self.play(ShowCreation(rangef))
+ self.add_fixed_in_frame_mobjects(rangef_lab)
+ self.wait(5)
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/scalar_function_parabola_example.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file3_parabola_example.py index 74dc063..63c16b3 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/scalar_function_parabola_example.py +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file3_parabola_example.py @@ -9,11 +9,10 @@ class Parabola(ThreeDScene): 2*np.cosh(u)*np.cos(v),
2*np.cosh(u)*np.sin(v),
2*np.sinh(u)
- ]),v_min=0,v_max=TAU,u_min=0,u_max=2,checkerboard_colors=[YELLOW_D, YELLOW_E],
+ ]),v_min=0,v_max=TAU,u_min=0,u_max=2,checkerboard_colors=[YELLOW_D, YELLOW_E],#
resolution=(15, 32))
- text3d = TextMobject(r"Plot of $f: \mathbb{R}^2 \rightarrow \mathbb{R}$", "z = f(x,y)")
- self.add_fixed_in_frame_mobjects(text3d)
+ text3d = TextMobject(r"Plot of $f: \mathbb{R}^2 \rightarrow \mathbb{R}$", r"$z = f(x,y) = \sqrt{x^2 + y^2 - 4}$")
text3d[0].move_to(4*LEFT+2*DOWN)
text3d[1].next_to(text3d[0], DOWN)
text3d[0].set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
@@ -21,8 +20,21 @@ class Parabola(ThreeDScene): #self.set_camera_orientation(phi=0 * DEGREES,theta=270*DEGREES)
self.move_camera(phi=110* DEGREES,theta=45*DEGREES)
+
self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+
self.play(ShowCreation(paraboloid))
+ self.add_fixed_in_frame_mobjects(text3d)
self.play(Write(text3d[0]))
self.play(Write(text3d[1]))
self.begin_ambient_camera_rotation(rate=0.2)
diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file4_level_curves.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file4_level_curves.py new file mode 100644 index 0000000..2b6f719 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file4_level_curves.py @@ -0,0 +1,118 @@ +from manimlib.imports import *
+
+class LevelCurves(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ paraboloid = ParametricSurface(
+ lambda u, v: np.array([
+ u*np.cos(v),
+ u*np.sin(v),
+ -u*u+2
+ ]),u_min=-1.414,u_max=1.414,v_min=0,v_max=2*PI, color = BLUE_C, fill_color = BLUE_C, fill_opacity = 0.1,
+ resolution=(15, 32)).scale(1)
+
+ plane_0 = Polygon(np.array([2,-2,0]),np.array([2,2,0]),np.array([-2,2,0]),np.array([-2,-2,0]),np.array([2,-2,0]), color = BLUE_E, fill_color = BLUE_E, fill_opacity = 0.3)
+ plane_0_lab = TextMobject("C = 0").move_to(0.4*UP+3.2*RIGHT).set_color(BLUE_E).scale(0.6)
+ circle_0 = Circle(radius = 1.414 , color = BLUE_E)
+ circle_0_lab = TextMobject("0").move_to(1.1*DOWN+1.1*RIGHT).set_color(BLUE_E).scale(0.6)
+
+ plane_0_5 = Polygon(np.array([2,-2,0.5]),np.array([2,2,0.5]),np.array([-2,2,0.5]),np.array([-2,-2,0.5]),np.array([2,-2,0.5]), color = GREEN_C, fill_color = GREEN_C, fill_opacity = 0.3)
+ plane_0_5_lab = TextMobject("C = 0.5").move_to(0.8*UP+3.4*RIGHT).set_color(GREEN_C).scale(0.6)
+ circle_0_5 = Circle(radius = 1.224 , color = GREEN_C)
+ circle_0_5_lab = TextMobject("0.5").move_to(0.9*DOWN+0.9*RIGHT).set_color(GREEN_C).scale(0.6)
+ circle_0_5_copy = circle_0_5.copy().move_to(np.array([0,0,0.5]))
+
+ plane_1 = Polygon(np.array([2,-2,1]),np.array([2,2,1]),np.array([-2,2,1]),np.array([-2,-2,1]),np.array([2,-2,1]), color = YELLOW_C, fill_color = YELLOW_C, fill_opacity = 0.3)
+ plane_1_lab = TextMobject("C = 1").move_to(1.2*UP+3.3*RIGHT).set_color(YELLOW_C).scale(0.6)
+ circle_1 = Circle(radius = 1 , color = YELLOW_C)
+ circle_1_lab = TextMobject("1").move_to(0.7*DOWN+0.7*RIGHT).set_color(YELLOW_C).scale(0.6)
+ circle_1_copy = circle_1.copy().move_to(np.array([0,0,1]))
+
+ plane_1_5 = Polygon(np.array([2,-2,1.5]),np.array([2,2,1.5]),np.array([-2,2,1.5]),np.array([-2,-2,1.5]),np.array([2,-2,1.5]), color = ORANGE, fill_color = ORANGE, fill_opacity = 0.3)
+ plane_1_5_lab = TextMobject("C = 1.5").move_to(1.7*UP+3.4*RIGHT).set_color(ORANGE).scale(0.6)
+ circle_1_5 = Circle(radius = 0.707 , color = ORANGE)
+ circle_1_5_lab = TextMobject("1.5").move_to(0.5*DOWN+0.5*RIGHT).set_color(ORANGE).scale(0.6)
+ circle_1_5_copy = circle_1_5.copy().move_to(np.array([0,0,1.5]))
+
+ plane_2 = Polygon(np.array([2,-2,2]),np.array([2,2,2]),np.array([-2,2,2]),np.array([-2,-2,2]),np.array([2,-2,2]), color = RED_C, fill_color = RED_C, fill_opacity = 0.3)
+ plane_2_lab = TextMobject("C = 2").move_to(2.1*UP+3.3*RIGHT).set_color(RED_C).scale(0.6)
+ dot_2 = Dot().set_fill(RED_C)
+ circle_2_lab = TextMobject("2").move_to(0.2*DOWN+0.2*RIGHT).set_color(RED_C).scale(0.6)
+ dot_2_copy = dot_2.copy().move_to(np.array([0,0,2]))
+
+ level_curves_line1 = DashedLine(np.array([0,-1.414,0]),np.array([0,-2,1]), color = WHITE)
+ level_curves_line2 = DashedLine(np.array([0,-1.224,0.5]),np.array([0,-2,1]), color = WHITE)
+ level_curves_line3 = DashedLine(np.array([0,-1,1]),np.array([0,-2,1]), color = WHITE)
+ level_curves_line4 = DashedLine(np.array([0,-0.707,1.5]),np.array([0,-2,1]), color = WHITE)
+ level_curves_line5 = DashedLine(np.array([0,0,2]),np.array([0,-2,1]), color = WHITE)
+
+ level_curves = TextMobject("Level Curves").move_to(1.4*UP+3*LEFT).set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE).scale(0.8)
+
+
+ contour_line1 = DashedLine(np.array([0,-1.414,0]),np.array([0,-2,1]), color = WHITE)
+ contour_line2 = DashedLine(np.array([0,-1.224,0]),np.array([0,-2,1]), color = WHITE)
+ contour_line3 = DashedLine(np.array([0,-1,0]),np.array([0,-2,1]), color = WHITE)
+ contour_line4 = DashedLine(np.array([0,-0.707,0]),np.array([0,-2,1]), color = WHITE)
+ contour_line5 = DashedLine(np.array([0,0,0]),np.array([0,-2,1]), color = WHITE)
+
+ contours = TextMobject("Contours").move_to(1.4*UP+2.7*LEFT).set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE).scale(0.8)
+
+
+ topic = TextMobject("Contour Plot").move_to(3*UP+3*LEFT).set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE).scale(0.8)
+
+ self.set_camera_orientation(phi=80 * DEGREES, theta = 0*DEGREES)
+ #self.set_camera_orientation(phi=0 * DEGREES, theta = 0*DEGREES)
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(Write(paraboloid))
+ self.wait()
+ self.play(ShowCreation(plane_0), ShowCreation(circle_0))
+ self.add_fixed_in_frame_mobjects(plane_0_lab)
+ self.wait()
+ self.play(ShowCreation(plane_0_5), ShowCreation(circle_0_5_copy), ShowCreation(circle_0_5))
+ self.add_fixed_in_frame_mobjects(plane_0_5_lab)
+ self.wait()
+ self.play(ShowCreation(plane_1), ShowCreation(circle_1_copy), ShowCreation(circle_1))
+ self.add_fixed_in_frame_mobjects(plane_1_lab)
+ self.wait()
+ self.play(ShowCreation(plane_1_5), ShowCreation(circle_1_5_copy), ShowCreation(circle_1_5))
+ self.add_fixed_in_frame_mobjects(plane_1_5_lab)
+ self.wait()
+ self.play(ShowCreation(plane_2), ShowCreation(dot_2_copy), ShowCreation(dot_2))
+ self.add_fixed_in_frame_mobjects(plane_2_lab)
+ self.wait()
+
+ self.move_camera(phi=60 * DEGREES, theta = 30*DEGREES,run_time=3)
+ self.play(FadeOut(plane_0), FadeOut(plane_0_lab), FadeOut(plane_0_5), FadeOut(plane_0_5_lab), FadeOut(plane_1), FadeOut(plane_1_lab), FadeOut(plane_1_5), FadeOut(plane_1_5_lab), FadeOut(plane_2), FadeOut(plane_2_lab))
+
+ self.play(GrowArrow(level_curves_line1), GrowArrow(level_curves_line2), GrowArrow(level_curves_line3), GrowArrow(level_curves_line4), GrowArrow(level_curves_line5))
+ self.add_fixed_in_frame_mobjects(level_curves)
+ self.wait()
+ self.play(FadeOut(level_curves_line1), FadeOut(level_curves_line2), FadeOut(level_curves_line3), FadeOut(level_curves_line4), FadeOut(level_curves_line5), FadeOut(level_curves))
+ self.play(FadeOut(circle_0_5_copy), FadeOut(circle_1_copy), FadeOut(circle_1_5_copy), FadeOut(dot_2_copy))
+ self.wait()
+
+ self.play(GrowArrow(contour_line1), GrowArrow(contour_line2), GrowArrow(contour_line3), GrowArrow(contour_line4), GrowArrow(contour_line5))
+ self.add_fixed_in_frame_mobjects(contours)
+ self.wait()
+ self.play(FadeOut(contour_line1), FadeOut(contour_line2), FadeOut(contour_line3), FadeOut(contour_line4), FadeOut(contour_line5), FadeOut(contours))
+
+
+ self.move_camera(phi=0 * DEGREES, theta = 0*DEGREES,run_time=3)
+ self.play(FadeOut(paraboloid))
+ self.wait()
+
+ self.add_fixed_in_frame_mobjects(circle_0_lab, circle_0_5_lab, circle_1_lab, circle_1_5_lab,circle_2_lab)
+ self.add_fixed_in_frame_mobjects(topic)
+ self.wait(3)
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file5_level_surface.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file5_level_surface.py new file mode 100644 index 0000000..8052676 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file5_level_surface.py @@ -0,0 +1,78 @@ +from manimlib.imports import *
+
+class LevelSurface(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+
+ surface_0 = ParametricSurface(
+ lambda u, v: np.array([
+ u*np.cos(v),
+ u*np.sin(v),
+ (u*u*np.cos(v)*np.cos(v))-(u*np.sin(v)/5)+0
+ ]),u_min=-1,u_max=1,v_min=0,v_max=2*PI,checkerboard_colors=[RED_C, RED_E],
+ resolution=(15, 32)).scale(1)
+
+ k_0 = TextMobject("K = 0", color = RED_C).scale(0.7)
+
+ surface_1 = ParametricSurface(
+ lambda u, v: np.array([
+ u*np.cos(v),
+ u*np.sin(v),
+ (u*u*np.cos(v)*np.cos(v))-(u*np.sin(v)/5)+1
+ ]),u_min=-1,u_max=1,v_min=0,v_max=2*PI,checkerboard_colors=[GREEN_C, GREEN_E],
+ resolution=(15, 32)).scale(1)
+
+ k_1 = TextMobject("K = 1", color = GREEN_C).scale(0.7)
+
+ surface_2 = ParametricSurface(
+ lambda u, v: np.array([
+ u*np.cos(v),
+ u*np.sin(v),
+ (u*u*np.cos(v)*np.cos(v))-(u*np.sin(v)/5)+2
+ ]),u_min=-1,u_max=1,v_min=0,v_max=2*PI,checkerboard_colors=[YELLOW_C, YELLOW_E],
+ resolution=(15, 32)).scale(1)
+
+ k_2 = TextMobject("K = 2", color = YELLOW_C).scale(0.7)
+
+ func = TextMobject(r"$w = g(x,y,z)$", r"$= z - f(x,y)$", r"$z-x^2+y/5 = K$")
+ func.set_color_by_gradient(RED, ORANGE, YELLOW, GREEN, BLUE, PURPLE)
+
+ self.set_camera_orientation(phi=90 * DEGREES, theta = 90*DEGREES)
+ self.begin_ambient_camera_rotation(rate=0.3)
+
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(3.7*UP)
+
+ self.add_fixed_in_frame_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
+
+ self.play(Write(surface_0))
+ self.add_fixed_in_frame_mobjects(k_0)
+ k_0.move_to(np.array([1.4*RIGHT ]))
+
+ self.play(Write(surface_1))
+ self.add_fixed_in_frame_mobjects(k_1)
+ k_1.move_to(np.array([1.4*RIGHT + 1*UP]))
+
+ self.play(Write(surface_2))
+ self.add_fixed_in_frame_mobjects(k_2)
+ k_2.move_to(np.array([1.4*RIGHT + 2*UP]))
+ self.wait()
+
+ self.add_fixed_in_frame_mobjects(func)
+ func[0].move_to(np.array([4.5*LEFT + 3*UP]))
+ func[1].move_to(np.array([4.5*LEFT + 2.5*UP]))
+ func[2].move_to(np.array([4.5*LEFT + 2*UP]))
+
+ self.wait(3)
+ self.move_camera(phi=60 * DEGREES,run_time=3)
+ self.wait(2)
+
+
+
\ No newline at end of file diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/scalar_function_application.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file6_scalar_function_application.py index 56b3e53..3ccfad6 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/scalar_function_application.py +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file6_scalar_function_application.py @@ -3,12 +3,23 @@ from manimlib.imports import * class ScalarApplication(ThreeDScene):
def construct(self):
axes = ThreeDAxes() # creates a 3D Axis
+
+ self.add(axes)
+
+ axis = TextMobject(r"X",r"Y",r"Z")
+ axis[0].move_to(6*RIGHT)
+ axis[1].move_to(6*UP)
+ axis[2].move_to(np.array([0,0,3.7]))
+
+ self.add_fixed_orientation_mobjects(axis[2])
+ self.add_fixed_orientation_mobjects(axis[0])
+ self.add_fixed_orientation_mobjects(axis[1])
cube = Cube()
- cube.set_fill(YELLOW_E, opacity = 0.1)
+ cube.set_fill(YELLOW_C, opacity = 0.2)
cube.scale(2)
self.set_camera_orientation(phi=0 * DEGREES,theta=270*DEGREES)
- self.play(ShowCreation(cube),ShowCreation(axes))
+ self.play(ShowCreation(cube))
dot = Sphere()
dot.scale(0.1)
diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/scalar_function_neural_nets.py b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file7_neural_nets.py index eb6bf45..eb6bf45 100644 --- a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/Scalar Functions/scalar_function_neural_nets.py +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/file7_neural_nets.py diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file1_scalar_functions.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file1_scalar_functions.gif Binary files differnew file mode 100644 index 0000000..bea9c7b --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file1_scalar_functions.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file2_domain_range.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file2_domain_range.gif Binary files differnew file mode 100644 index 0000000..6801e4f --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file2_domain_range.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file3_parabola_example.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file3_parabola_example.gif Binary files differnew file mode 100644 index 0000000..9576b4a --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file3_parabola_example.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file4_level_curves.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file4_level_curves.gif Binary files differnew file mode 100644 index 0000000..b4ac106 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file4_level_curves.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file5_level_surface.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file5_level_surface.gif Binary files differnew file mode 100644 index 0000000..e4dc80d --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file5_level_surface.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file6_scalar_function_application.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file6_scalar_function_application.gif Binary files differnew file mode 100644 index 0000000..8bb176a --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file6_scalar_function_application.gif diff --git a/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file7_neural_nets.gif b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file7_neural_nets.gif Binary files differnew file mode 100644 index 0000000..a22f1b8 --- /dev/null +++ b/FSF-2020/calculus-of-several-variables/multivariable-functions-and-paritial-derivatives/scalar-functions/gifs/file7_neural_nets.gif diff --git a/FSF-2020/calculus/intro-to-calculus/README.md b/FSF-2020/calculus/intro-to-calculus/README.md index e69de29..a417361 100644 --- a/FSF-2020/calculus/intro-to-calculus/README.md +++ b/FSF-2020/calculus/intro-to-calculus/README.md @@ -0,0 +1,8 @@ +Contributor: Aryan Singh
+Subtopics covered
+ - When do limits exist?
+ - How Fast am I going?-An intro to derivatives
+ - Infinte sums in a nutshell(Riemann integrals)
+ - Fundamental Theorem of calculus
+ - Volume and surface area of Gabriel's Horn
+ - Infinite sequences and series
diff --git a/FSF-2020/calculus/intro-to-calculus/introderivative/derivative1.py b/FSF-2020/calculus/intro-to-calculus/introderivative/derivative1.py new file mode 100644 index 0000000..79a6fc6 --- /dev/null +++ b/FSF-2020/calculus/intro-to-calculus/introderivative/derivative1.py @@ -0,0 +1,55 @@ +from manimlib.imports import * +class derivative1(GraphScene, Scene): + def setup(self): + GraphScene.setup(self) + CONFIG = { + "y_max" : 4, + "y_min" : -2, + "x_max" : 4, + "x_min" : -2, + "y_tick_frequency" : 1, + "x_tick_frequency" : 1, + "axes_color" : WHITE, + "num_graph_anchor_points": 3000, #this is the number of points that graph manim + "graph_origin" : ORIGIN+2*DOWN+4*LEFT, + "x_labeled_nums": list(range(-2,5)), + "y_labeled_nums": list(range(-2,5)), + "x_axis_label":"$x$", + "y_axis_label":r"$f(x)=y= 3-\frac { 3 }{ 2 } x$", + "x_axis_width": 5, + "y_axis_height": 5, + } + def construct(self): + #XTD = self.x_axis_width/(self.x_max - self.x_min) + #YTD = self.y_axis_height/(self.y_max - self.y_min) + + text1 = TextMobject("") + text2 = TexMobject("{y}_{2}-{y}_{1}") + text2 = TexMobject("{x}_{2}-{x}_{1}") + text3 = TexMobject(r"m\quad =\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } }").move_to(np.array([3,0,0])) + text4 = TexMobject(r"m\quad =\frac { 3 }{ -2 }").move_to(np.array([3,0,0])) + text5 = TexMobject(r"m\quad =\quad -1.5").move_to(np.array([3,0,0])) + self.setup_axes() + graph_1 = self.get_graph(lambda x : 3-1.5*x, color = GREEN_SCREEN, x_min = -1, x_max = 3) + graph_2 = self.get_graph(lambda x : 3.1-1.5*x, color = ORANGE, x_min = 0, x_max = 2) + dot1 = Dot() + dot2 = SmallDot(self.graph_origin+1.7*RIGHT, color = PINK) + dot3 = SmallDot(self.graph_origin+2.5*UP, color = RED_B) + vec1 = Vector(2.5*DOWN, color = PINK).shift(self.graph_origin+2.5*UP) + vec2 = Vector(1.7*RIGHT, color = RED_B).shift(self.graph_origin) + brace1 = Brace(vec1, LEFT) + brace2 = Brace(vec2, DOWN) + br1text = brace1.get_text(r"${y}_{2}-{y}_{1}$").next_to(brace1, LEFT) + br2text = brace2.get_text(r"${x}_{2}-{x}_{1}$").next_to(brace2, DOWN) + self.play(ShowCreation(graph_1), ShowCreation(dot2), ShowCreation(dot3)) + self.play(MoveAlongPath(dot1, graph_2), ShowCreation(vec1), ShowCreation(vec2), run_time = 3) + self.wait(1) + self.play(ShowCreation(brace1), ShowCreation(brace2)) + self.play(ShowCreation(br1text), ShowCreation(br2text)) + self.wait(2) + self.play(GrowFromCenter(text3)) + self.wait(2.5) + self.play(ReplacementTransform(text3, text4)) + self.wait(2) + self.play(ReplacementTransform(text4, text5)) + self.wait(2) diff --git a/FSF-2020/calculus/intro-to-calculus/limit/limit1.py b/FSF-2020/calculus/intro-to-calculus/limit/limit1.py new file mode 100644 index 0000000..fe5cb1e --- /dev/null +++ b/FSF-2020/calculus/intro-to-calculus/limit/limit1.py @@ -0,0 +1,105 @@ +from manimlib.imports import * +class limit1(GraphScene,MovingCameraScene): + def setup(self): + GraphScene.setup(self) + MovingCameraScene.setup(self) + CONFIG = { + "y_max" : 1, + "y_min" : 0, + "x_max" : 1, + "x_min" : -1, + "y_tick_frequency" : 0.2, + "x_tick_frequency" : 0.2, + "axes_color" : WHITE, + "num_graph_anchor_points": 3000, #this is the number of points that graph manim + "graph_origin" : ORIGIN+3*DOWN, + "x_labeled_nums": list(range(-1,2)), + "y_labeled_nums": list(range(0,2)), + "x_axis_label":"$x$", + "y_axis_label":"$f(x)$", + "x_axis_width": 10, + "y_axis_height": 5, + } + def construct(self): + XTD = self.x_axis_width/(self.x_max - self.x_min) + YTD = self.y_axis_height/(self.y_max - self.y_min) + + dot1 = SmallDot(np.array([0.025,-2.975,0])) + dot2 = SmallDot(np.array([-0.025,-2.975,0])) + sqr = Square(side_length = 15.0).move_to(np.array([0,-3,0])) + brline1 = DashedVMobject(Line(np.array([0.15,-3,0]), np.array([0.15,-2.85,0]))) + brline2 = DashedVMobject(Line(np.array([0.025,-3,0]), np.array([0.025,-2.975,0]))) + brline3 = DashedVMobject(Line(np.array([-0.15,-3,0]), np.array([-0.15,-2.85,0]))) + brline4 = DashedVMobject(Line(np.array([-0.025,-3,0]), np.array([-0.025,-2.975,0]))) + textdef = TextMobject("") + text003 = TextMobject("0.03").move_to(np.array([0.15,-3.05,0])).scale(0.1) + textazero1 = TexMobject(r"\approx 0").move_to(np.array([0.04,-3.05,0])).scale(0.1) + textazero2 = TexMobject(r"\approx 0").move_to(np.array([-0.04,-3.05,0])).scale(0.1) + textm003 = TextMobject("-0.03").move_to(np.array([-0.15,-3.05,0])).scale(0.1) + text2 = TextMobject("Let f(x) = |x|. We'll check neighbourhood of origin") + text3 = TextMobject("h has to be a very small number greater than 0").move_to(np.array([0,-3.3,0])).scale(0.2) + text4 = TextMobject("The point travels through range of neighbourhood").move_to(np.array([0,-3.3,0])).scale(0.19) + text5 = TextMobject("let h be equal to 0.03").move_to(np.array([0,-3.3,0])).scale(0.25) + text6 = TextMobject("Notice how the point never touches the origin").move_to(np.array([0,-3.3,0])).scale(0.2) + text7 = TextMobject("Green line shows the Right hand neighbourhood of origin").move_to(np.array([0,-3.3,0])).scale(0.17) + text8 = TextMobject("The point is approaching (0,0) for the values of x which are positive").move_to(np.array([0,-3.3,0])).scale(0.1) + text9 = TextMobject("Values of x are tending to 0 from positive side").move_to(np.array([0,-3.3,0])).scale(0.19) + text10 = TexMobject(r"\text {Notation for this is }",r"x\rightarrow { 0 }^{ + }").move_to(np.array([0,-3.3,0])).scale(0.25) + text11 = TextMobject("Similar case can be made for negative values of x").move_to(np.array([0,-3.3,0])).scale(0.19) + text12 = TextMobject("The point is approaching (0,0) for the values of x which are negative").move_to(np.array([0,-3.3,0])).scale(0.1) + text13 = TextMobject("Values of x are tending to 0 from negative side").move_to(np.array([0,-3.3,0])).scale(0.19) + text14 = TexMobject(r"\text {Notation for this is }",r"x\rightarrow { 0 }^{ - }").move_to(np.array([0,-3.3,0])).scale(0.25) + + + self.play(FadeIn(text2), run_time = 1.5) + self.wait(2.5) + self.setup_axes() + graph_1 = self.get_graph(lambda x : x, color = RED, x_min = 0, x_max = 1) + graph_2 = self.get_graph(lambda x : -x, color = RED, x_min = 0, x_max = -1) + graph_3 = self.get_graph(lambda x : x,color = RED, x_min = 0.005, x_max = 0.03) + graph_4 = self.get_graph(lambda x : x,color = GREEN_SCREEN, x_min = 0.03, x_max = 0.005) + graph_5 = self.get_graph(lambda x : -x,color = GREEN_SCREEN, x_min = -0.03, x_max = -0.005) + grp1 = VGroup(graph_1,graph_2) + grp2 = VGroup(brline2, textazero1) + grp3 = VGroup(textazero2, textm003, brline3, brline4) + self.play(ShowCreation(grp1)) + self.add(sqr) + self.play(ReplacementTransform(text2, text3)) + self.camera_frame.save_state() + self.play(self.camera_frame.set_width,2.25,self.camera_frame.move_to,sqr,run_time = 2) + self.wait(2.5) + self.play(ReplacementTransform(text3, text4), ShowCreation(dot1)) + self.wait(2.5) + self.play(ReplacementTransform(text4, text5), ShowCreation(brline1), ShowCreation(text003)) + self.wait(2.5) + for i in range(0,3): + self.play(MoveAlongPath(dot1,graph_3), run_time = 0.5) + self.play(MoveAlongPath(dot1,graph_4), run_time = 0.5) + self.play(ReplacementTransform(text5, text6), ShowCreation(grp2)) + self.wait(2) + self.play(FadeOut(dot1)) + self.add(graph_4) + self.play(ReplacementTransform(text6, text7)) + self.wait(2.5) + self.play(ReplacementTransform(text7,text8)) + for i in range(0,3): + self.play(MoveAlongPath(dot1,graph_4), run_time = 0.7) + self.play(ReplacementTransform(text8, text9)) + self.wait(2.5) + self.play(ReplacementTransform(text9, text10)) + self.wait(2.5) + self.play(ShowCreation(grp3), ReplacementTransform(text10, text11), FadeOut(dot1)) + self.add(graph_5) + for i in range(0,3): + self.play(MoveAlongPath(dot2, graph_5), run_time = 0.7) + self.play(ReplacementTransform(text11, text12)) + self.wait(2.5) + self.play(ReplacementTransform(text12, text13)) + self.wait(2.5) + self.play(ReplacementTransform(text13, text14)) + self.wait(2) + self.play(FadeOut(dot2), ReplacementTransform(text14, textdef)) + self.wait(2) + self.play(Restore(self.camera_frame)) + + self.wait(2.5) diff --git a/FSF-2020/calculus/intro-to-calculus/limit/limit3.py b/FSF-2020/calculus/intro-to-calculus/limit/limit3.py new file mode 100644 index 0000000..a4f07d7 --- /dev/null +++ b/FSF-2020/calculus/intro-to-calculus/limit/limit3.py @@ -0,0 +1,95 @@ +from manimlib.imports import * +class limit3(GraphScene, MovingCameraScene): + def setup(self): + GraphScene.setup(self) + MovingCameraScene.setup(self) + CONFIG = { + "y_max" : 10, + "y_min" : 0, + "x_max" : 100, + "x_min" : 0, + "y_tick_frequency" : 1, + "x_tick_frequency" : 10, + "axes_color" : WHITE, + "num_graph_anchor_points": 3000, #this is the number of points that graph manim + "graph_origin" : ORIGIN+3*DOWN+4*LEFT, + "x_labeled_nums": list(range(0,101))[::10], + "y_labeled_nums": list(range(0,11)), + "x_axis_label":"$x$", + "y_axis_label":"$f(x)$", + "x_axis_width": 10, + "y_axis_height": 5, + } + def construct(self): + XTD = self.x_axis_width/(self.x_max - self.x_min) + YTD = self.y_axis_height/(self.y_max - self.y_min) + sqr1 = Square(side_length = 15).move_to(np.array([1,0.5,0])) + sqr2 = Square(side_length = 15).move_to(np.array([-4,-3,0])) + + textdef = TextMobject("") + text20 = TextMobject("f(x) is not defined at x=50").move_to(np.array([1,0.3,0])).scale(0.2) + text21 = TexMobject(r"\text {f(x) is not defined in interval }",r" (-\infty ,\quad 1]").move_to(np.array([-4,-3.2,0])).scale(0.18) + text22 = TextMobject("1").move_to(np.array([-3.9,-3.05,0])).scale(0.2) + text1 = TexMobject(r"\text {Let }" ,r"f\left( x \right) =\begin{cases} \sqrt { x-1 } ,x\in \quad (1,\infty )-50 \end{cases}") + text2 = TextMobject("Graph of f(x) is ") + text3 = TextMobject("Right hand neighbour of 50 will approximately be 50.000001").move_to(np.array([1,0.3,0])).scale(0.15) + text4 = TextMobject("Left hand neighbour of 50 will approximately be 49.999999").move_to(np.array([1,0.3,0])).scale(0.15) + text5 = TexMobject(r"\text {Hence R.H.L }", r"=\lim _{ x\rightarrow { 50 }^{ + } }{ \sqrt { 50.000001 - 1 } } \approx 7.000000071").move_to(np.array([1,0.3,0])).scale(0.13) + text6 = TexMobject(r"\text{Hence L.H.L }", r" = \lim _{ x\rightarrow { 50 }^{ - } }{ \sqrt { 49.999999-1 } }\approx 6.999999929").move_to(np.array([1,0.3,0])).scale(0.13) + text7 = TextMobject("7.000000071").move_to(np.array([1.9,0.25,0])).scale(0.1) + text8 = TextMobject("6.999999929").move_to(np.array([0.1,0.25,0])).scale(0.1) + text9 = TexMobject(r"6.999999929\quad \approx \quad 7.000000071 \quad \approx 7").move_to(np.array([1,0.25,0])).scale(0.2) + text10 = TexMobject(r"\text{Because LHL }" ,r"\approx" ,r"\text{ RHL, Limit exists at x=50 and equals 7").move_to(np.array([1,0.25,0])).scale(0.13) + text11 = TextMobject("There is no Left hand neighbour of x=1").move_to(np.array([-4,-3.2,0])).scale(0.22) + text12 = TexMobject(r"\therefore\quad \lim _{ x\rightarrow 0 }{ f(x) } \quad =\quad \lim _{ x\rightarrow { 0 }^{ + } }{ f(x) } ").move_to(np.array([-4,-3.2,0])).scale(0.25) + text13 = TexMobject(r"\text {R.H.L =}",r" \lim _{ x\rightarrow { 0 }^{ + } }{ \sqrt { 1.000000000001-1 } } \quad \approx 0").move_to(np.array([-4,-3.2,0])).scale(0.13) + text14 = TexMobject(r"\therefore \quad \lim _{ x\rightarrow 0 }{ f(x)\quad =\quad 0 }").move_to(np.array([-4,-3.2,0])).scale(0.13) + self.camera_frame.save_state() + self.play(ShowCreation(text1)) + self.wait(3) + self.play(ReplacementTransform(text1, text2)) + self.wait() + self.play(ReplacementTransform(text2, textdef)) + self.setup_axes() + self.setup() + graph_1 = self.get_graph(lambda x : (x-1)**(1/2),color = PINK, x_min = 1, x_max = 49.9) + graph_2 = self.get_graph(lambda x : (x-1)**(1/2),color = PINK, x_min = 50.1, x_max = 100) + graph_3 = self.get_graph(lambda x : (x-1)**(1/2),color = PINK, x_min = 1.05, x_max = 1.001) + dot1 = SmallDot(color = PURPLE_A) + cir = Circle(radius = 0.01, color = GREEN_SCREEN).move_to(np.array([1,0.5,0])) + grp1 = VGroup(graph_1, graph_2, cir) + grp2 = VGroup(text7, text8) + self.play(ShowCreation(grp1)) + self.wait(2) + self.play(self.camera_frame.set_width,2.25,self.camera_frame.move_to,sqr1,run_time = 2) + self.wait(1) + self.play(ShowCreation(text20)) + self.wait(2) + self.play(ReplacementTransform(text20, text3)) + self.wait(3) + self.play(ReplacementTransform(text3, text5)) + self.wait(3) + self.play(ReplacementTransform(text5, text7), ShowCreation(text4)) + self.wait(4) + self.play(ReplacementTransform(text4, text6)) + self.wait(3) + self.play(ReplacementTransform(text6, text8)) + self.wait(1.5) + self.play(ReplacementTransform(grp2, text9)) + self.wait(1.5) + self.play(ReplacementTransform(text9, text10)) + self.wait(3) + self.play(self.camera_frame.set_width,2.25,self.camera_frame.move_to,sqr2,run_time = 2) + self.play(ShowCreation(text21), ShowCreation(text22)) + self.play(MoveAlongPath(dot1, graph_3), run_time = 3) + self.wait(3) + self.play(ReplacementTransform(text21, text11)) + self.wait(3) + self.play(ReplacementTransform(text11, text12)) + self.wait(3) + self.play(ReplacementTransform(text12, text13)) + self.wait(2) + self.play(ReplacementTransform(text13, text14)) + self.wait(3) + self.play(ReplacementTransform(text14, textdef)) + self.wait(2) diff --git a/FSF-2020/calculus/intro-to-calculus/riemannintegrals/README.md b/FSF-2020/calculus/intro-to-calculus/riemannintegrals/README.md new file mode 100644 index 0000000..a9ad0bb --- /dev/null +++ b/FSF-2020/calculus/intro-to-calculus/riemannintegrals/README.md @@ -0,0 +1,18 @@ +rierect1.gif +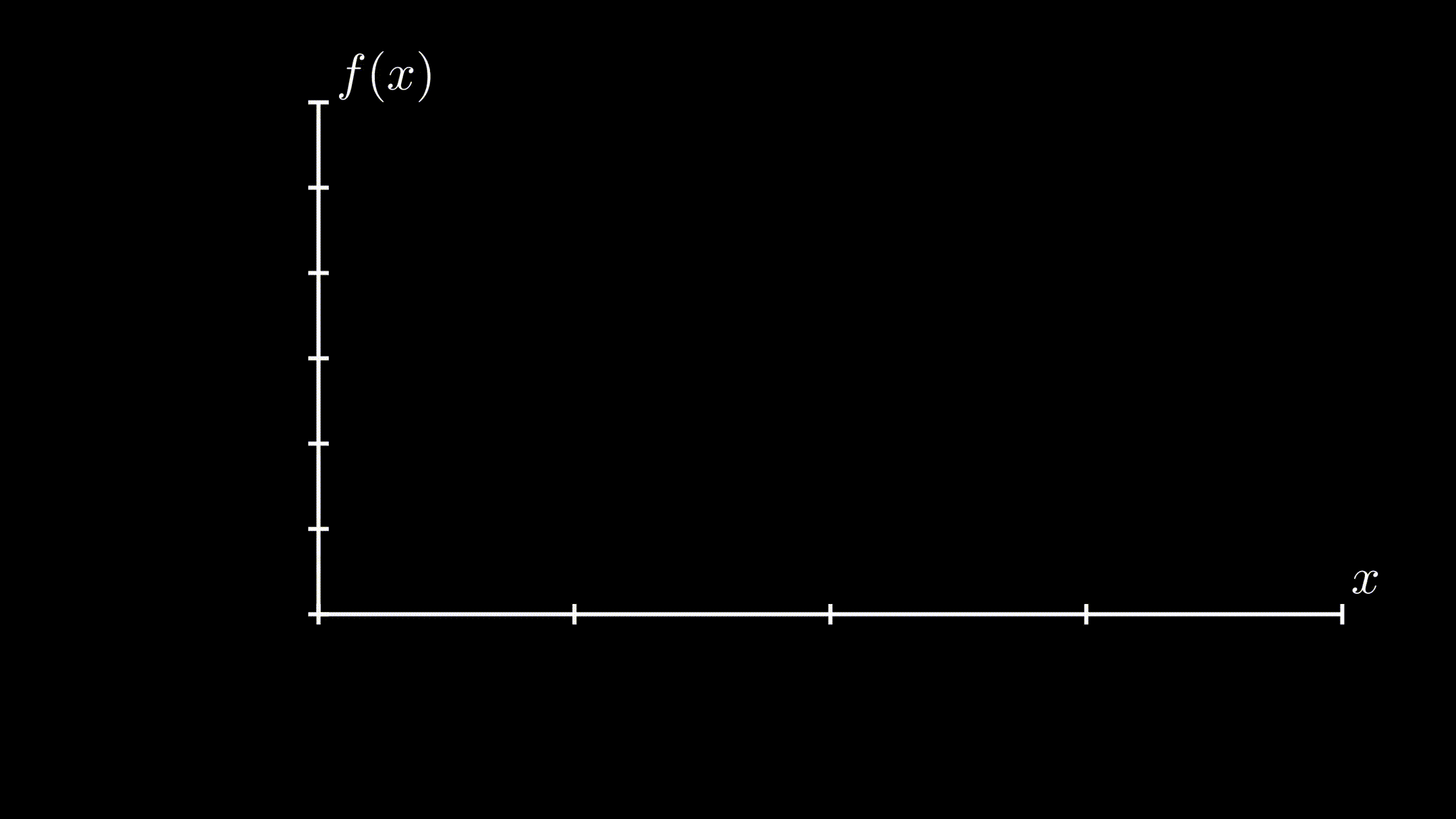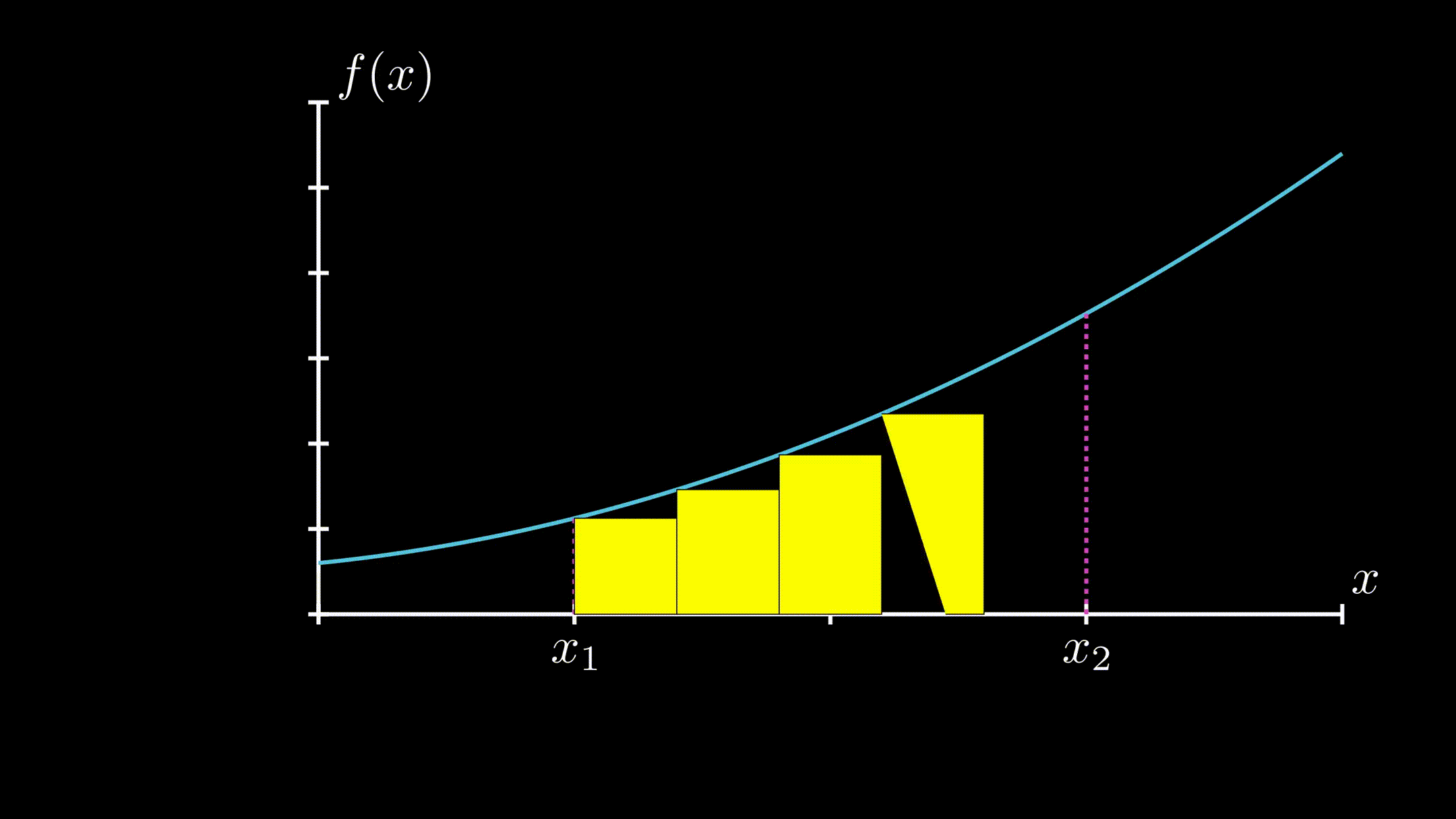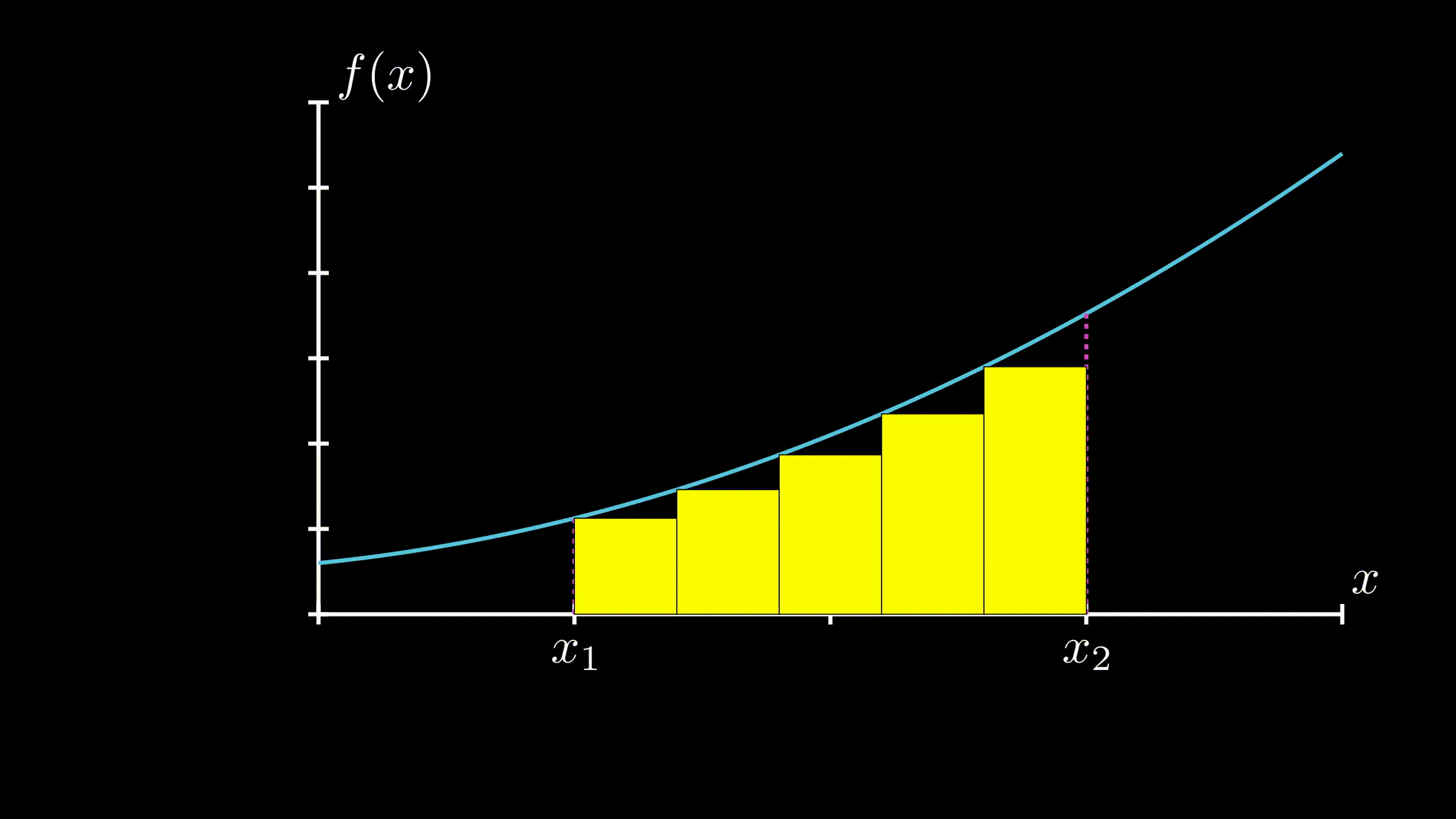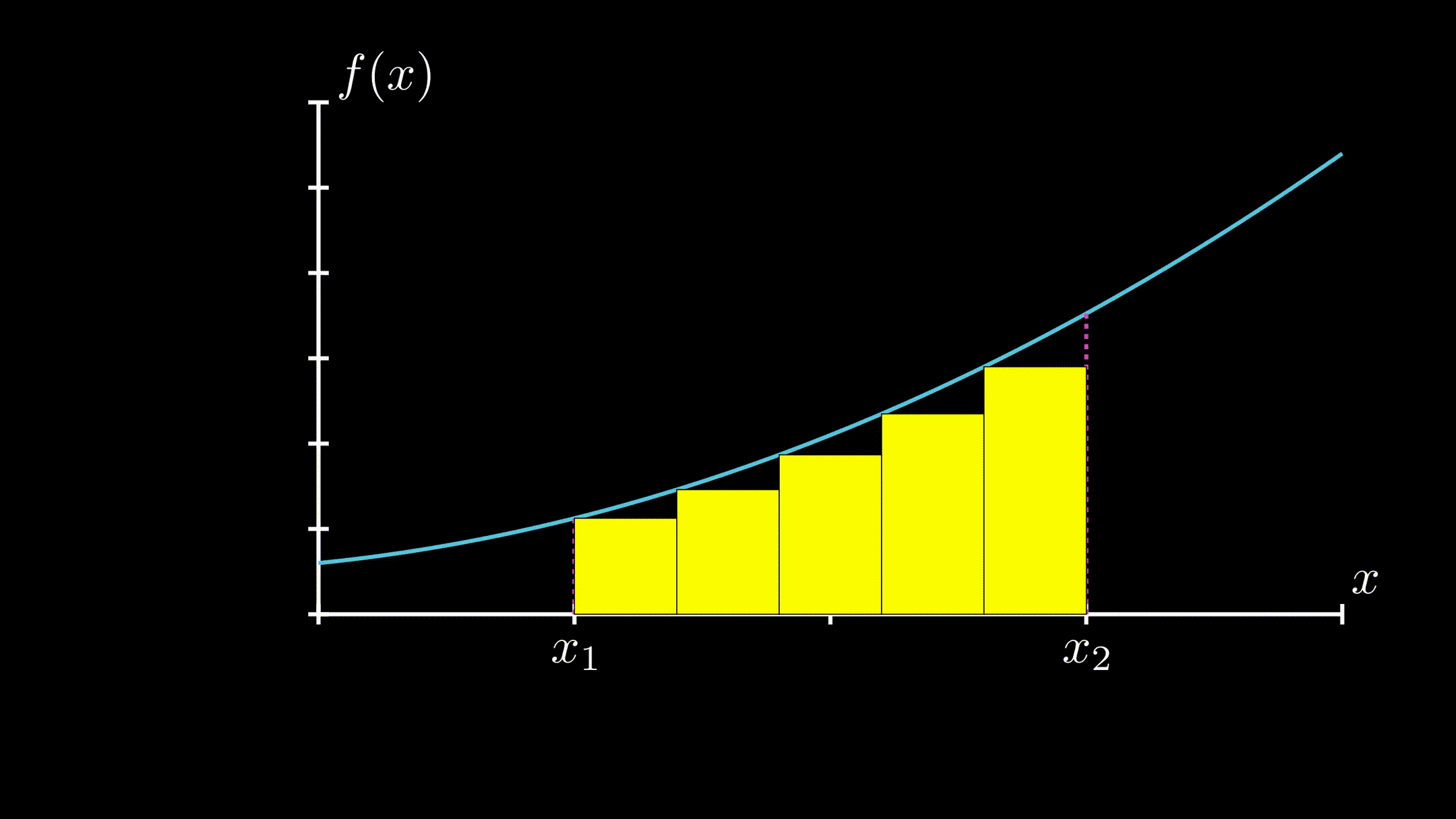 + + +rierect2.gif +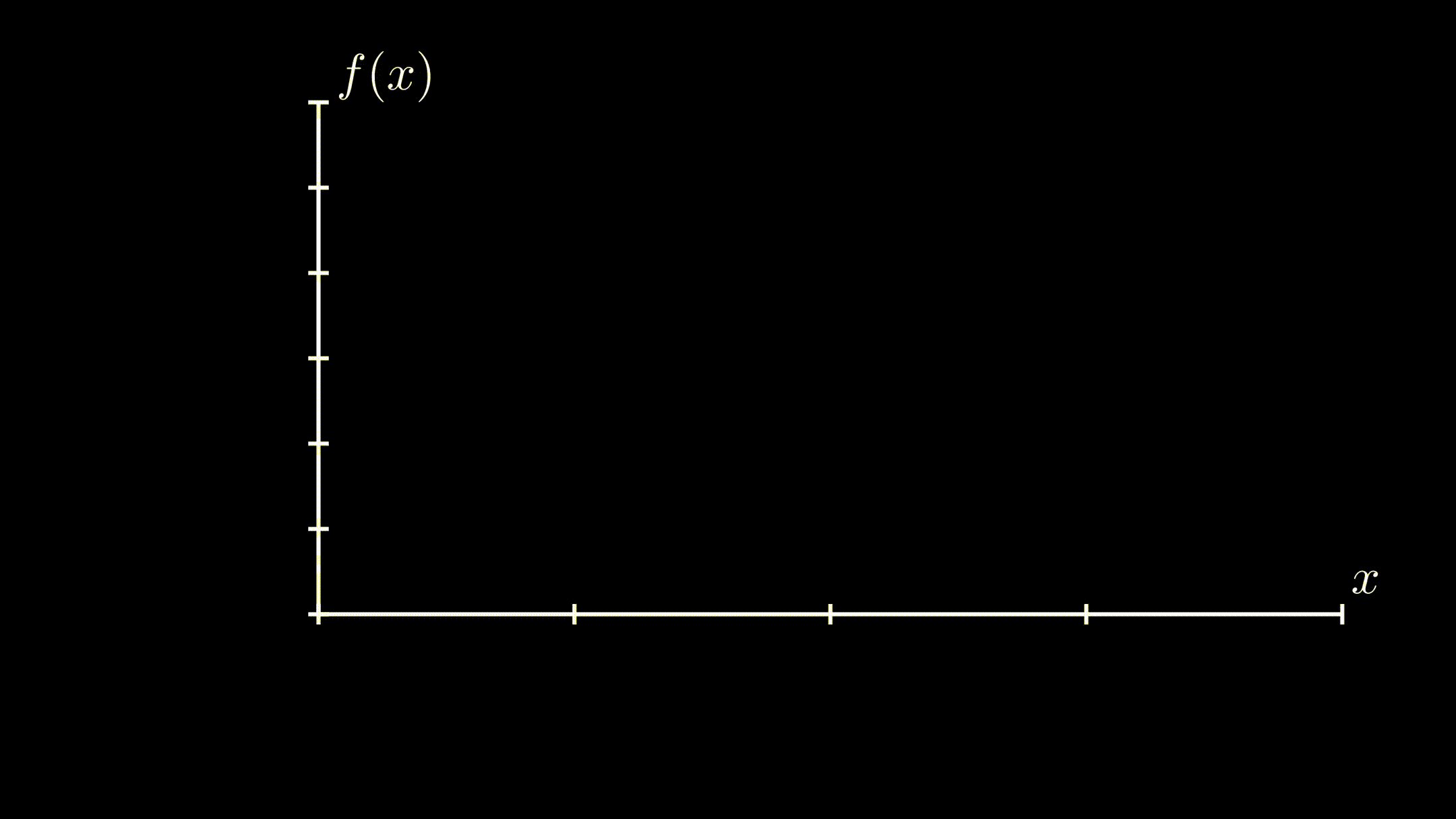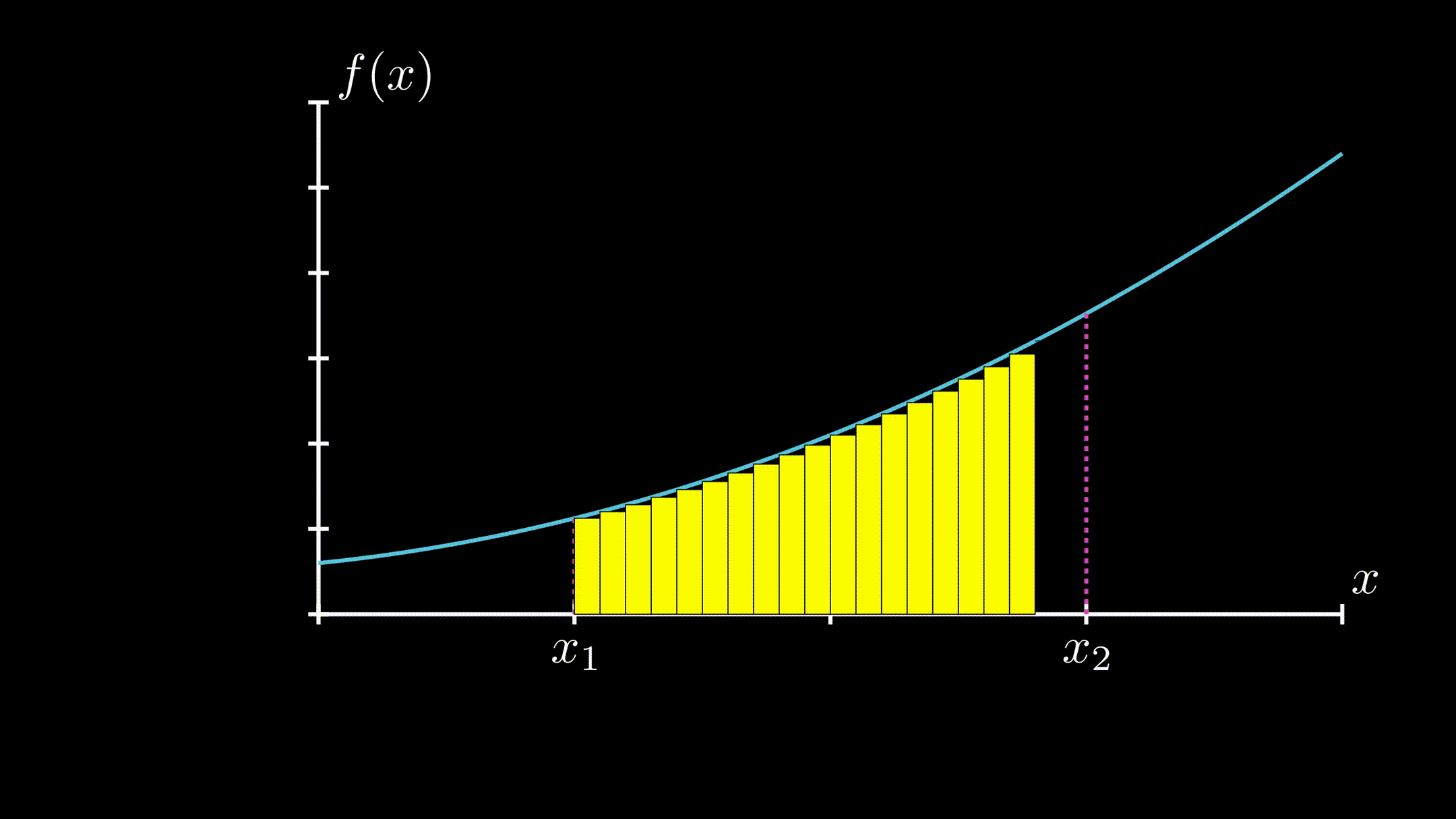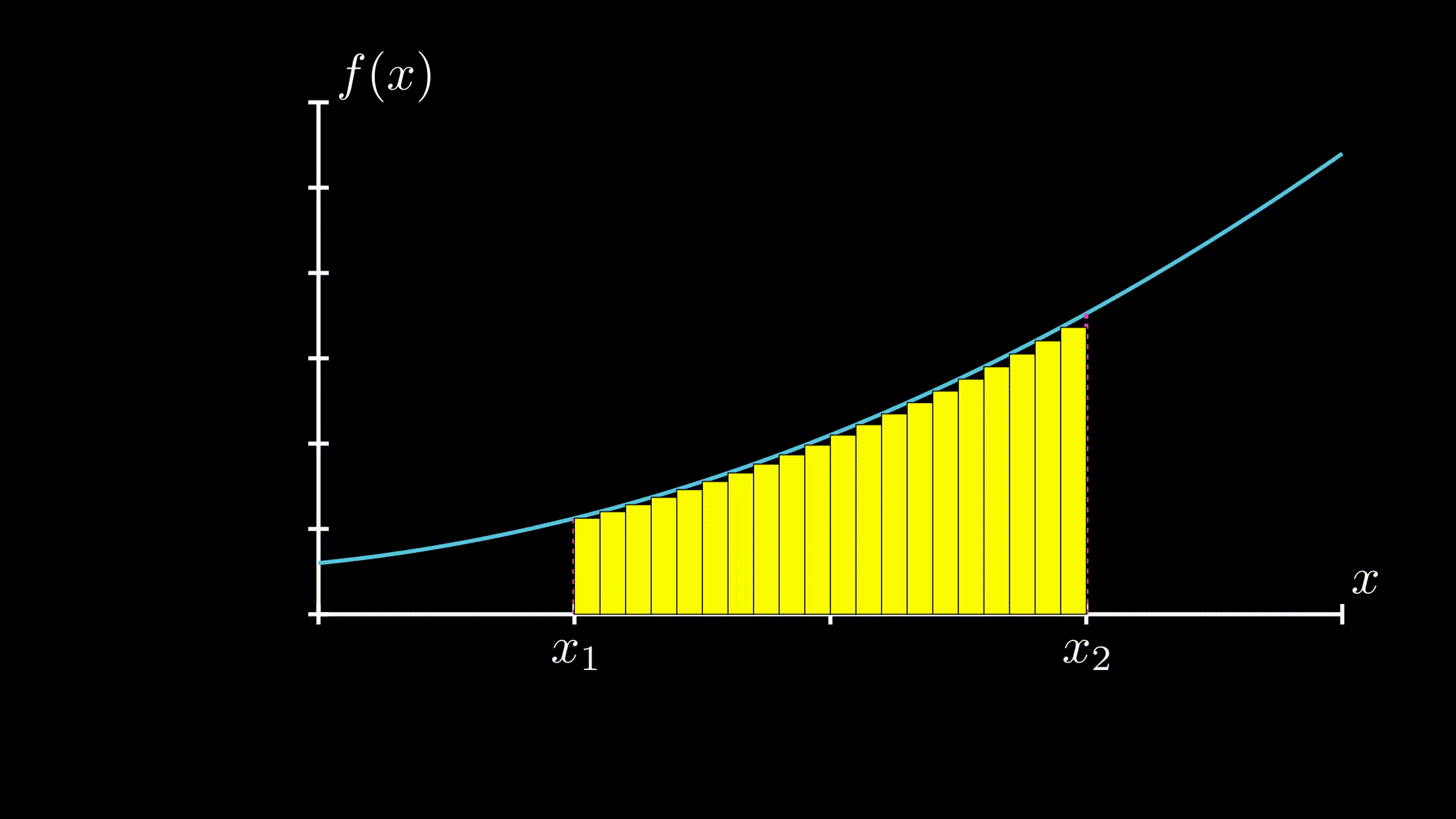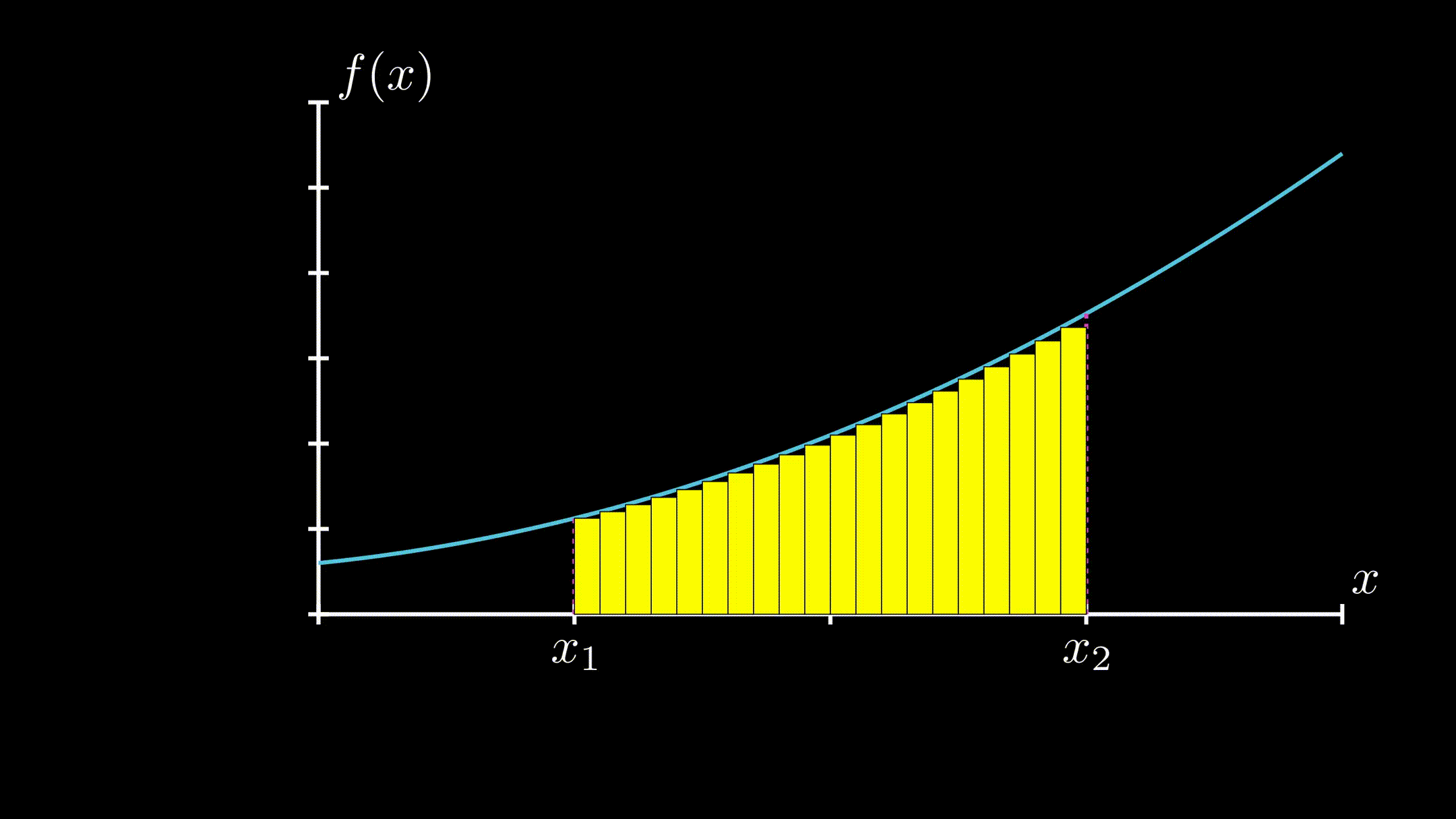 + + +rierect3.gif +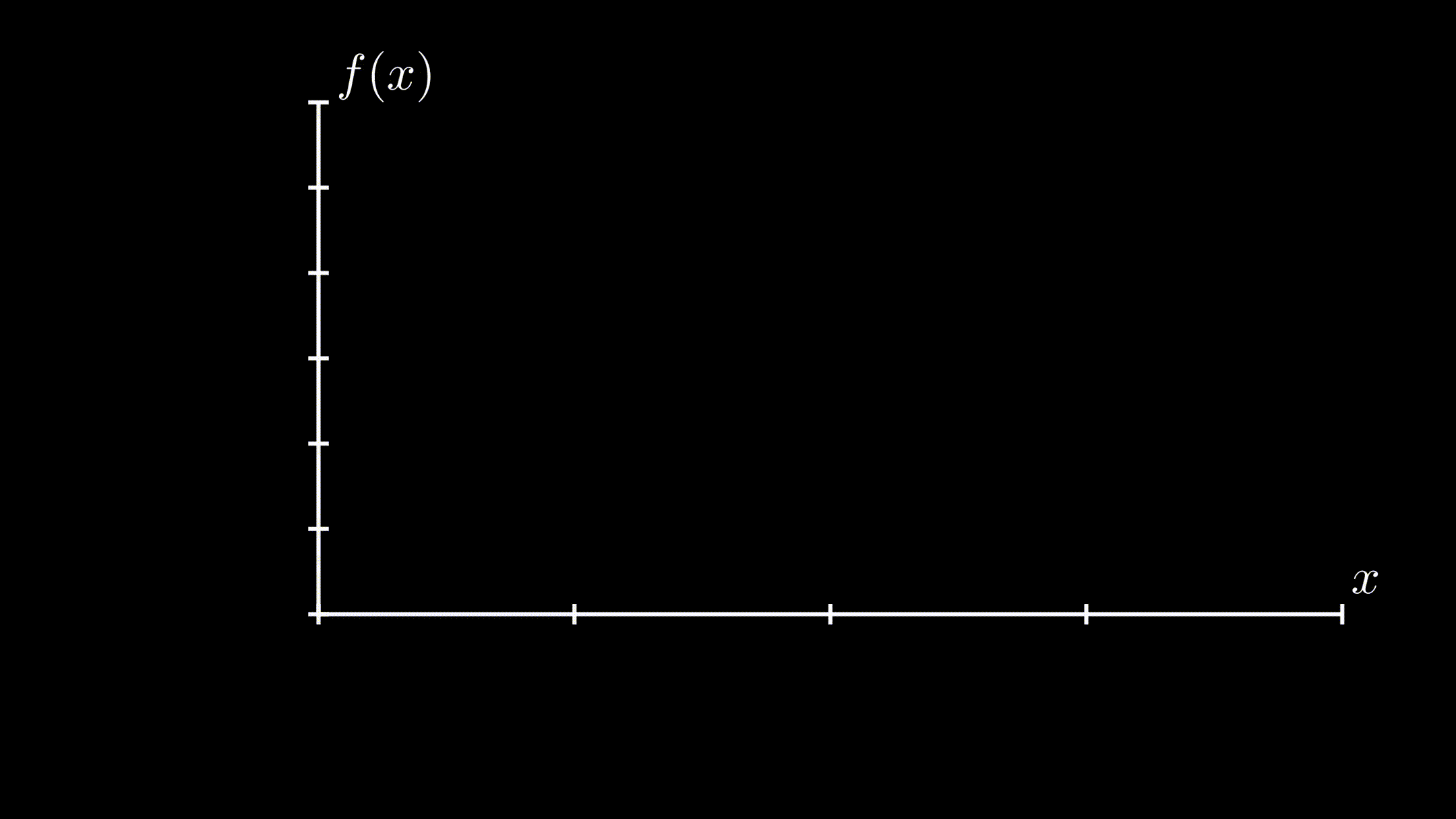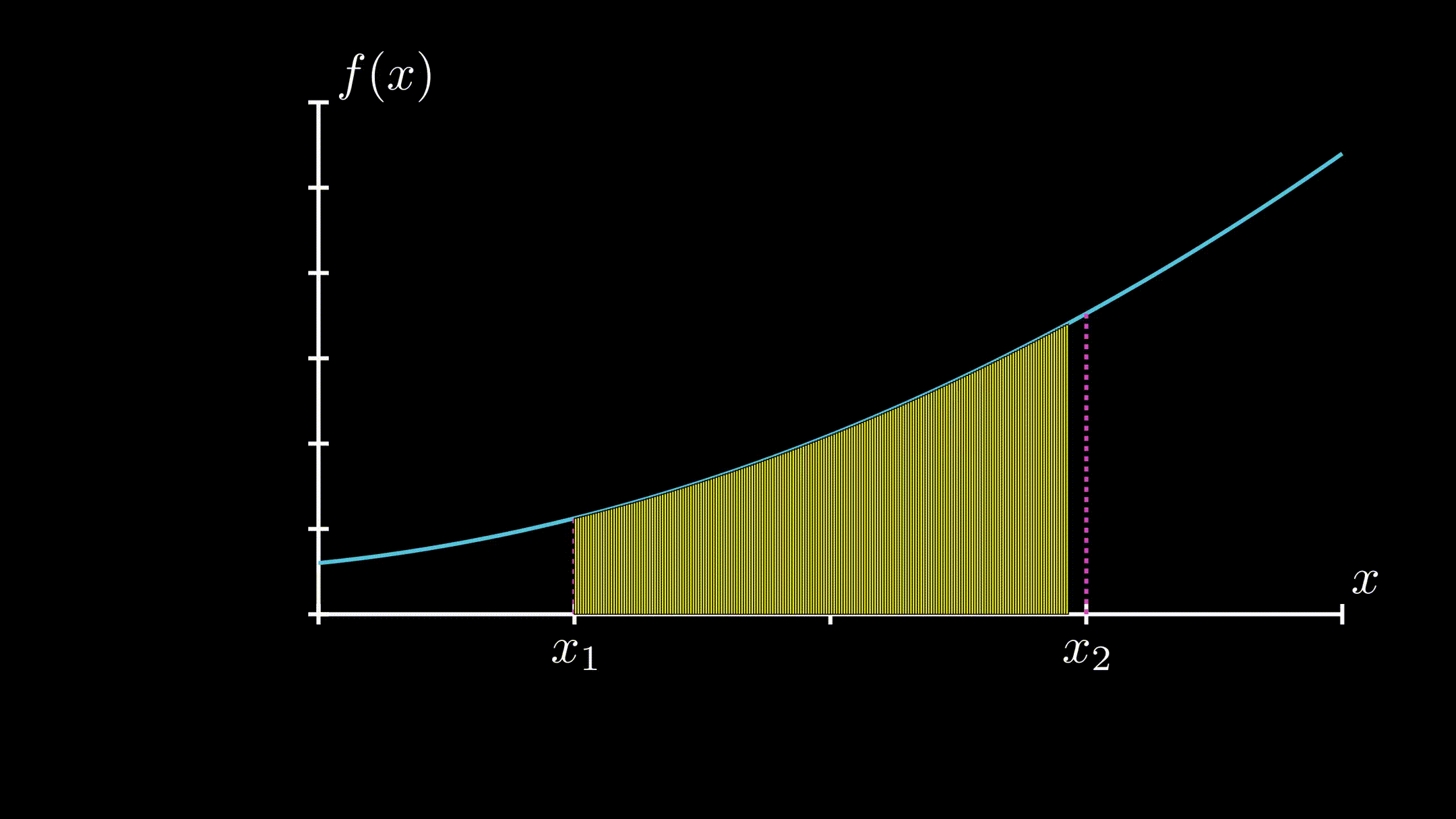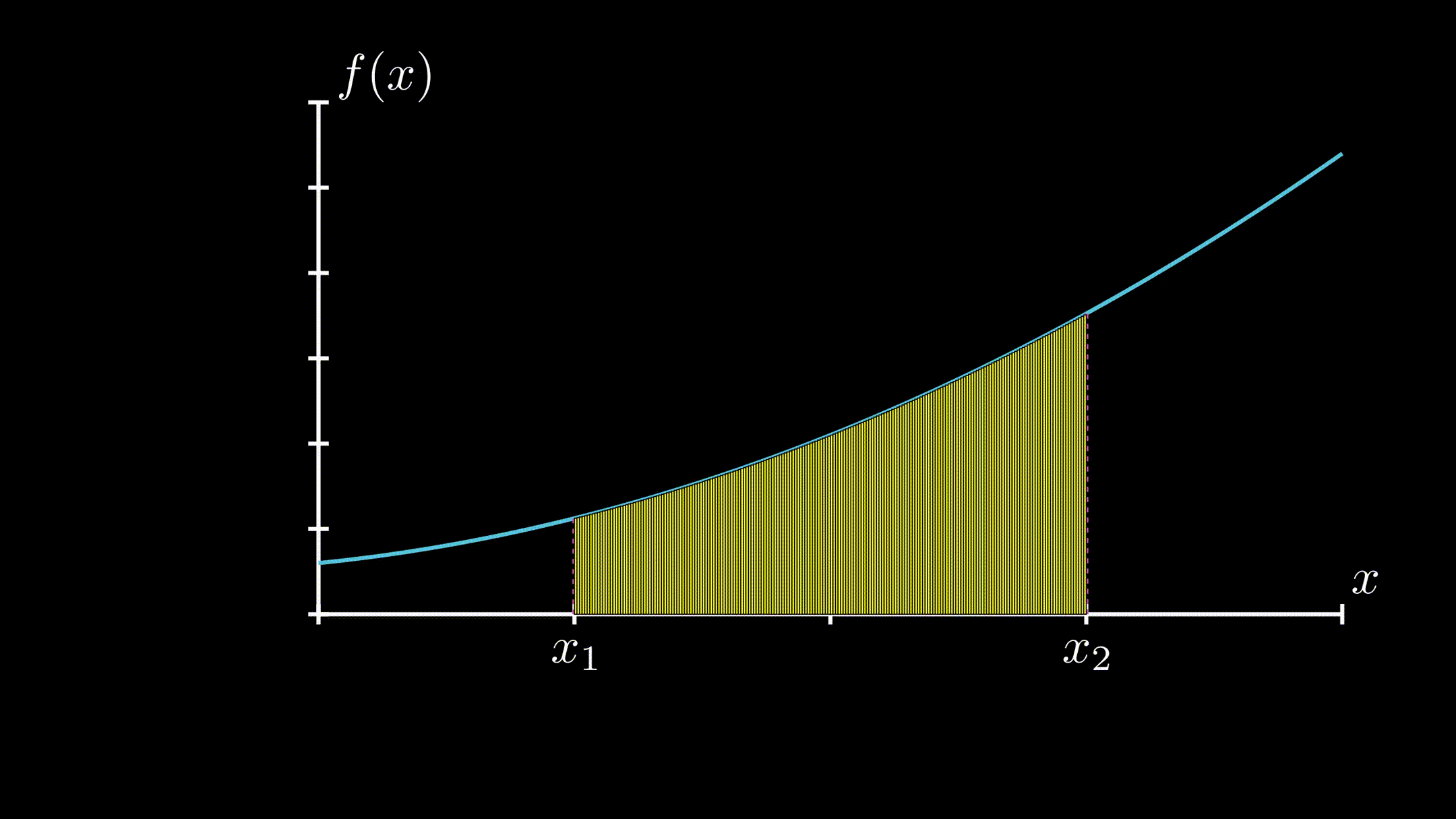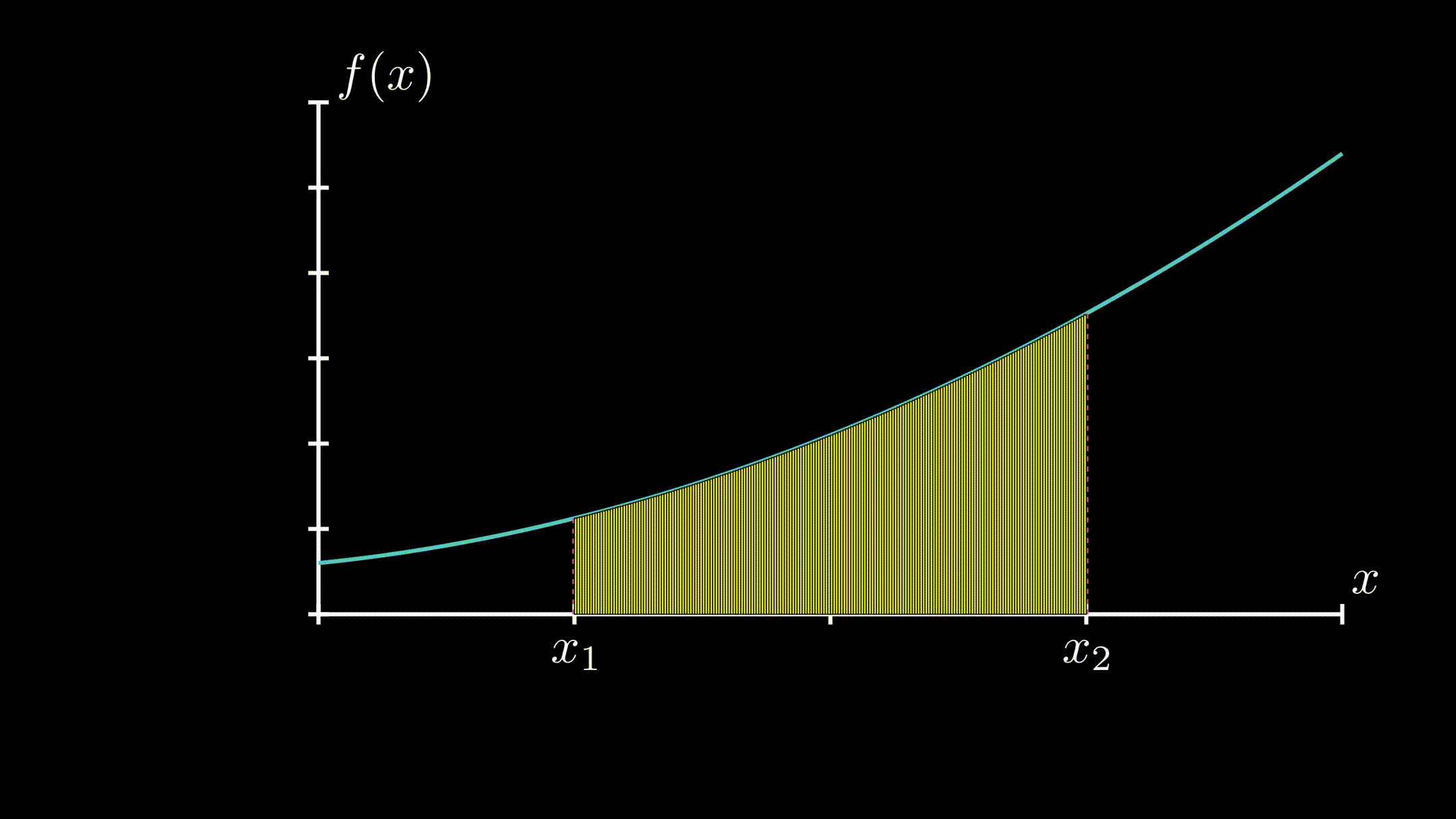 + + +RiemannRectanglesAnimation. + + + +mimi.gif +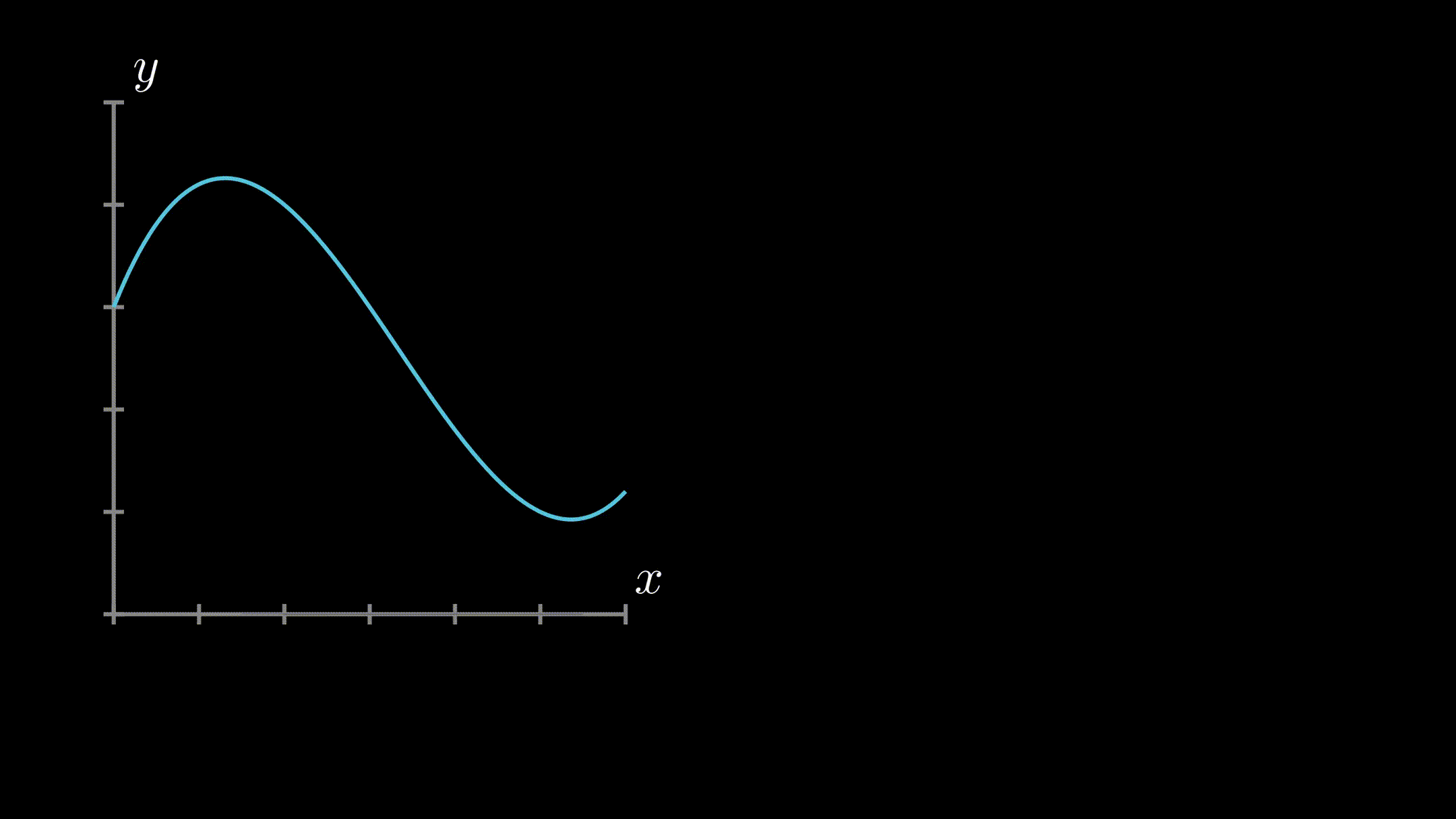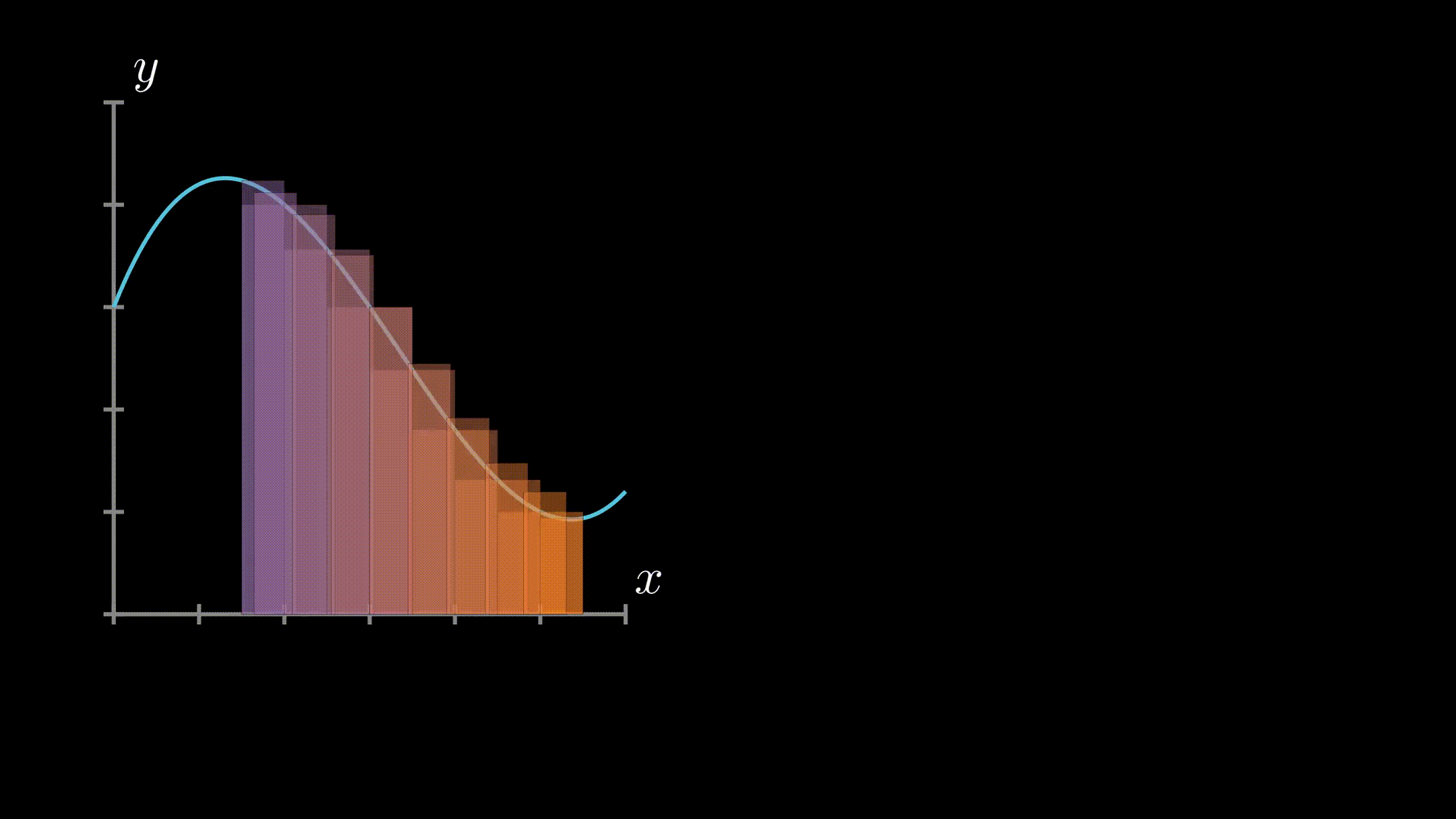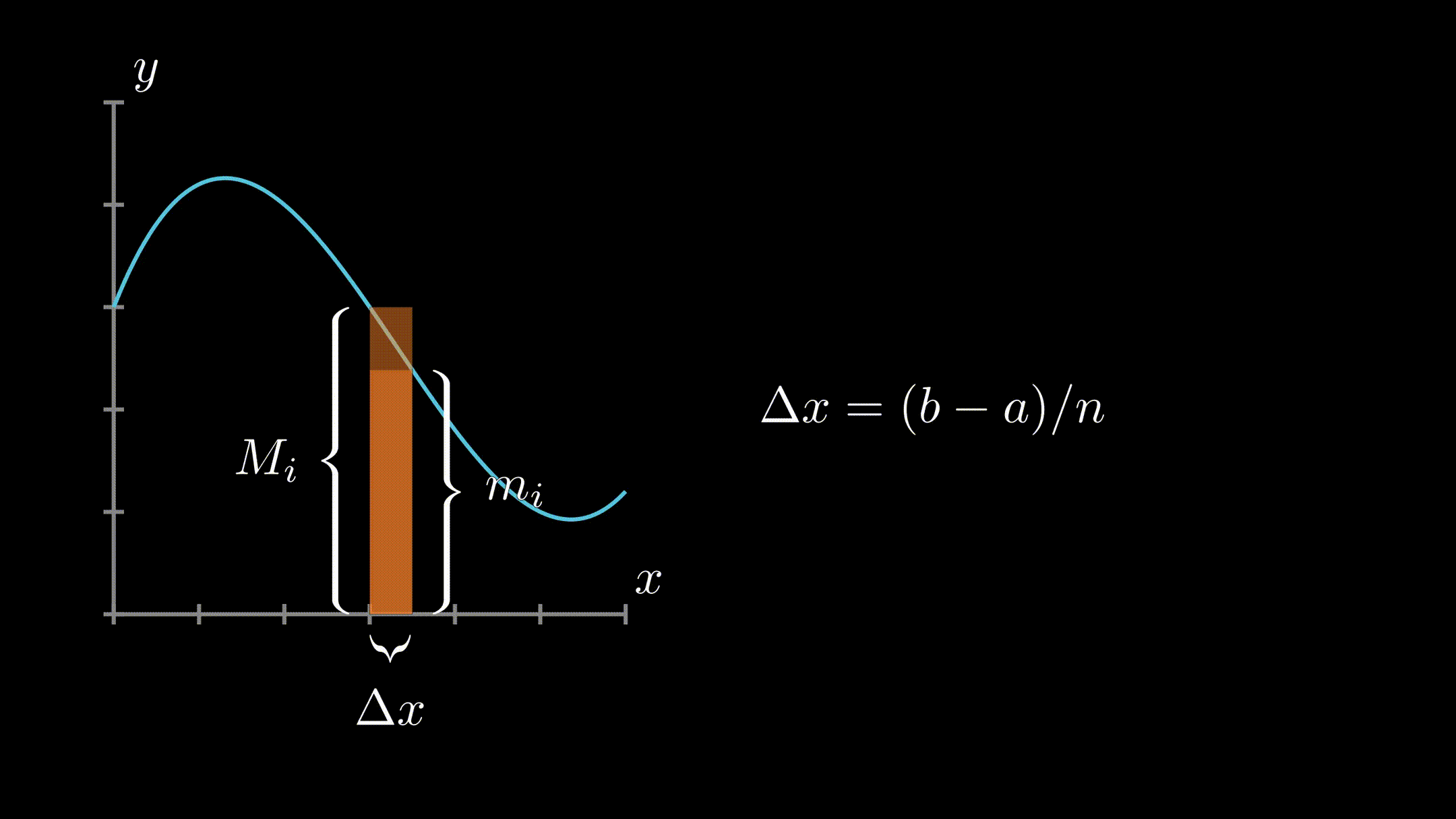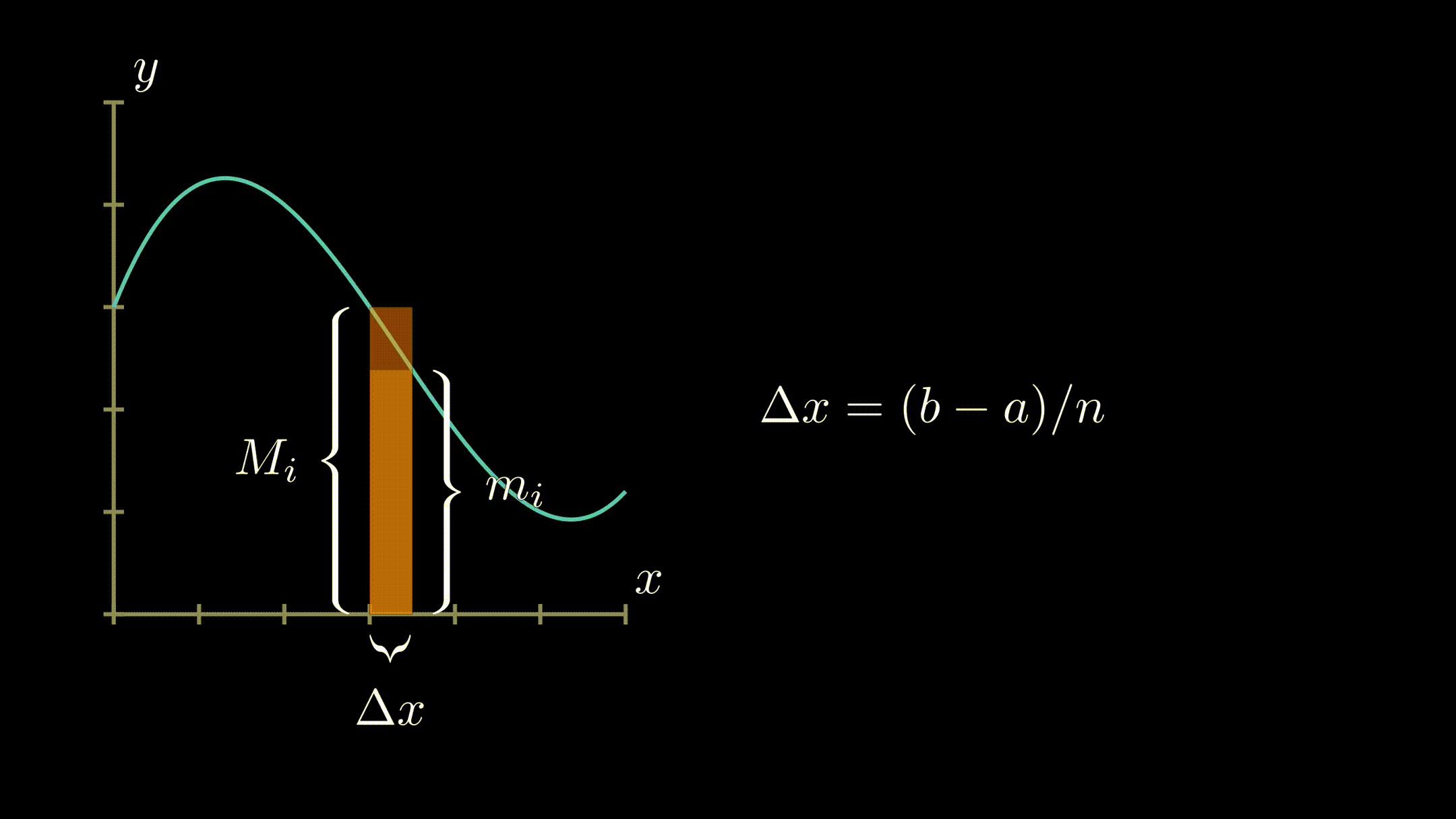 diff --git a/FSF-2020/calculus/intro-to-calculus/riemannintegrals/rierect1.py b/FSF-2020/calculus/intro-to-calculus/riemannintegrals/rierect1.py new file mode 100644 index 0000000..748d766 --- /dev/null +++ b/FSF-2020/calculus/intro-to-calculus/riemannintegrals/rierect1.py @@ -0,0 +1,31 @@ +from manimlib.imports import * +class rierect1(GraphScene): + CONFIG = { + "y_max" : 6, + "y_min" : 0, + "x_max" : 4, + "x_min" : 0, + "y_tick_frequency" : 1, + "x_tick_frequency" : 1, + "axes_color" : WHITE, + "num_graph_anchor_points": 3000, #this is the number of points that graph manim + "graph_origin" : ORIGIN+2*DOWN+4*LEFT, + "x_labeled_nums": None,#list(range(-1,2)), + "y_labeled_nums": None,#list(range(0,2)), + "x_axis_label":"$x$", + "y_axis_label":"$f(x)$", + "x_axis_width": 10, + "y_axis_height": 5, + } + def construct(self): + self.setup_axes() + graph1 = self.get_graph(lambda x : (0.1*(1.5*x+1)**2 +0.5), x_min = 0, x_max = 4) + minlim = self.get_vertical_line_to_graph(1,graph1,DashedLine, color = PINK) + maxlim = self.get_vertical_line_to_graph(3,graph1,DashedLine,color = PINK) + x1 = TexMobject(r"{x}_{1}").next_to(minlim, DOWN) + x2 = TexMobject(r"{x}_{2}").next_to(maxlim, DOWN) + rie1 = self.get_riemann_rectangles(graph1, x_min = 1, x_max = 3, dx = 0.4, input_sample_type = "left", fill_opacity = 1, start_color = YELLOW, end_color = YELLOW) + #rie2 = self.get_riemann_rectangles(graph1, x_min = 1, x_max = 3, dx = 0.01, input_sample_type = "right", fill_opacity = 0.5, start_color = PINK, end_color = LIGHT_PINK) + group = VGroup(graph1, minlim, maxlim, x1, x2, rie1) + self.play(ShowCreation(group)) + self.wait(1.5) diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/README.md b/FSF-2020/calculus/series-and-transformations/Fourier Transform/README.md new file mode 100644 index 0000000..2fa4e04 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/README.md @@ -0,0 +1,20 @@ +### Dividing a tone into its constituents + + +### Colors Analogy + + +### Applying the same on Graphs + + +### Fourier series for non-periodic functions-a + + +### Fourier series for non-periodic functions-b + + +### Fourier Series of Square pulse + + +### Coins Analogy + diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file1.gif b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file1.gif Binary files differnew file mode 100644 index 0000000..d4dc9d7 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file1.gif diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file2a.gif b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file2a.gif Binary files differnew file mode 100644 index 0000000..8f83bc4 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file2a.gif diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file2b.gif b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file2b.gif Binary files differnew file mode 100644 index 0000000..d68c405 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file2b.gif diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file3.gif b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file3.gif Binary files differnew file mode 100644 index 0000000..de94810 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file3.gif diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file4.gif b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file4.gif Binary files differnew file mode 100644 index 0000000..36cd61b --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file4.gif diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file5.gif b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file5.gif Binary files differnew file mode 100644 index 0000000..9757bd6 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file5.gif diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file6.gif b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file6.gif Binary files differnew file mode 100644 index 0000000..de94810 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file6.gif diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file7.gif b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file7.gif Binary files differnew file mode 100644 index 0000000..ab4eed8 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/gifs/file7.gif diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/video1_DividingAToneIntoItsConstituents.py b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video1_DividingAToneIntoItsConstituents.py new file mode 100644 index 0000000..39db6d8 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video1_DividingAToneIntoItsConstituents.py @@ -0,0 +1,90 @@ +from manimlib.imports import* +import numpy as np + +# def func(t,n): +# s=0 +# for i in range(1,n+1): +# s+=((-2/(i*np.pi))*((-1)**i)*np.sin(2*np.pi*i*t)) +# return s + + +class intro(GraphScene): + CONFIG = { + "x_min": -3, + "x_max": 3, + "x_axis_width": 6, + "y_min": -5, + "y_max": 5, + "graph_origin": 10.5*LEFT, + "axes_color": BLUE, + "exclude_zero_label": True, + "x_labeled_nums": range(-2, 3, 1), + } + def func(self,t,n1,n2): + s=0 + for i in range(n1,n2+1): + s+=((-2/(i*np.pi))*((-1)**i)*np.sin(2*np.pi*i*t)) + return s + + def construct(self): + image=ImageMobject('image.png').shift(5.5*LEFT+2.5*UP).scale(1.5) + self.play(ShowCreation(image)) + + self.setup_axes(scalee=1) + + mainGraphs=[ + self.get_graph(lambda x:self.func(x,2,7),x_max=2,x_min=-2).shift(9.3*RIGHT+3*UP).set_color([ORANGE,GREEN_B,RED_E,YELLOW_E,RED_D,YELLOW_D]).scale(1.4), + self.get_graph(lambda x:self.func(x,3,7),x_max=2,x_min=-2).shift(10.8*RIGHT+3*UP).set_color([GREEN_B,ORANGE,RED_D,YELLOW_E,YELLOW_D]).scale(1.4), + self.get_graph(lambda x:self.func(x,4,7),x_max=2,x_min=-2).shift(10.8*RIGHT+3*UP).set_color([GREEN_B,YELLOW_E,ORANGE,YELLOW_D]).scale(1.4), + self.get_graph(lambda x:self.func(x,5,7),x_max=2,x_min=-2).shift(10.8*RIGHT+3*UP).set_color([YELLOW_E,GREEN_B,YELLOW_D]).scale(1.4), + self.get_graph(lambda x:self.func(x,6,7),x_max=2,x_min=-2).shift(10.8*RIGHT+3*UP).set_color([YELLOW_D,GREEN_B]).scale(1.4), + self.get_graph(lambda x:self.func(x,7,7),x_max=2,x_min=-2,color=GREEN_B).shift(10.8*RIGHT+3*UP).scale(1.4), + ] + self.play(ApplyMethod(mainGraphs[0].shift,1.5*RIGHT)) + + graph1=self.get_graph(lambda x:self.func(x,2,2),x_max=2,x_min=-2,color=RED_E).shift(10.8*RIGHT+3*UP).scale(1.5) + graph2=self.get_graph(lambda x:self.func(x,3,3),x_max=2,x_min=-2,color=RED_D).shift(10.8*RIGHT+3*UP).scale(1.5) + graph3=self.get_graph(lambda x:self.func(x,4,4),x_max=2,x_min=-2,color=ORANGE).shift(10.8*RIGHT+3*UP).scale(1.5) + graph4=self.get_graph(lambda x:self.func(x,5,5),x_max=2,x_min=-2,color=YELLOW_E).shift(10.8*RIGHT+3*UP).scale(1.5) + graph5=self.get_graph(lambda x:self.func(x,6,6),x_max=2,x_min=-2,color=YELLOW_D).shift(10.8*RIGHT+3*UP).scale(1.5) + + coeff=[ + TextMobject("$\\frac { -1 }{ \pi } sin(4\pi t)$").scale(0.5).shift(DOWN+4.6*RIGHT+3*UP).set_color(RED_E), + TextMobject("$\\frac { 2 }{ 3\pi } sin(6\pi t)$").scale(0.5).shift(2*DOWN+4.6*RIGHT+3*UP).set_color(RED_D), + TextMobject("$\\frac { -1 }{ 2\pi } sin(8\pi t)$").scale(0.5).shift(3*DOWN+4.6*RIGHT+3*UP).set_color(ORANGE), + TextMobject("$\\frac { 2 }{ 5\pi } sin(10\pi t)$").scale(0.5).shift(4*DOWN+4.6*RIGHT+3*UP).set_color(YELLOW_E), + TextMobject("$\\frac { -1 }{ 3\pi } sin(12\pi t)$").scale(0.5).shift(5*DOWN+4.6*RIGHT+3*UP).set_color(YELLOW_D), + TextMobject("$\\frac { 2 }{ 7\pi } sin(14\pi t)$").scale(0.5).shift(6*DOWN+4.6*RIGHT+3*UP).set_color(GREEN_B) + ] + + self.wait(0.6) + self.play(ApplyMethod(graph1.shift,1*DOWN),ReplacementTransform(mainGraphs[0],mainGraphs[1])) + self.play(Write(coeff[0])) + self.play(ApplyMethod(graph2.shift,2*DOWN),ReplacementTransform(mainGraphs[1],mainGraphs[2])) + self.play(Write(coeff[1])) + self.play(ApplyMethod(graph3.shift,3*DOWN),ReplacementTransform(mainGraphs[2],mainGraphs[3])) + self.play(Write(coeff[2])) + self.play(ApplyMethod(graph4.shift,4*DOWN),ReplacementTransform(mainGraphs[3],mainGraphs[4])) + self.play(Write(coeff[3])) + self.play(ApplyMethod(graph5.shift,5*DOWN),ReplacementTransform(mainGraphs[4],mainGraphs[5])) + self.play(Write(coeff[4])) + self.play(ApplyMethod(mainGraphs[5].shift,6*DOWN)) + self.play(Write(coeff[5])) + + pluses=[TextMobject("+"),TextMobject("+"),TextMobject("+"),TextMobject("+"),TextMobject("+")] + for t in pluses: + t.scale(0.5).shift((2.2-1.5*pluses.index(t))*LEFT) + + finalGraph=self.get_graph(lambda x:self.func(x,2,7),x_max=2,x_min=-2).shift(10.8*RIGHT+3*UP) + finalGraph.set_color([GREEN_B,YELLOW_D,YELLOW_E,ORANGE,RED_D,RED_E]) + finalGroup=VGroup(graph1,graph2,graph3,graph4,graph5,mainGraphs[5]) + self.play(ReplacementTransform(finalGroup,finalGraph)) + self.play(ApplyMethod(coeff[0].scale,0.7),ApplyMethod(coeff[1].scale,0.7),ApplyMethod(coeff[2].scale,0.7),ApplyMethod(coeff[3].scale,0.7),ApplyMethod(coeff[4].scale,0.7),ApplyMethod(coeff[5].scale,0.7)) + #self.play(ApplyMethod(coeff[0].shift,7*LEFT+1.6*DOWN),ApplyMethod(coeff[1].shift,5.5*LEFT+0.8*DOWN),ApplyMethod(coeff[2].shift,4*LEFT),ApplyMethod(coeff[3].shift,2.5*LEFT+0.8*UP),ApplyMethod(coeff[4].shift,LEFT+1.6*UP),ApplyMethod(coeff[5].shift,0.5*RIGHT+2.4*DOWN)) + self.play(ApplyMethod(coeff[0].shift,7.6*LEFT+2*DOWN),ApplyMethod(coeff[1].shift,6.1*LEFT+DOWN),ApplyMethod(coeff[2].shift,4.6*LEFT),ApplyMethod(coeff[3].shift,3.1*LEFT+UP),ApplyMethod(coeff[4].shift,1.6*LEFT+2*UP),ApplyMethod(coeff[5].shift,0.1*LEFT+3*UP)) + equal=TextMobject("=").scale(1.5).shift(1.5*UP) + self.play(Write(equal)) + self.play(Write(pluses[0]),Write(pluses[1]),Write(pluses[2]),Write(pluses[3]),Write(pluses[4])) + group=VGroup(pluses[0],pluses[1],pluses[2],pluses[3],pluses[4],coeff[0],coeff[1],coeff[2],coeff[3],coeff[4],coeff[5]) + self.play(ApplyMethod(group.scale,1.5)) + self.wait(2) diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/video2_ColorsAnalogyForFourierSeries.py b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video2_ColorsAnalogyForFourierSeries.py new file mode 100644 index 0000000..8f3706b --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video2_ColorsAnalogyForFourierSeries.py @@ -0,0 +1,165 @@ +from manimlib.imports import* +import numpy as np + +def func(t,n1,n2): + s=0 + for i in range(n1,n2+1): + s+=((-2/(i*np.pi))*((-1)**i)*np.sin(2*np.pi*i*t)) + return s + +class divideColors(GraphScene): + CONFIG = { + "x_min": -2, + "x_max": 2, + "y_min": -1, + "y_max": 1, + "graph_origin": ORIGIN, + "function_color": RED, + "axes_color": BLUE, + "x_axis_label": "$t$", + "y_axis_label": "$y$", + "x_labeled_nums": range(-1, 2, 1), + "x_axis_width": 3, + "y_axis_height": 2 + } + def construct(self): + text1a=TextMobject("Consider dividing a","mixture of colors") + text1b=TextMobject("into its","components") + text1a.scale(0.8) + text1b.scale(0.8) + text1a.shift(UP) + text1b.shift(0.3*UP) + text1a.set_color_by_tex_to_color_map({"mixture of colors":[GREEN,RED,BLUE,YELLOW]}) + text1b.set_color_by_tex_to_color_map({"components":GREEN}) + self.play(Write(text1a)) + self.play(FadeIn(text1b)) + self.wait(0.8) + + self.play(FadeOut(text1a),FadeOut(text1b)) + + mainCircle=Circle(radius=1.4,color=BLACK,fill_color=[PURPLE_E,PURPLE_D,RED_B,ORANGE,YELLOW_B,YELLOW_D,GREEN_A,GREEN_C],fill_opacity=0.8) + self.play(ShowCreation(mainCircle)) + self.wait(1) + mainCirclea=Circle(radius=1.4,color=BLACK,fill_color=[RED_B,ORANGE,YELLOW_B,YELLOW_D,GREEN_A,GREEN_C],fill_opacity=0.8) + mainCircleb=Circle(radius=1.4,color=BLACK,fill_color=[YELLOW_B,YELLOW_D,GREEN_A,GREEN_C],fill_opacity=0.8) + mainCirclec=Circle(radius=1.4,color=BLACK,fill_color=[GREEN_A,GREEN_C],fill_opacity=0.8) + mainCircled=Circle(radius=1.4,color=BLACK,fill_color=[],fill_opacity=0.8) + + c1=Circle(radius=0.5,color=PURPLE_E,fill_color=PURPLE_E,fill_opacity=0.8) + c2=Circle(radius=0.5,color=PURPLE_D,fill_color=PURPLE_D,fill_opacity=0.8) + c3=Circle(radius=0.5,color=RED_D,fill_color=RED_B,fill_opacity=0.8) + c4=Circle(radius=0.5,color=ORANGE,fill_color=ORANGE,fill_opacity=0.8) + c5=Circle(radius=0.5,color=YELLOW_B,fill_color=YELLOW_B,fill_opacity=0.8) + c6=Circle(radius=0.5,color=YELLOW_D,fill_color=YELLOW_D,fill_opacity=0.8) + c7=Circle(radius=0.5,color=GREEN_A,fill_color=GREEN_A,fill_opacity=0.8) + c8=Circle(radius=0.5,color=GREEN_C,fill_color=GREEN_C,fill_opacity=0.8) + + self.play(ApplyMethod(c1.shift,3*UP+LEFT),ApplyMethod(c2.shift,3*UP+RIGHT),ReplacementTransform(mainCircle,mainCirclea)) + self.wait(0.8) + + self.play(ApplyMethod(c3.shift,UP+3*LEFT),ApplyMethod(c4.shift,DOWN+3*LEFT),ReplacementTransform(mainCirclea,mainCircleb)) + self.wait(0.8) + + self.play(ApplyMethod(c5.shift,3*DOWN+LEFT),ApplyMethod(c6.shift,3*DOWN+RIGHT),ReplacementTransform(mainCircleb,mainCirclec)) + self.wait(0.8) + + self.play(ApplyMethod(c7.shift,3*RIGHT+UP),ApplyMethod(c8.shift,3*RIGHT+DOWN),ReplacementTransform(mainCirclec,mainCircled)) + self.wait(1) + + text2=TextMobject("Similarly,").scale(0.8).shift(UP).set_color(RED) + + self.play(FadeOut(c1),FadeOut(c2),FadeOut(c3),FadeOut(c4),FadeOut(c5),FadeOut(c6),FadeOut(c7),FadeOut(c8)) + self.play(Write(text2)) + self.wait(0.8) + self.play(FadeOut(text2)) + + + coeff=[ + TextMobject("$\\frac { -2 }{ \pi } \sum _{ n=1 }^{ 24 }{ \\frac { { -1 }^{ n } }{ n } sin(2\pi nt) }$").scale(0.2).shift(RIGHT+UP), + TextMobject("$\\frac { 2 }{ \pi } sin(2\pi t)$").scale(0.3).shift(RIGHT+UP+4*LEFT+UP), + TextMobject("$\\frac { -2 }{ \pi } \sum _{ n=2 }^{ 24 }{ \\frac { { -1 }^{ n } }{ n } sin(2\pi nt) }$").scale(0.2).shift(RIGHT+UP), + TextMobject("$\\frac { -1 }{ \pi } sin(4\pi t)$").scale(0.3).shift(RIGHT+UP+4*RIGHT+UP), + TextMobject("$\\frac { -2 }{ \pi } \sum _{ n=3 }^{ 24 }{ \\frac { { -1 }^{ n } }{ n } sin(2\pi nt) }$").scale(0.2).shift(RIGHT+UP), + TextMobject("$\\frac { 2 }{ 3\pi } sin(6\pi t)$").scale(0.3).shift(RIGHT+UP+4*LEFT+2*DOWN), + TextMobject("$\\frac { -2 }{ \pi } \sum _{ n=4 }^{ 24 }{ \\frac { { -1 }^{ n } }{ n } sin(2\pi nt) }$").scale(0.2).shift(RIGHT+UP), + TextMobject("$\\frac { -1 }{ 2\pi } sin(8\pi t)$").scale(0.3).shift(RIGHT+UP+4*RIGHT+2*DOWN), + TextMobject("$\\frac { -2 }{ \pi } \sum _{ n=5 }^{ 24 }{ \\frac { { -1 }^{ n } }{ n } sin(2\pi nt) }$").scale(0.2).shift(RIGHT+UP), + TextMobject("$\\frac { 2 }{ 5\pi } sin(10\pi t)$").scale(0.3).shift(RIGHT+UP+2.5*UP), + TextMobject("$\\frac { -2 }{ \pi } \sum _{ n=6 }^{ 24 }{ \\frac { { -1 }^{ n } }{ n } sin(2\pi nt) }$").scale(0.2).shift(RIGHT+UP), + TextMobject("$\\frac { -1 }{ 3\pi } sin(12\pi t)$").scale(0.3).shift(RIGHT+UP+2.5*DOWN), + TextMobject("$\\frac { -2 }{ \pi } \sum _{ n=7 }^{ 24 }{ \\frac { { -1 }^{ n } }{ n } sin(2\pi nt) }$").scale(0.2).shift(RIGHT+UP), + ] + + axes=[] + self.setup_axes(scalee=1) + axes.append(self.axes) + graphs=[self.get_graph(lambda x:func(x,1,24),x_min=-1,x_max=1).set_color([DARK_BROWN,GREEN_E,GREEN_C,GOLD_E,GOLD_C,ORANGE,RED_C]), + self.get_graph(lambda x:func(x,2,24),x_min=-1,x_max=1).set_color([DARK_BROWN,GREEN_C,GOLD_E,GOLD_C,ORANGE,RED_C]), + self.get_graph(lambda x:func(x,3,24),x_min=-1,x_max=1).set_color([DARK_BROWN,GOLD_E,GOLD_C,ORANGE,RED_C]), + self.get_graph(lambda x:func(x,4,24),x_min=-1,x_max=1).set_color([DARK_BROWN,GOLD_C,ORANGE,RED_C]), + self.get_graph(lambda x:func(x,5,24),x_min=-1,x_max=1).set_color([DARK_BROWN,ORANGE,RED_C]), + self.get_graph(lambda x:func(x,6,24),x_min=-1,x_max=1).set_color([DARK_BROWN,RED_C]), + self.get_graph(lambda x:func(x,7,24),x_min=-1,x_max=1).set_color(DARK_BROWN) + ] + #self.y_axis_label="$\\frac { 2 }{ \pi } sin(2\pi t)$" + self.setup_axes(scalee=1) + axes.append(self.axes) + graph1=self.get_graph(lambda x:func(x,1,1),x_min=-1,x_max=1,color=GREEN_E) + #self.y_axis_label="$\\frac { -1 }{ \pi } sin(4\pi t)$" + self.setup_axes(scalee=1) + axes.append(self.axes) + graph2=self.get_graph(lambda x:func(x,2,2),x_min=-1,x_max=1,color=GREEN_C) + #self.y_axis_label="$\\frac { 2 }{ 3\pi } sin(6\pi t)$" + self.setup_axes(scalee=1) + axes.append(self.axes) + graph3=self.get_graph(lambda x:func(x,3,3),x_min=-1,x_max=1,color=GOLD_E) + #self.y_axis_label="$\\frac { -1 }{ 2\pi } sin(8\pi t)$" + self.setup_axes(scalee=1) + axes.append(self.axes) + graph4=self.get_graph(lambda x:func(x,4,4),x_min=-1,x_max=1,color=GOLD_C) + #self.y_axis_label="$\\frac { 2 }{ 5\pi } sin(10\pi t)$" + self.setup_axes(scalee=1) + axes.append(self.axes) + graph5=self.get_graph(lambda x:func(x,5,5),x_min=-1,x_max=1,color=ORANGE) + #self.y_axis_label="$\\frac { -1 }{ 3\pi } sin(12\pi t)$" + self.setup_axes(scalee=1) + axes.append(self.axes) + graph6=self.get_graph(lambda x:func(x,6,6),x_min=-1,x_max=1,color=RED_C) + + groups=[VGroup(axes[1],graph1),VGroup(axes[2],graph2),VGroup(axes[3],graph3),VGroup(axes[4],graph4), + VGroup(axes[5],graph5),VGroup(axes[6],graph6)] + + self.play(ShowCreation(graphs[0])) + self.play(Write(coeff[0])) + self.wait(1) + # self.play(ApplyMethod(axes[0].scale,0.4),ApplyMethod(graphs[0].scale,0.4),ApplyMethod(axes[1].scale,0.4), + # ApplyMethod(axes[2].scale,0.4),ApplyMethod(axes[3].scale,0.4), + # ApplyMethod(axes[4].scale,0.4),ApplyMethod(axes[5].scale,0.4),ApplyMethod(axes[6].scale,0.4)) + self.play(ReplacementTransform(graphs[0],graphs[1]),ApplyMethod(groups[0].shift,4*LEFT+UP),ReplacementTransform(coeff[0],coeff[2]),FadeIn(coeff[1])) + self.play(ReplacementTransform(graphs[1],graphs[2]),ApplyMethod(groups[1].shift,4*RIGHT+UP),ReplacementTransform(coeff[2],coeff[4]),FadeIn(coeff[3])) + self.play(ReplacementTransform(graphs[2],graphs[3]),ApplyMethod(groups[2].shift,4*LEFT+2*DOWN),ReplacementTransform(coeff[4],coeff[6]),FadeIn(coeff[5])) + self.play(ReplacementTransform(graphs[3],graphs[4]),ApplyMethod(groups[3].shift,4*RIGHT+2*DOWN),ReplacementTransform(coeff[6],coeff[8]),FadeIn(coeff[7])) + self.play(ReplacementTransform(graphs[4],graphs[5]),ApplyMethod(groups[4].shift,2.5*UP),ReplacementTransform(coeff[8],coeff[10]),FadeIn(coeff[9])) + self.play(ReplacementTransform(graphs[5],graphs[6]),ApplyMethod(groups[5].shift,2.5*DOWN),ReplacementTransform(coeff[10],coeff[12]),FadeIn(coeff[11])) + + # self.play(ReplacementTransform(graphs[0],graphs[1]),ApplyMethod(groups[0].shift,3*LEFT)) + # self.play(ReplacementTransform(graphs[0],graphs[1]),) + # self.play(ReplacementTransform(graphs[0],graphs[1]),) + # self.play(ReplacementTransform(graphs[0],graphs[1]),) + # self.play(ReplacementTransform(graphs[0],graphs[1]),) + # self.play(ReplacementTransform(graphs[0],graphs[1]),) + + + + self.wait(2) + # self.play(ReplacementTransform(function,const)) + # self.play(ShowCreation(sinx),ShowCreation(cosx)) + # self.play(ShowCreation(sin2x),ShowCreation(cos2x)) + # self.play(ShowCreation(sin3x),ShowCreation(cos3x)) + # self.play(ShowCreation(sin4x),ShowCreation(cos4x)) + # sintext=TextMobject("Infinite","sines").shift(5*RIGHT).set_color_by_tex_to_color_map({"Infinite":[YELLOW,RED],"sines":BLUE}) + # costext=TextMobject("Infinite","cosines").shift(5*LEFT).set_color_by_tex_to_color_map({"Infinite":[YELLOW,RED],"cosines":BLUE}) + # sintext.scale(0.6) + # costext.scale(0.6) + # self.play(FadeIn(sintext),FadeIn(costext)) + # self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/video3_seriesVSTransform.py b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video3_seriesVSTransform.py new file mode 100644 index 0000000..07f884a --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video3_seriesVSTransform.py @@ -0,0 +1,146 @@ +from manimlib.imports import * +import numpy as np + +class compare(GraphScene,MovingCameraScene): + CONFIG = { + "x_min": -3, + "x_max": 3, + "x_axis_width": 6, + "y_min": -5, + "y_max": 5, + "y_axis_label":"$\\frac { { x }^{ 2 } }{ 2 } $", + "graph_origin": ORIGIN, + "axes_color": BLUE, + "exclude_zero_label": True, + "x_labeled_nums": range(-2, 3, 1), + } + def setup(self): + GraphScene.setup(self) + MovingCameraScene.setup(self) + def returnPairLines(self,left,right,y_each_unit): + lineLeft=DashedLine(start=(0,5*y_each_unit,0),end=(0,-5*y_each_unit,0)).shift(left) + lineRight=DashedLine(start=(0,5*y_each_unit,0),end=(0,-5*y_each_unit,0)).shift(right) + return lineLeft,lineRight + + def resultFunc(self,x,n,l): + s=(l**2)/6 + for n in range(1,n+1): + s+=(2*((-1)**n))*((l**2)*np.cos(n*np.pi*x/l))*(1/((np.pi**2)*(n**2))) + return s + + def returnPartFunction(self,left,right): + return self.get_graph(lambda x:(x**2)/2,x_min=left,x_max=right,color=RED) + + def returnPartResult(self,l,n): + return self.get_graph(lambda x:self.resultFunc(x,n,l),x_min=-3,x_max=3,color=RED) + + def construct(self): + x_each_unit = self.x_axis_width / (self.x_max - self.x_min) + y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + axes=[] + self.setup_axes(animate=True,scalee=1) + axes.append(self.axes) + partFunction1=self.returnPartFunction(-1,1).shift(4*LEFT) + partFunction2=self.returnPartFunction(-2,2).shift(4*LEFT) + functionText=TextMobject("$\\frac { { x }^{ 2 } }{ 2 } $") + function=self.get_graph(lambda x:(x**2)/2,x_min=-3,x_max=3,color=GREEN) + text1=TextMobject("Non-Periodic function").scale(0.5).shift(3*DOWN+3*RIGHT).set_color(RED) + self.play(ShowCreation(function)) + self.play(FadeIn(text1)) + self.wait(1) + self.play(FadeOut(text1)) + self.play(ApplyMethod(axes[0].shift,4*LEFT),ApplyMethod(function.shift,4*LEFT)) + text2=TextMobject("For a","given","interval of $x$,").scale(0.5).shift(2.5*RIGHT+UP).set_color_by_tex_to_color_map({"given":YELLOW,"interval of $x$,":BLUE}) + text3=TextMobject("We can get the","Fourier Series","of that","particular part!").scale(0.4).shift(2.5*RIGHT+0.5*UP).set_color_by_tex_to_color_map({"particular part!":YELLOW,"Fourier Series":RED}) + self.play(Write(text2)) + left,right=self.returnPairLines((4+x_each_unit)*LEFT,(4-x_each_unit)*LEFT,y_each_unit) + self.play(ShowCreation(left),ShowCreation(right)) + self.play(Write(text3)) + self.wait(0.5) + self.play(FadeOut(text2),FadeOut(text3)) + self.graph_origin=3.5*RIGHT + self.y_axis_label="$\\frac { { l }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ \infty }{ \\frac { 2{ (-1) }^{ n }{ l }^{ 2 }cos(\\frac { n\pi x }{ l } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } }$" + self.setup_axes(animate=True,scalee=1) + axes.append(self.axes) + coeffResult=[ + TextMobject("$\\frac { { 1 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 1 }{ \\frac { 2{ (-1) }^{ n }{ 1 }^{ 2 }cos(\\frac { n\pi x }{ 1 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.3).shift(4.5*RIGHT+UP).set_color(YELLOW), + TextMobject("$\\frac { { 1 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 3 }{ \\frac { 2{ (-1) }^{ n }{ 1 }^{ 2 }cos(\\frac { n\pi x }{ 1 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.3).shift(4.5*RIGHT+UP).set_color(YELLOW), + TextMobject("$\\frac { { 1 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 5 }{ \\frac { 2{ (-1) }^{ n }{ 1 }^{ 2 }cos(\\frac { n\pi x }{ 1 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.3).shift(4.5*RIGHT+UP).set_color(YELLOW), + TextMobject("$\\frac { { 1 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 7 }{ \\frac { 2{ (-1) }^{ n }{ 1 }^{ 2 }cos(\\frac { n\pi x }{ 1 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.3).shift(4.5*RIGHT+UP).set_color(YELLOW), + TextMobject("$\\frac { { 1 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 9 }{ \\frac { 2{ (-1) }^{ n }{ 1 }^{ 2 }cos(\\frac { n\pi x }{ 1 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.3).shift(4.5*RIGHT+UP).set_color(YELLOW), + TextMobject("$\\frac { { 1 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 11 }{ \\frac { 2{ (-1) }^{ n }{ 1 }^{ 2 }cos(\\frac { n\pi x }{ 1 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } }$").scale(0.3).shift(4.5*RIGHT+UP).set_color(YELLOW), + TextMobject("$\\frac { { 1 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 13 }{ \\frac { 2{ (-1) }^{ n }{ 1 }^{ 2 }cos(\\frac { n\pi x }{ 1 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } }$").scale(0.3).shift(4.5*RIGHT+UP).set_color(YELLOW) + ] + result1a=self.returnPartResult(1,1) + result1b=self.returnPartResult(1,3) + result1c=self.returnPartResult(1,5) + result1d=self.returnPartResult(1,7) + result1e=self.returnPartResult(1,9) + result1f=self.returnPartResult(1,11) + result1g=self.returnPartResult(1,13) + self.play(ApplyMethod(partFunction1.shift,0.2*UP)) + self.wait(0.5) + + self.play(ReplacementTransform(partFunction1,result1a),Write(coeffResult[0])) + self.play(FadeOut(axes[0]),FadeOut(left),FadeOut(right),FadeOut(function)) + self.camera_frame.save_state() + self.play(self.camera_frame.set_width, 5,self.camera_frame.move_to, 3.5*RIGHT) + + + self.play(ReplacementTransform(result1a,result1b),ReplacementTransform(coeffResult[0],coeffResult[1])) + self.play(ReplacementTransform(result1b,result1c),ReplacementTransform(coeffResult[1],coeffResult[2])) + self.play(ReplacementTransform(result1c,result1d),ReplacementTransform(coeffResult[2],coeffResult[3])) + self.play(ReplacementTransform(result1d,result1e),ReplacementTransform(coeffResult[3],coeffResult[4])) + self.play(ReplacementTransform(result1e,result1f),ReplacementTransform(coeffResult[4],coeffResult[5])) + self.play(ReplacementTransform(result1f,result1g),ReplacementTransform(coeffResult[5],coeffResult[6])) + + self.wait(0.5) + self.play(self.camera_frame.set_width, 14,self.camera_frame.move_to, 0) + + text4=TextMobject("Here the","obtained function","will always be","periodic","with period equal to the chosen interval").scale(0.4).shift(3.3*DOWN).set_color_by_tex_to_color_map({"obtained function":YELLOW,"periodic":RED}) + self.play(Write(text4)) + + self.wait(0.8) + + self.play(FadeOut(text4)) + text5=TextMobject("As we","increase","the","interval of $x$,").scale(0.5).shift(3*DOWN).set_color_by_tex_to_color_map({"increase":RED,"interval of $x$,":YELLOW}) + text6=TextMobject("We get","approximation","for","higher intervals!").scale(0.5).shift(3.5*DOWN).set_color_by_tex_to_color_map({"approximation":GREEN,"higher intervals!":YELLOW}) + self.play(FadeIn(axes[0]),FadeIn(left),FadeIn(right),FadeIn(function)) + self.play(Write(text5)) + self.play(Write(text6)) + result2=self.returnPartResult(1.5,20) + result3=self.returnPartResult(2,20) + result4=self.returnPartResult(2.5,20) + result5=self.returnPartResult(3,20) + finalCoeff=coeffResult[6] + coeffResult=[ + TextMobject("$\\frac { { 1.5 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 20 }{ \\frac { 2{ (-1) }^{ n }{ 1.5 }^{ 2 }cos(\\frac { n\pi x }{ 2 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } }$").scale(0.4).shift(5*RIGHT+1.5*UP).set_color(YELLOW), + TextMobject("$\\frac { { 2 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 20 }{ \\frac { 2{ (-1) }^{ n }{ 2 }^{ 2 }cos(\\frac { n\pi x }{ 2 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.4).shift(5*RIGHT+1.5*UP).set_color(YELLOW), + TextMobject("$\\frac { { 2.5 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 20 }{ \\frac { 2{ (-1) }^{ n }{ 2.5 }^{ 2 }cos(\\frac { n\pi x }{ 2 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.4).shift(5*RIGHT+2.2*UP).set_color(YELLOW), + TextMobject("$\\frac { { 3 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 20 }{ \\frac { 2{ (-1) }^{ n }{ 3 }^{ 2 }cos(\\frac { n\pi x }{ 2 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.4).shift(5*RIGHT+2.2*UP).set_color(YELLOW), + ] + self.play(ApplyMethod(left.shift,LEFT*x_each_unit*0.5),ApplyMethod(right.shift,RIGHT*x_each_unit*0.5),ReplacementTransform(result1g,result2),ReplacementTransform(finalCoeff,coeffResult[0])) + self.play(ApplyMethod(left.shift,LEFT*x_each_unit*0.5),ApplyMethod(right.shift,RIGHT*x_each_unit*0.5),ReplacementTransform(result2,result3),ReplacementTransform(coeffResult[0],coeffResult[1])) + self.play(ApplyMethod(left.shift,LEFT*x_each_unit*0.5),ApplyMethod(right.shift,RIGHT*x_each_unit*0.5),ReplacementTransform(result3,result4),ReplacementTransform(coeffResult[1],coeffResult[2])) + self.play(ApplyMethod(left.shift,LEFT*x_each_unit*0.5),ApplyMethod(right.shift,RIGHT*x_each_unit*0.5),ReplacementTransform(result4,result5),ReplacementTransform(coeffResult[2],coeffResult[3])) + + + # coeffResult=[ + # TextMobject("$\\frac { { 2 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 1 }{ \\frac { 2{ (-1) }^{ n }{ 2 }^{ 2 }cos(\\frac { n\pi x }{ 2 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } }$").scale(0.3).shift(4.5*RIGHT+1.5*UP), + # TextMobject("$\\frac { { 2 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 4 }{ \\frac { 2{ (-1) }^{ n }{ 2 }^{ 2 }cos(\\frac { n\pi x }{ 2 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.3).shift(4.5*RIGHT+1.5*UP), + # TextMobject("$\\frac { { 2 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 10 }{ \\frac { 2{ (-1) }^{ n }{ 2 }^{ 2 }cos(\\frac { n\pi x }{ 2 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.3).shift(4.5*RIGHT+1.5*UP), + # TextMobject("$\\frac { { 2 }^{ 2 } }{ 6 } +\sum _{ n=1 }^{ 20 }{ \\frac { 2{ (-1) }^{ n }{ 2 }^{ 2 }cos(\\frac { n\pi x }{ 2 } ) }{ { \pi }^{ 2 }{ n }^{ 2 } } } $").scale(0.3).shift(4.5*RIGHT+1.5*UP), + # ] + # result2a=self.returnPartResult(2,1) + # result2b=self.returnPartResult(2,4) + # result2c=self.returnPartResult(2,10) + # result2d=self.returnPartResult(2,20) + + # self.play(ReplacementTransform(partFunction2,result2a),ReplacementTransform(coeffResult[0],coeffResult[1])) + # self.play(ReplacementTransform(result2a,result2b),ReplacementTransform(coeffResult[0],coeffResult[1])) + # self.play(ReplacementTransform(result2b,result2c),ReplacementTransform(coeffResult[0],coeffResult[1])) + # self.play(ReplacementTransform(result2c,result2d),ReplacementTransform(coeffResult[0],coeffResult[1])) + # self.wait(0.5) + + + self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/video4_FourierSeriesOfSquarePulse.py b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video4_FourierSeriesOfSquarePulse.py new file mode 100644 index 0000000..fdf4bb3 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video4_FourierSeriesOfSquarePulse.py @@ -0,0 +1,97 @@ +from manimlib.imports import * +import numpy as np + +def returnSum(k,x): + summ=0 + for i in range(1,k+1,2): + summ+=((np.sin(2*np.pi*i*x))/i) + return summ + +def returnFunc(self,k): + graph=self.get_graph(lambda x:(4/np.pi)*returnSum(k,x),color=WHITE,x_max=1,x_min=-1) + return graph + +class fourierSeries(GraphScene,MovingCameraScene): + CONFIG = { + "x_min": -3, + "x_max": 3, + "x_axis_width": 13, + "y_min": -3, + "y_max": 3, + "graph_origin": ORIGIN, + "function_color": RED, + "axes_color": BLUE, + "x_axis_label": "$x$", + "y_axis_label": "$y$", + "exclude_zero_label": True, + "x_labeled_nums": range(-2, 3, 1), + } + def setup(self): + GraphScene.setup(self) + MovingCameraScene.setup(self) + def construct(self): + x_each_unit = self.x_axis_width / (self.x_max - self.x_min) + y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + + equation=TextMobject("$f(x)=\\frac { 4 }{ \pi } \sum _{ k=1,3,5.. }^{ \infty }{ \\frac { 1 }{ k } \sin { 2\pi kx } }$").shift(5*RIGHT+3*UP).set_color(RED).scale(0.5) + self.add(equation) + self.setup_axes(animate=True,scalee=1) + line1=Line(start=(-x_each_unit,y_each_unit,0),end=(-(1/2)*x_each_unit,y_each_unit,0),color=RED) + line2=Line(start=(-(1/2)*x_each_unit,y_each_unit,0),end=(-(1/2)*x_each_unit,-y_each_unit,0),color=RED) + line3=Line(start=(-(1/2)*x_each_unit,-y_each_unit,0),end=(0,-y_each_unit,0),color=RED) + line4=Line(start=(0,-y_each_unit,0),end=(0,y_each_unit,0),color=RED) + line5=Line(start=(0,y_each_unit,0),end=((1/2)*x_each_unit,y_each_unit,0),color=RED) + line6=Line(start=((1/2)*x_each_unit,y_each_unit,0),end=((1/2)*x_each_unit,-y_each_unit,0),color=RED) + line7=Line(start=((1/2)*x_each_unit,-y_each_unit,0),end=(x_each_unit,-y_each_unit,0),color=RED) + self.play(ShowCreation(line1)) + self.play(ShowCreation(line2)) + self.play(ShowCreation(line3)) + self.play(ShowCreation(line4)) + self.play(ShowCreation(line5)) + self.play(ShowCreation(line6)) + self.play(ShowCreation(line7)) + self.wait(0.5) + + labels=[ + TextMobject("$f_{ k=1 }(x)$"), + TextMobject("$f_{ k=3 }(x)$"), + TextMobject("$f_{ k=5 }(x)$"), + TextMobject("$f_{ k=7 }(x)$"), + TextMobject("$f_{ k=9 }(x)$"), + TextMobject("$f_{ k=11 }(x)$"), + TextMobject("$f_{ k=13 }(x)$"), + TextMobject("$f_{ k=15 }(x)$"), + TextMobject("$f_{ k=17 }(x)$"), + TextMobject("$f_{ k=19 }(x)$"), + TextMobject("$f_{ k=85 }(x)$") + ] + p=0 + for i in range(1,20,2): + if(i==1): + graphInitial=returnFunc(self,1) + label=labels[p].scale(0.5).shift(y_each_unit*1.5*UP+RIGHT*x_each_unit*0.3) + self.play(ShowCreation(graphInitial),Write(labels[0])) + old=graphInitial + oldLabel=label + else: + graph=returnFunc(self,i) + graphLabel=labels[p].scale(0.5).shift(y_each_unit*1.5*UP+RIGHT*x_each_unit*0.3) + self.play(ReplacementTransform(old,graph),ReplacementTransform(oldLabel,graphLabel)) + old=graph + oldLabel=graphLabel + p+=1 + graphFinal=returnFunc(self,85) + labelFinal=labels[10].scale(0.5).shift(y_each_unit*1.5*UP+RIGHT*x_each_unit*0.3) + self.play(FadeOut(old),FadeOut(oldLabel)) + self.play(ShowCreation(graphFinal),Write(labelFinal)) + self.wait(1) + self.camera_frame.save_state() + self.play(self.camera_frame.set_width, 2.25,self.camera_frame.move_to, y_each_unit*UP+RIGHT*x_each_unit*0.3) + circleMark=Circle(radius=0.1,color=GREEN).shift(x_each_unit*RIGHT*0.47+UP*y_each_unit*1.1) + text=TextMobject("Gibbs","phenomenon").set_color_by_tex_to_color_map({"Gibbs":BLUE,"phenomenon":YELLOW}).scale(0.1).shift(RIGHT*x_each_unit*0.65+UP*y_each_unit*1.1) + self.wait(0.7) + self.play(ShowCreation(circleMark)) + self.play(Write(text)) + self.wait(0.5) + self.play(self.camera_frame.set_width,14,self.camera_frame.move_to,0,FadeOut(circleMark),FadeOut(text)) + self.wait(2) diff --git a/FSF-2020/calculus/series-and-transformations/Fourier Transform/video5_CoinsAnalogy.py b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video5_CoinsAnalogy.py new file mode 100644 index 0000000..10ee889 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Fourier Transform/video5_CoinsAnalogy.py @@ -0,0 +1,225 @@ +from manimlib.imports import* +import math +import numpy as np + +class coinsAnalogy(Scene): + def construct(self): + text1=TextMobject("Consider we have","Rs 39").shift(2*UP).scale(0.75).set_color_by_tex_to_color_map({"Rs 39":[YELLOW,PURPLE]}) + text2=TextMobject("and we want to represent them only in terms of","Rs 2","and","Rs 5").shift(UP).scale(0.6).set_color_by_tex_to_color_map({"Rs 2":YELLOW,"Rs 5":PURPLE}) + text3=TextMobject("How many","Rs 2 coins","and","Rs 5 coins","do","we need?").scale(0.8).set_color_by_tex_to_color_map({"Rs 2 coins":YELLOW,"Rs 5 coins":PURPLE,"we need?":RED}) + text4=TextMobject("We","perform","the following!").scale(0.75).shift(DOWN).set_color_by_tex_to_color_map({"perform":GREEN}) + + self.play(FadeIn(text1)) + self.wait(0.6) + self.play(Write(text2)) + self.wait(0.5) + self.play(Write(text3)) + self.wait(0.7) + self.play(FadeIn(text4)) + self.wait(1) + self.play(FadeOut(text1),FadeOut(text2),FadeOut(text3),FadeOut(text4)) + + g1=self.group("Rs 39") + g1.shift(3*LEFT+0.75*UP) + l1=self.line() + l1.shift(4*LEFT) + f1=self.fiveGroup() + t1=self.twoGroup() + f1.shift(3.5*LEFT+0.7*DOWN) + andT=TextMobject("and").next_to(f1,buff=-0.1).scale(0.3) + t1.next_to(andT,buff=0.2) + equal1=TextMobject("$=$") + equal1.next_to(l1,buff=0.2) + + self.play(ShowCreation(g1)) + self.play(ShowCreation(l1)) + self.play(ShowCreation(f1),Write(andT),ShowCreation(t1)) + self.play(ShowCreation(equal1)) + self.wait(0.6) + + f2=self.fiveGroup().next_to(equal1,buff=0.4) + multiple1=TextMobject("$X7$","$\quad +$").next_to(f2,buff=0.2).set_color_by_tex_to_color_map({"$X7$":PURPLE}) + l2=self.line().next_to(multiple1,buff=0.4) + g2=self.group("Rs 4").shift(2.75*RIGHT+0.75*UP) + t2=self.twoGroup().shift(2.75*RIGHT+0.7*DOWN) + + self.play(ShowCreation(f2)) + self.play(ShowCreation(multiple1)) + self.play(ShowCreation(g2)) + self.play(ShowCreation(l2)) + self.play(ShowCreation(t2)) + self.wait(1) + + tempGrup=VGroup(g2,l2,t2) + + t3=self.twoGroup().next_to(multiple1,buff=0.4) + multiple2=TextMobject("$X2$").next_to(t3,buff=0.2).set_color_by_tex_to_color_map({"$X2$":YELLOW}) + + self.play(ReplacementTransform(tempGrup,t3)) + self.play(Write(multiple2)) + self.wait(2) + + def line(self): + l=Line(start=[0,0,0],end=[2,0,0]) + return l + + def twoGroup(self): + two=Circle(radius=0.25,color=BLACK,fill_color=YELLOW,fill_opacity=0.7) + twoText=TextMobject("Rs 2").scale(0.25).set_color(BLACK) + twoGrup=VGroup(two,twoText) + return twoGrup + + def fiveGroup(self): + five=Circle(radius=0.35,color=BLACK,fill_color=PURPLE,fill_opacity=0.7) + fiveText=TextMobject("Rs 5").scale(0.3).set_color(BLACK) + fiveGrup=VGroup(five,fiveText) + return fiveGrup + + def group(self,money): + coins=[ + Circle(radius=0.35,color=GREY,fill_color=GREY,fill_opacity=0.75), + Circle(radius=0.35,color=GREY,fill_color=GREY,fill_opacity=0.8), + Circle(radius=0.35,color=GREY,fill_color=GREY,fill_opacity=0.7), + Circle(radius=0.35,color=GREY,fill_color=GREY,fill_opacity=0.75), + Circle(radius=0.35,color=GREY,fill_color=GREY,fill_opacity=0.8), + Circle(radius=0.35,color=GREY,fill_color=GREY,fill_opacity=0.7) + ] + coinsText=TextMobject(money).set_color(BLACK) + coinsText.scale(0.35) + + coins[1].shift(0.2*RIGHT+0.2*UP) + coins[2].shift(0.2*RIGHT+0.1*DOWN) + coins[3].shift(0.2*DOWN) + coins[4].shift(0.2*UP+0.2*LEFT) + coins[5].shift(0.2*LEFT+0.1*LEFT) + + coinsGrup=VGroup(coins[0],coins[1],coins[2],coins[3],coins[4],coins[5],coinsText) + return coinsGrup + +class divideFunction(GraphScene): + CONFIG = { + "x_min": -6, + "x_max": 6, + "y_min": -300, + "y_max": 300, + "x_tick_frequency": 2, + "y_tick_frequency": 300, + "graph_origin": 3*LEFT+1.5*UP+6*LEFT, + "function_color": RED, + "axes_color": BLUE, + "x_axis_label": "$t$", + "y_axis_label": "$y$", + "x_labeled_nums": [-6,0,6], + "y_labeled_nums": [-300,0,300], + "x_axis_width": 1.5, + "y_axis_height": 1 + } + def line(self): + l=Line(start=[0,0,0],end=[2,0,0]) + return l + def construct(self): + text1=TextMobject("Similarly,").scale(0.8).shift(UP).set_color(RED) + text2=TextMobject("To find the amount of","each frequency","present in","$f(x)$").scale(0.6).set_color_by_tex_to_color_map({"each frequency":[YELLOW,RED],"$f(x)$":RED}) + text3=TextMobject("We","perform","the following!").scale(0.7).shift(DOWN).set_color_by_tex_to_color_map({"perform":GREEN}) + + self.play(FadeIn(text1)) + self.wait(0.6) + self.play(Write(text2)) + self.wait(0.7) + self.play(FadeIn(text3)) + + self.wait(1) + self.play(FadeOut(text1),FadeOut(text2),FadeOut(text3)) + + boxUP=Square(side_length=1.7,fill_color=BLUE_C,fill_opacity=0.5,color=BLACK).shift(3*LEFT+UP) + boxDOWN=Square(side_length=1.7,fill_color=BLUE_C,fill_opacity=0.5,color=BLACK).shift(3*LEFT+DOWN) + + axes=[] + self.graph_origin=10*LEFT+1.5*UP + self.setup_axes(scalee=1) + axes.append(self.axes) + fx=self.get_graph(lambda x:math.pow(x,3)-math.pow(x,2)+x-2,x_min=-2*math.pi,x_max=2*math.pi,color=RED).shift(7*RIGHT+0.5*DOWN) + + l=self.line().shift(4*LEFT) + + self.graph_origin=10*LEFT+1.5*DOWN + self.y_min=-2 + self.y_max=1 + self.y_tick_frequency=1 + self.y_labeled_nums=[-1,0,1] + self.setup_axes(scalee=1) + axes.append(self.axes) + sinx=self.get_graph(lambda x:np.sin(x),x_min=-2*math.pi,x_max=2*math.pi,color=PURPLE_C).shift(7*RIGHT+0.5*UP) + + equal=TextMobject("$=$").next_to(l,buff=0.3) + result1=TextMobject("Amount of").scale(0.6).next_to(equal,buff=0.3) + boxRIGHT=Square(side_length=1.7,fill_color=GOLD_B,fill_opacity=0.5,color=BLACK).next_to(result1,buff=0.2) + self.graph_origin=10*LEFT + sinxResult=self.get_graph(lambda x:np.sin(x),color=PURPLE_C).next_to(result1,buff=0.3) + axes.append(self.axes) + result2=TextMobject("in","$f(x)$").scale(0.6).next_to(sinxResult,buff=0.2).set_color_by_tex_to_color_map({"$f(x)$":RED}) + + self.play(FadeIn(boxUP)) + self.play(ShowCreation(fx)) + self.play(ShowCreation(l)) + self.play(FadeIn(boxDOWN)) + self.play(ShowCreation(sinx)) + self.wait(0.4) + self.play(Write(equal)) + self.play(Write(result1)) + self.play(FadeIn(boxRIGHT)) + self.play(ShowCreation(sinxResult)) + self.play(Write(result2)) + aText1=TextMobject("and").scale(0.65).shift(4*RIGHT+2*DOWN).set_color(GREEN) + self.play(Write(aText1)) + self.wait(0.7) + + self.graph_origin=10*LEFT + cos4x=self.get_graph(lambda x:np.cos(4*x),color=PURPLE_A).shift(7*RIGHT+0.5*UP) + axes.append(self.axes) + self.graph_origin=10*LEFT + cos4xResult=self.get_graph(lambda x:np.cos(4*x),color=PURPLE_A).next_to(result1,buff=0.3) + axes.append(self.axes) + self.play(ReplacementTransform(sinx,cos4x),ReplacementTransform(sinxResult,cos4xResult)) + self.wait(0.7) + + soText=TextMobject("And so on..!").scale(0.65).shift(4*RIGHT+2*DOWN).set_color(GREEN) + self.play(ReplacementTransform(aText1,soText)) + + self.graph_origin=10*LEFT + cosx=self.get_graph(lambda x:np.cos(x),color=GREEN_E).shift(7*RIGHT+0.5*UP) + axes.append(self.axes) + self.graph_origin=10*LEFT + cosxResult=self.get_graph(lambda x:np.cos(x),color=GREEN_E).next_to(result1,buff=0.3) + axes.append(self.axes) + self.play(ReplacementTransform(cos4x,cosx),ReplacementTransform(cos4xResult,cosxResult)) + + self.graph_origin=10*LEFT + cos3x=self.get_graph(lambda x:np.cos(3*x),color=GREEN_C).shift(7*RIGHT+0.5*UP) + axes.append(self.axes) + self.graph_origin=10*LEFT + cos3xResult=self.get_graph(lambda x:np.cos(3*x),color=GREEN_C).next_to(result1,buff=0.3) + axes.append(self.axes) + self.play(ReplacementTransform(cosx,cos3x),ReplacementTransform(cosxResult,cos3xResult)) + + self.graph_origin=10*LEFT + const=self.get_graph(lambda x:1,color=YELLOW_B).shift(7*RIGHT+0.5*UP) + axes.append(self.axes) + self.graph_origin=10*LEFT + constResult=self.get_graph(lambda x:1,color=YELLOW_B).next_to(result1,buff=0.3) + axes.append(self.axes) + self.play(ReplacementTransform(cos3x,const),ReplacementTransform(cos3xResult,constResult)) + + self.wait(1) + + self.play(FadeOut(soText),FadeOut(const),FadeOut(constResult),FadeOut(l),FadeOut(equal),FadeOut(result1),FadeOut(result2),FadeOut(fx),FadeOut(boxRIGHT),FadeOut(boxUP),FadeOut(boxDOWN)) + + finalFormula1=TexMobject(r"Therefore,",r"F(s)",r"=",r"\int _{ -\infty }^{ \infty }",r"{f(t)",r"\over",r"sines",r"\enspace and \enspace",r"cosines}",r"dt }").scale(0.7).set_color_by_tex_to_color_map({"F(s)":RED,"sines":BLUE,"cosines}":YELLOW,"{f(t)":GREEN}) + finalFormula2=TexMobject(r"F(s)",r"=",r"\int _{ -\infty }^{ \infty }",r"{f(t)",r"\over",r"{ e }^",r"{ i\theta }}",r"dt }").set_color_by_tex_to_color_map({"F(s)":RED,"{f(t)":GREEN}) + subFinalFormula=TextMobject("where","$\\theta =2\pi st$").scale(0.5).shift(DOWN+2*RIGHT).set_color_by_tex_to_color_map({"$\\theta =2\pi st$":RED}) + + self.play(Write(finalFormula1)) + self.wait(1) + self.play(ReplacementTransform(finalFormula1,finalFormula2)) + self.play(Write(subFinalFormula)) + self.wait(2) diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/README.md b/FSF-2020/calculus/series-and-transformations/Power Series/README.md index 85c6fc4..2fd400d 100644 --- a/FSF-2020/calculus/series-and-transformations/Power Series/README.md +++ b/FSF-2020/calculus/series-and-transformations/Power Series/README.md @@ -1,14 +1,14 @@ -#### PieChart - +#### Convergence Intuition + #### Convergence Intuition - + #### Convergence of a function - + #### Radius and IntervalOfConvergence - + #### Uniform Convergence - + diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file1_convergence_Intuition.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file1_convergence_Intuition.gif Binary files differnew file mode 100644 index 0000000..292d19d --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file1_convergence_Intuition.gif diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file1_pieChart.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file1_pieChart.gif Binary files differdeleted file mode 100644 index f102f6d..0000000 --- a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file1_pieChart.gif +++ /dev/null diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file1a_convergence_Intuition.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file1a_convergence_Intuition.gif Binary files differnew file mode 100644 index 0000000..287cbd1 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file1a_convergence_Intuition.gif diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file2_convergence_Intuition.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file2_convergence_Intuition.gif Binary files differdeleted file mode 100644 index 9463ac2..0000000 --- a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file2_convergence_Intuition.gif +++ /dev/null diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file2_convergence_of_a_function.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file2_convergence_of_a_function.gif Binary files differnew file mode 100644 index 0000000..78d6014 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file2_convergence_of_a_function.gif diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file3_convergence_of_a_function.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file3_convergence_of_a_function.gif Binary files differdeleted file mode 100644 index 836e044..0000000 --- a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file3_convergence_of_a_function.gif +++ /dev/null diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file3_radius_and_intervalOfConvergence.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file3_radius_and_intervalOfConvergence.gif Binary files differnew file mode 100644 index 0000000..a45c75e --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file3_radius_and_intervalOfConvergence.gif diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file4_UniformConvergence.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file4_UniformConvergence.gif Binary files differnew file mode 100644 index 0000000..7b635d7 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file4_UniformConvergence.gif diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file4_radius_and_intervalOfConvergence.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file4_radius_and_intervalOfConvergence.gif Binary files differdeleted file mode 100644 index e8dbff4..0000000 --- a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file4_radius_and_intervalOfConvergence.gif +++ /dev/null diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file4a_UniformConvergence.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file4a_UniformConvergence.gif Binary files differnew file mode 100644 index 0000000..e284b83 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file4a_UniformConvergence.gif diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file5_UniformConvergence.gif b/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file5_UniformConvergence.gif Binary files differdeleted file mode 100644 index 44cd78b..0000000 --- a/FSF-2020/calculus/series-and-transformations/Power Series/gifs/file5_UniformConvergence.gif +++ /dev/null diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/video2_convergence_Intuition.py b/FSF-2020/calculus/series-and-transformations/Power Series/video1_convergence_Intuition.py index 72356c6..66f48f9 100644 --- a/FSF-2020/calculus/series-and-transformations/Power Series/video2_convergence_Intuition.py +++ b/FSF-2020/calculus/series-and-transformations/Power Series/video1_convergence_Intuition.py @@ -11,23 +11,36 @@ class convergence(Scene): self.play(ApplyMethod(originalFormula.shift,2.7*UP)) self.wait(1) - terms=["$a_{ 0 }$","$a_{ 1 }x$","$a_{ 2 }x^{ 2 }$","$a_{ 3 }x^{ 3 }$","$a_{ 4 }x^{ 4 }$","$a_{ 5 }x^{ 5 }$","$a_{ 6 }x^{ 6 }$","$a_{ 7 }x^{ 7 }$","$a_{ 8 }x^{ 8 }$","$a_{ 9 }x^{ 9 }$","$a_{ 10 }x^{ 10 }$","$a_{ 11 }x^{ 11 }$"] + colors=[PURPLE_E,PURPLE_D,MAROON_D,RED_E,RED_D,RED_C,ORANGE,YELLOW_E,YELLOW_D,YELLOW_B] + terms=["$a_{ 0 }$","$a_{ 1 }x$","$a_{ 2 }x^{ 2 }$","$a_{ 3 }x^{ 3 }$","$a_{ 4 }x^{ 4 }$","$a_{ 5 }x^{ 5 }$","$a_{ 6 }x^{ 6 }$","$a_{ 7 }x^{ 7 }$","$a_{ 8 }x^{ 8 }$","$a_{ 9 }x^{ 9 }$"] termsTogetherString="+".join(terms) - termsTogether=TextMobject(termsTogetherString+"...") + #termsTogether=TextMobject(termsTogetherString+"...") + termsTogether=TextMobject("$a_{ 0 }$","+","$a_{ 1 }x$","+","$a_{ 2 }x^{ 2 }$","+","$a_{ 3 }x^{ 3 }$","+","$a_{ 4 }x^{ 4 }$","+","$a_{ 5 }x^{ 5 }$","+","$a_{ 6 }x^{ 6 }$","+","$a_{ 7 }x^{ 7 }$","+","$a_{ 8 }x^{ 8 }$","+","$a_{ 9 }x^{ 9 }$","+..") + termsTogether.set_color_by_tex_to_color_map({"$a_{ 0 }$":colors[0], + "$a_{ 1 }x$":colors[1], + "$a_{ 2 }x^{ 2 }$":colors[2], + "$a_{ 3 }x^{ 3 }$":colors[3], + "$a_{ 4 }x^{ 4 }$":colors[4], + "$a_{ 5 }x^{ 5 }$":colors[5], + "$a_{ 6 }x^{ 6 }$":colors[6], + "$a_{ 7 }x^{ 7 }$":colors[7], + "$a_{ 8 }x^{ 8 }$":colors[8], + "$a_{ 9 }x^{ 9 }$":colors[9]}) termsTogether.scale(0.8) termsTogether.shift(2.7*UP) self.play(ReplacementTransform(originalFormula,termsTogether)) self.wait(1) - termMobjectRect=[0]*12 - termMobject=TextMobject(terms[0]) + termMobjectRect=[0]*10 + termMobject=TextMobject(terms[0]).set_color(colors[0]) termMobject.shift(2.7*UP+6.2*LEFT) - for i in range(1,13): + for i in range(1,11): termMobjectOld=termMobject termMobjectOld.scale(0.8) - if(i<12): + if(i<10): termMobject=TextMobject(terms[i]) - termMobject.next_to(termMobjectOld) + termMobject.set_color(colors[i]) + termMobject.next_to(termMobjectOld,buff=0.5) if(i==1): rectDefine=TextMobject("Here","each rectangle","represents the","value of the term") rectDefine.set_color_by_tex_to_color_map({"each rectangle":BLUE,"value of the term":YELLOW}) @@ -50,7 +63,7 @@ class convergence(Scene): self.play(ReplacementTransform(ratio,inequality)) self.wait(1) #self.play(ApplyMethod(termMobjectOld.move_to,(2-0.3*i)*DOWN+RIGHT*0.2*i)) - termMobjectRect[i-1]=Rectangle(height=0.1,width=(5-0.4*i)) + termMobjectRect[i-1]=Rectangle(height=0.1,width=(4.2-0.4*i),color=colors[i-1]) termMobjectRect[i-1].move_to((2-0.2*i)*DOWN+RIGHT*0.2*i) #rectangles[p] = termMobjectRect #p+=1 @@ -58,8 +71,8 @@ class convergence(Scene): uparrow=TextMobject("$\\uparrow$") uparrow.set_color(GREEN) - uparrow.scale(6) - uparrow.shift(4*RIGHT+0.5*DOWN) + uparrow.scale(5) + uparrow.shift(4*RIGHT+0.7*DOWN) self.play(ShowCreation(uparrow)) self.wait(1) @@ -72,9 +85,9 @@ class convergence(Scene): self.play(FadeOut(converges),FadeOut(uparrow),FadeOut(inequality)) self.wait(0.5) - rect=VGroup(termMobjectRect[0],termMobjectRect[1],termMobjectRect[2],termMobjectRect[3],termMobjectRect[4],termMobjectRect[5],termMobjectRect[6],termMobjectRect[7],termMobjectRect[8],termMobjectRect[9],termMobjectRect[10],termMobjectRect[11]) + rect=VGroup(termMobjectRect[0],termMobjectRect[1],termMobjectRect[2],termMobjectRect[3],termMobjectRect[4],termMobjectRect[5],termMobjectRect[6],termMobjectRect[7],termMobjectRect[8],termMobjectRect[9]) self.play(ApplyMethod(rect.scale,0.2)) - for i in range(0,12): + for i in range(0,10): self.play(ApplyMethod(termMobjectRect[i].shift,i*0.04*DOWN+(11-(3-0.11*i)*i)*LEFT*0.3)) func=TextMobject("$\\approx$","$f(x)$") func.set_color_by_tex_to_color_map({"$f(x)$":RED}) diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/video1_pieChart.py b/FSF-2020/calculus/series-and-transformations/Power Series/video1_pieChart.py deleted file mode 100644 index 28eb07c..0000000 --- a/FSF-2020/calculus/series-and-transformations/Power Series/video1_pieChart.py +++ /dev/null @@ -1,128 +0,0 @@ -from manimlib.imports import * - - -def formFormula(coeff_list,variable_list): - coeff_list=[TextMobject("${ a }_{ 0 }$"),TextMobject("${ a }_{ 1 }$"),TextMobject("${ a }_{ 2 }$")] - variable_list=[TextMobject("+"),TextMobject("${ x }$+"),TextMobject("${ x }^{ 2 }$")] - coeff_list[0].shift(2.2*UP+1.6*LEFT) - for i in range(0,3): - coeff_list[i].set_color(GOLD_A) - variable_list[i].next_to(coeff_list[i],buff=0.1) - if i!=2: - coeff_list[i+1].next_to(variable_list[i],buff=0.1) - dots=TextMobject("...") - dots.next_to(variable_list[2]) - expansion=VGroup(coeff_list[0],coeff_list[1],coeff_list[2],variable_list[0],variable_list[1],variable_list[2],dots) - expansion.scale(0.7) - return expansion - -class pieChart(Scene): - def construct(self): - circle1=Circle(radius=3,color=BLUE) - powerText=TextMobject("Power Series") - powerText.scale(0.8) - self.play(FadeIn(powerText)) - self.play(ShowCreation(circle1)) - self.wait(1) - - powerGroup=VGroup(circle1,powerText) - - self.play(ApplyMethod(powerGroup.scale,0.5)) - self.play(ApplyMethod(powerGroup.move_to,2.2*UP)) - self.wait(0.5) - expansion_power_coeff=[] - variables_power=[] - expansion_power=formFormula(expansion_power_coeff,variables_power) - self.play(ReplacementTransform(powerText,expansion_power)) - self.wait(1) - - circle2=Circle(radius=1.5) - circle2.shift(2.2*UP) - expansion_geo_coeff=[0]*3 - variables_geo=[0]*3 - arrow1_2=Line(start=0.7*UP,end=2.5*LEFT) - expansion_geo_coeff=[TextMobject("${ a }_{ 0 }$"),TextMobject("${ a }_{ 1 }$"),TextMobject("${ a }_{ 2 }$")] - for i in range(0,3): - expansion_geo_coeff[i].set_color(GOLD_A) - variables_geo=[TextMobject("+"),TextMobject("${ x }$+"),TextMobject("${ x }^{ 2 }$")] - expansion_geo_coeff[0].shift(2.2*UP+1.6*LEFT) - for i in range(0,3): - variables_geo[i].next_to(expansion_geo_coeff[i],buff=0.1) - if i!=2: - expansion_geo_coeff[i+1].next_to(variables_geo[i],buff=0.1) - dots=TextMobject("...") - dots.next_to(variables_geo[2]) - expansion_geo=VGroup(expansion_geo_coeff[0],expansion_geo_coeff[1],expansion_geo_coeff[2],variables_geo[0],variables_geo[1],variables_geo[2],dots) - expansion_geo.scale(0.7) - - self.play(ApplyMethod(circle2.shift,4*LEFT+2.5*DOWN),ApplyMethod(expansion_geo.shift,4*LEFT+2.5*DOWN)) - self.add(arrow1_2) - self.wait(1) - - ones=[TextMobject("1"),TextMobject("1"),TextMobject("1")] - for i in range(0,3): - ones[i].set_color(GOLD_A) - ones[0].shift(0.3*DOWN,5*LEFT) - ones[1].next_to(ones[0],buff=0.5) - ones[2].next_to(ones[1],buff=0.7) - self.play(ReplacementTransform(expansion_geo_coeff[0],ones[0]),ReplacementTransform(expansion_geo_coeff[1],ones[1]),ReplacementTransform(expansion_geo_coeff[2],ones[2])) - self.wait(1) - expansion_geo=VGroup(ones[0],ones[1],ones[2],variables_geo[0],variables_geo[1],variables_geo[2],dots) - - expansion_geo_final=TextMobject("$1+x+{ x }^{ 2 }..$") - expansion_geo_final.scale(0.8) - expansion_geo_final.shift(0.3*DOWN+4*LEFT) - self.play(ReplacementTransform(expansion_geo,expansion_geo_final)) - self.wait(1) - - circle3=Circle(radius=1.5,color=GREEN) - circle3.shift(2.2*UP) - expansion_taylor_coeff=[0]*3 - variables_taylor=[0]*3 - arrow1_3=Line(start=0.7*UP,end=DOWN*0.3) - expansion_taylor_coeff=[TextMobject("${ a }_{ 0 }$"),TextMobject("${ a }_{ 1 }$"),TextMobject("${ a }_{ 2 }$")] - for i in range(0,3): - expansion_taylor_coeff[i].set_color(GOLD_A) - variables_taylor=[TextMobject("+"),TextMobject("${ x }$+"),TextMobject("${ x }^{ 2 }$")] - expansion_taylor_coeff[0].shift(2.2*UP+1.6*LEFT) - for i in range(0,3): - variables_taylor[i].next_to(expansion_taylor_coeff[i],buff=0.1) - if i!=2: - expansion_taylor_coeff[i+1].next_to(variables_taylor[i],buff=0.1) - dots=TextMobject("...") - dots.next_to(variables_taylor[2]) - expansion_taylor=VGroup(expansion_taylor_coeff[0],expansion_taylor_coeff[1],expansion_taylor_coeff[2],variables_taylor[0],variables_taylor[1],variables_taylor[2],dots) - expansion_taylor.scale(0.7) - - self.play(ApplyMethod(circle3.shift,4*DOWN),ApplyMethod(expansion_taylor.shift,4*DOWN)) - self.add(arrow1_3) - self.wait(1) - - differentials=[TextMobject("$f(0)$"),TextMobject("${ f'\left( 0 \\right) }$"),TextMobject("$\\frac { f''\left( 0 \\right) }{ 2! }$")] - for i in range(0,3): - differentials[i].set_color(GOLD_A) - differentials[0].shift(1.8*DOWN+1.15*LEFT) - differentials[1].shift(1.8*DOWN+0.45*LEFT) - differentials[2].shift(1.8*DOWN+0.45*RIGHT) - differentials[0].scale(0.35) - differentials[1].scale(0.35) - differentials[2].scale(0.35) - self.play(ReplacementTransform(expansion_taylor_coeff[0],differentials[0]),ReplacementTransform(expansion_taylor_coeff[1],differentials[1]),ReplacementTransform(expansion_taylor_coeff[2],differentials[2])) - self.wait(2) - expansion_taylor_final=VGroup(differentials[0],differentials[1],differentials[2],variables_taylor[0],variables_taylor[1],variables_taylor[2],dots) - - self.play(FadeOut(expansion_geo_final),FadeOut(expansion_taylor_final)) - geoText=TextMobject("Geometric Series") - geoText.scale(0.7) - geoText.shift(4*LEFT+0.3*DOWN) - taylorText=TextMobject("Taylor Series") - taylorText.scale(0.7) - taylorText.shift(1.8*DOWN) - self.play(FadeIn(geoText),FadeIn(taylorText)) - self.wait(1) - - soOntext=TextMobject("So on..!") - soOntext.shift(4*RIGHT) - soOntext.scale(0.8) - self.play(FadeIn(soOntext)) - self.wait(2) diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/video3_convergence_of_a_function.py b/FSF-2020/calculus/series-and-transformations/Power Series/video2_convergence_of_a_function.py index f710f42..19b8b8b 100644 --- a/FSF-2020/calculus/series-and-transformations/Power Series/video3_convergence_of_a_function.py +++ b/FSF-2020/calculus/series-and-transformations/Power Series/video2_convergence_of_a_function.py @@ -69,10 +69,10 @@ class graphScene(GraphScene): eqText[i].scale(0.6) eqText[i].set_color(BLUE) eqText[i].shift(ORIGIN+UP*2*y_each_unit+RIGHT*3.3*x_each_unit) - eqTextTerm=TextMobject("And so on..!") - eqTextTerm.set_color(BLUE) - eqTextTerm.scale(0.6) - eqTextTerm.shift(ORIGIN+UP*2*y_each_unit+3*RIGHT*x_each_unit) + # eqTextTerm=TextMobject("And so on..!") + # eqTextTerm.set_color(BLUE) + # eqTextTerm.scale(0.6) + # eqTextTerm.shift(ORIGIN+UP*2*y_each_unit+3*RIGHT*x_each_unit) equation1 = self.get_graph(lambda x : 1,color = RED,x_min = -8,x_max=8) equation2 = self.get_graph(lambda x : 1-math.pow(x,2),color = RED,x_min = -1.7,x_max=1.7) equation3 = self.get_graph(lambda x : 1-math.pow(x,2)+math.pow(x,4),color = RED,x_min = -1.6,x_max=1.6) @@ -106,7 +106,7 @@ class graphScene(GraphScene): self.play(ReplacementTransform(equation3,equation4),ReplacementTransform(eqText[2],eqText[3])) self.wait(0.3) self.play(FadeOut(eqText[3])) - self.play(FadeIn(eqTextTerm)) + #self.play(FadeIn(eqTextTerm)) self.play(Write(textBtwAnim1),Write(textBtwAnim2)) self.play(FadeIn(textBtwAnim3)) self.play(ReplacementTransform(equation4,equation5)) @@ -122,7 +122,7 @@ class graphScene(GraphScene): self.play(ReplacementTransform(equation9,equation10)) self.wait(1) - self.play(FadeOut(textBtwAnim1),FadeOut(textBtwAnim2),FadeOut(textBtwAnim3),FadeOut(equation10),FadeOut(eqTextTerm)) + self.play(FadeOut(textBtwAnim1),FadeOut(textBtwAnim2),FadeOut(textBtwAnim3),FadeOut(equation10)) self.wait(1) convergeLine=Line(start=ORIGIN+x_each_unit*LEFT,end=ORIGIN+x_each_unit*RIGHT,color=WHITE) diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/video4_radius_and_intervalOfConvergence.py b/FSF-2020/calculus/series-and-transformations/Power Series/video3_radius_and_intervalOfConvergence.py index 412d20c..f35fea8 100644 --- a/FSF-2020/calculus/series-and-transformations/Power Series/video4_radius_and_intervalOfConvergence.py +++ b/FSF-2020/calculus/series-and-transformations/Power Series/video3_radius_and_intervalOfConvergence.py @@ -3,7 +3,7 @@ import math class intro(Scene): def construct(self): - introText1=TextMobject("Consider the","above","example..") + introText1=TextMobject("Consider the example","above",) introText1.scale(0.8) introText1.set_color_by_tex_to_color_map({"above":YELLOW}) self.play(Write(introText1)) @@ -24,12 +24,13 @@ class graphScene(GraphScene,MovingCameraScene): "x_labeled_nums": range(-1, 2, 1), "y_labeled_nums": range(0,2,1), "y_axis_height":7, - "x_axis_width":7 + "x_axis_width":7, } def setup(self): GraphScene.setup(self) MovingCameraScene.setup(self) + def construct(self): x_each_unit = self.x_axis_width / (self.x_max - self.x_min) @@ -74,15 +75,14 @@ class graphScene(GraphScene,MovingCameraScene): radiusText=TextMobject("Radius of convergence") radiusText.scale(0.14) radiusText.shift(ORIGIN+RIGHT*x_each_unit*0.45+DOWN*y_each_unit*0.2) - + #self.activate_zooming(animate=True) self.play(Write(radiusText)) self.wait(0.6) self.camera_frame.save_state() - self.camera_frame.set_width(5.5) - self.play(self.camera_frame.move_to, ORIGIN) + self.play(self.camera_frame.set_width,5.5) self.wait(1) - self.camera_frame.set_width(14) + self.play(self.camera_frame.set_width,14) self.wait(1.3) self.play(FadeOut(radiusText),FadeOut(circle),FadeOut(movingPoint)) @@ -101,8 +101,13 @@ class graphScene(GraphScene,MovingCameraScene): self.wait(0.6) self.camera_frame.save_state() - self.camera_frame.set_width(5.5) - self.play(self.camera_frame.move_to, ORIGIN) + self.play(self.camera_frame.set_width,5.5) self.wait(1) - self.camera_frame.set_width(14) - self.wait(1.5) + self.play(self.camera_frame.set_width,14) + self.wait(1.3) + # self.camera_frame.save_state() + # self.camera_frame.set_width(5.5) + # self.play(self.camera_frame.move_to, ORIGIN) + # self.wait(1) + # self.camera_frame.set_width(14) + # self.wait(1.5) diff --git a/FSF-2020/calculus/series-and-transformations/Power Series/video5_UniformConvergence.py b/FSF-2020/calculus/series-and-transformations/Power Series/video4_UniformConvergence.py index e9681aa..1f3e26c 100644 --- a/FSF-2020/calculus/series-and-transformations/Power Series/video5_UniformConvergence.py +++ b/FSF-2020/calculus/series-and-transformations/Power Series/video4_UniformConvergence.py @@ -3,19 +3,19 @@ import math class uniformlyConvergent(Scene): def construct(self): - introText1=TextMobject("Again consider the","above","example") + #introText1=TextMobject("Again consider the","above","example") introText2=TextMobject("Let","$g(x)=\\frac { 1 }{ 1+{ x }^{ 2 } }$","and","x=0.5 $\in$(-1,1)") introText3=TextMobject("Lets analyse..","!") - introText1.scale(0.8) + #introText1.scale(0.8) introText2.scale(0.7) introText3.scale(0.9) introText3.shift(DOWN) - introText1.set_color_by_tex_to_color_map({"above":YELLOW}) + #introText1.set_color_by_tex_to_color_map({"above":YELLOW}) introText2.set_color_by_tex_to_color_map({"$g(x)=\\frac { 1 }{ 1+{ x }^{ 2 } }$":BLUE,"x=0.5 $\in$(-1,1)":YELLOW}) introText3.set_color_by_tex_to_color_map({"!":GREEN}) - self.play(Write(introText1)) - self.wait(0.5) - self.play(FadeOut(introText1)) + #self.play(Write(introText1)) + #self.wait(0.5) + #self.play(FadeOut(introText1)) self.play(Write(introText2)) self.play(FadeIn(introText3)) self.wait(2) @@ -45,7 +45,7 @@ def makeLines(x,numPoints,x_each_unit,y_each_unit): lines[i]=Line(start=ORIGIN+RIGHT*x_each_unit*i+UP*y_each_unit*y,end=ORIGIN+RIGHT*x_each_unit*(i+1)+UP*y_each_unit*y_next,color=RED) return lines -class graphScene(GraphScene,MovingCameraScene): +class graphScene(GraphScene,ZoomedScene): CONFIG = { "x_min": -6, "x_max": 6, @@ -58,12 +58,15 @@ class graphScene(GraphScene,MovingCameraScene): "y_axis_label": "$f(\\frac{1}{2})_k$", "exclude_zero_label": True, "x_axis_width":7, - "y_axis_height":7 + "y_axis_height":7, + "zoomed_camera_frame_starting_position": 0.5*UP+0.5*RIGHT, + "zoom_factor": 0.4, } def setup(self): GraphScene.setup(self) - MovingCameraScene.setup(self) + #MovingCameraScene.setup(self) + ZoomedScene.setup(self) def construct(self): @@ -87,6 +90,14 @@ class graphScene(GraphScene,MovingCameraScene): makeSeries(0.5,points,x_each_unit,y_each_unit) lines=makeLines(0.5,6,x_each_unit,y_each_unit) + func1=TextMobject("$g(x)=\\frac { 1 }{ 1+{ x }^{ 2 } }$") + func2=TextMobject("x=0.5 $\in$(-1,1)") + func1.scale(0.4) + func2.scale(0.4) + func1.shift(5.3*LEFT+3.3*UP) + func2.shift(5.3*LEFT+2.9*UP) + self.add(func1) + self.add(func2) self.add(sequence) self.add(formula) @@ -95,22 +106,26 @@ class graphScene(GraphScene,MovingCameraScene): self.add(fLineText) for p in points: self.add(p) + self.setup() + self.activate_zooming(animate=True) for p in range(0,5): self.play(Write(lines[p])) - self.wait(0.5) - self.camera_frame.save_state() - self.camera_frame.set_width(0.6) - self.play(self.camera_frame.move_to, points[0]) - self.wait(0.4) - self.play(self.camera_frame.move_to, points[1]) - self.wait(0.4) - self.play(self.camera_frame.move_to, points[2]) - self.wait(0.3) - self.play(self.camera_frame.move_to, points[3]) - self.wait(1) - self.play(self.camera_frame.move_to,ORIGIN) - self.camera_frame.set_width(14) + # self.wait(0.5) + # self.camera_frame.save_state() + # self.camera_frame.set_width(0.6) + # self.play(self.camera_frame.move_to, points[0]) + # self.wait(0.4) + # self.play(self.camera_frame.move_to, points[1]) + # self.wait(0.4) + # self.play(self.camera_frame.move_to, points[2]) + # self.wait(0.3) + # self.play(self.camera_frame.move_to, points[3]) + # self.wait(1) + # self.play(self.camera_frame.move_to,ORIGIN) + # self.camera_frame.set_width(14) + self.wait(1) + self.get_zoomed_display_pop_out_animation() explanation1=TextMobject("Since the series","converges","to") explanation1.set_color_by_tex_to_color_map({"converges":YELLOW}) diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/README.md b/FSF-2020/calculus/series-and-transformations/Taylor Series/README.md index ce3b088..88eb772 100644 --- a/FSF-2020/calculus/series-and-transformations/Taylor Series/README.md +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/README.md @@ -2,7 +2,7 @@  #### Taylor Series GeneralForm - + #### Radius Of Convergence  diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file1_Example_TaylorExpansion.gif b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file1_Example_TaylorExpansion.gif Binary files differindex ecd3272..4272d84 100644 --- a/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file1_Example_TaylorExpansion.gif +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file1_Example_TaylorExpansion.gif diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file2_TaylorExpansionGeneralForm.gif b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file2_TaylorExpansionGeneralForm.gif Binary files differindex e6d9171..33dfa81 100644 --- a/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file2_TaylorExpansionGeneralForm.gif +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file2_TaylorExpansionGeneralForm.gif diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file2a_TaylorExpansionGeneralForm.gif b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file2a_TaylorExpansionGeneralForm.gif Binary files differnew file mode 100644 index 0000000..33dfa81 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file2a_TaylorExpansionGeneralForm.gif diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file3_radiusOfConvergence.gif b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file3_radiusOfConvergence.gif Binary files differindex 6b22d8d..9e53cfb 100644 --- a/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file3_radiusOfConvergence.gif +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file3_radiusOfConvergence.gif diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file4_DivergentRemainder.gif b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file4_DivergentRemainder.gif Binary files differindex 2bb5185..0bc8b65 100644 --- a/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file4_DivergentRemainder.gif +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/gifs/file4_DivergentRemainder.gif diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/video1_Example_TaylorExpansion.py b/FSF-2020/calculus/series-and-transformations/Taylor Series/video1_Example_TaylorExpansion.py index e83eff8..b132811 100644 --- a/FSF-2020/calculus/series-and-transformations/Taylor Series/video1_Example_TaylorExpansion.py +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/video1_Example_TaylorExpansion.py @@ -31,7 +31,7 @@ class intro(Scene): self.wait(0.7) self.play(FadeOut(equation),FadeOut(text)) -class graphScene(GraphScene): +class graphScene(GraphScene,MovingCameraScene): CONFIG = { "x_min": -8, "x_max": 8, @@ -45,10 +45,25 @@ class graphScene(GraphScene): "exclude_zero_label": True, "x_labeled_nums": range(-8, 8, 1), } + def setup(self): + GraphScene.setup(self) + MovingCameraScene.setup(self) def construct(self): x_each_unit = self.x_axis_width / (self.x_max - self.x_min) y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + equation=TextMobject("$f(x)=$","${ e }^{ -x^{ 2 } }$") + equation.scale(0.55) + equation.set_color_by_tex_to_color_map({"${ e }^{ -x^{ 2 } }$":RED}) + text=TextMobject("$a=0$") + text.scale(0.55) + + equation.shift(3.39*UP+5*LEFT) + text.shift(2.9*UP+5*LEFT) + + self.add(equation) + self.add(text) + generalized_eq_coeff=[] variables_eq=[] eq,generalized_eq_coeff=formFormula(generalized_eq_coeff,variables_eq) @@ -58,7 +73,7 @@ class graphScene(GraphScene): trTextGrup.scale(0.5) trTextGrup.to_corner(UP+RIGHT) self.play(Write(trTextGrup)) - self.setup_axes(animate=True) + self.setup_axes(animate=True,scalee=1) fx=TextMobject("${ e }^{ -x^{ 2 } }$") fx.scale(0.5) @@ -66,18 +81,21 @@ class graphScene(GraphScene): mainfunction=self.get_graph(lambda x:math.exp(-1*pow(x,2)),color=RED,x_min=-8,x_max=8) self.play(ShowCreation(mainfunction)) self.play(FadeIn(fx)) - self.wait(1.4) + self.wait(1) coeff=[TextMobject("$1$"),TextMobject("$f'(x)$"),TextMobject("$\\frac { f''(x) }{ 2! } $")] coeff[0].shift(3.39*UP+4.88*RIGHT) coeff[0].scale(0.5) - coeff[1].shift(3.39*UP+5.3*RIGHT) + coeff[1].shift(3.39*UP+5.4*RIGHT) coeff[1].scale(0.275) - coeff[2].shift(3.39*UP+5.98*RIGHT) + coeff[2].shift(3.39*UP+6*RIGHT) coeff[2].scale(0.28) for obj in coeff: obj.set_color(GOLD_A) + group=VGroup(coeff[0],coeff[1],coeff[2]) + + #group.shift(2*LEFT+2*DOWN) firstApprox=[self.get_graph(lambda x:1,color=BLUE)] secondApprox=[self.get_graph(lambda x:1,color=BLUE), @@ -124,16 +142,44 @@ class graphScene(GraphScene): bottomText8.scale(0.5) bottomText1.shift(4.5*RIGHT+2.5*DOWN) - bottomText2.shift(4.5*RIGHT+2.5*DOWN) - bottomText3.shift(4.5*RIGHT+2.5*DOWN) - bottomText4.shift(4.5*RIGHT+2.5*DOWN) - bottomText5.shift(4.5*RIGHT+2.5*DOWN) - bottomText6.shift(4.5*RIGHT+2.5*DOWN) - bottomText7.shift(4.5*RIGHT+2.5*DOWN) - bottomText8.shift(4.5*RIGHT+2.5*DOWN) + # bottomText2.shift(4.5*RIGHT+2.5*DOWN) + # bottomText3.shift(4.5*RIGHT+2.5*DOWN) + # bottomText4.shift(4.5*RIGHT+2.5*DOWN) + # bottomText5.shift(4.5*RIGHT+2.5*DOWN) + # bottomText6.shift(4.5*RIGHT+2.5*DOWN) + # bottomText7.shift(4.5*RIGHT+2.5*DOWN) + # bottomText8.shift(4.5*RIGHT+2.5*DOWN) + bottomText2.shift(3*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText3.shift(3*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText4.shift(3*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText5.shift(3*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText6.shift(3.7*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText7.shift(3.7*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText8.shift(3.7*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + + bottomText2.scale(0.7) + bottomText3.scale(0.7) + bottomText4.scale(0.7) + bottomText5.scale(0.7) + bottomText6.scale(0.7) + bottomText7.scale(0.7) + bottomText8.scale(0.7) self.play(Write(bottomText1)) - self.wait(1) + self.wait(0.8) + #self.activate_zooming(animate=True) + self.camera_frame.save_state() + group.move_to(4*y_each_unit*UP+4.6*RIGHT*x_each_unit).scale(0.7) + self.play(self.camera_frame.set_width, 8, + self.camera_frame.move_to, x_each_unit*UP, + ApplyMethod(trTextGrup.move_to,4*y_each_unit*UP+4.1*RIGHT*x_each_unit), + ApplyMethod(bottomText1.move_to,3.4*RIGHT*x_each_unit+2.5*DOWN*y_each_unit), + ApplyMethod(equation.shift,1.39*DOWN+2*RIGHT), + ApplyMethod(text.shift,1.39*DOWN+2*RIGHT),) + self.play(ApplyMethod(text.scale,0.5),ApplyMethod(equation.scale,0.5),ApplyMethod(bottomText1.scale,0.6),ApplyMethod(trTextGrup.scale,0.7)) + self.play(ApplyMethod(text.shift,0.3*UP)) + self.wait(0.6) + self.play(ShowCreation(firstApprox[0]),ReplacementTransform(bottomText1,bottomText2)) #change coeff in tn(x) self.play(ReplacementTransform(generalized_eq_coeff[0],coeff[0])) @@ -170,10 +216,12 @@ class graphScene(GraphScene): self.wait(2) textFinal=TextMobject("And so on..!") - textFinal.scale(0.7) - textFinal.shift(4.5*RIGHT+2.5*DOWN) + textFinal.scale(0.35) + textFinal.shift(3.7*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) self.play(ReplacementTransform(bottomText8,textFinal)) - self.wait(2.5) + self.wait(1) + self.play(FadeOut(equation),FadeOut(text)) + self.play(self.camera_frame.set_width, 15) finalFormula=TextMobject("Hence","$T_{ n }(x)$","=","$f(0)+f'(0)x+\\frac { f''(0) }{ 2! }x^2+..+\\frac { { f }^{ n }(0) }{ n! } { x }^{ n }$") finalFormula.scale(0.8) diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/video2_TaylorExpansionGeneralForm.py b/FSF-2020/calculus/series-and-transformations/Taylor Series/video2_TaylorExpansionGeneralForm.py index f84cfe9..75f200d 100644 --- a/FSF-2020/calculus/series-and-transformations/Taylor Series/video2_TaylorExpansionGeneralForm.py +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/video2_TaylorExpansionGeneralForm.py @@ -7,7 +7,7 @@ class intro(Scene): equation=TextMobject("$f(x)=$","${ e }^{ -x^{ 2 } }$") equation.scale(2) equation.set_color_by_tex_to_color_map({"${ e }^{ -x^{ 2 } }$":RED}) - text=TextMobject("at $a=1$") + text=TextMobject("about $x=1$") text.scale(0.7) text.shift(DOWN) @@ -41,7 +41,7 @@ def formFormula(coeff_list,variable_list): return expansion,coeff_list -class graphScene(GraphScene): +class graphScene(GraphScene,MovingCameraScene): CONFIG = { "x_min": -8, "x_max": 8, @@ -55,10 +55,25 @@ class graphScene(GraphScene): "exclude_zero_label": True, "x_labeled_nums": range(-8, 8, 1), } + def setup(self): + GraphScene.setup(self) + MovingCameraScene.setup(self) def construct(self): x_each_unit = self.x_axis_width / (self.x_max - self.x_min) y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + equation=TextMobject("$f(x)=$","${ e }^{ -x^{ 2 } }$") + equation.scale(0.55) + equation.set_color_by_tex_to_color_map({"${ e }^{ -x^{ 2 } }$":RED}) + text=TextMobject("about $x=1$") + text.scale(0.55) + equation.shift(3.39*UP+5*LEFT) + text.shift(3*UP+5*LEFT) + + self.add(equation) + self.add(text) + + generalized_eq_coeff=[] variables_eq=[] eq,generalized_eq_coeff=formFormula(generalized_eq_coeff,variables_eq) @@ -68,7 +83,7 @@ class graphScene(GraphScene): trTextGrup.scale(0.5) trTextGrup.to_corner(UP+RIGHT) self.play(Write(trTextGrup)) - self.setup_axes(animate=True) + self.setup_axes(animate=True,scalee=1) fx=TextMobject("${ e }^{ -x^{ 2 } }$") fx.scale(0.5) @@ -79,29 +94,29 @@ class graphScene(GraphScene): self.wait(1.4) coeff=[TextMobject("$e^{-1}$"),TextMobject("$f'(x)$"),TextMobject("$\\frac { f''(x) }{ 2! } $")] - coeff[0].shift(3.33*UP+3.65*RIGHT) - coeff[0].scale(0.45) - coeff[1].shift(3.33*UP+4.13*RIGHT) - coeff[1].scale(0.275) - coeff[2].shift(3.33*UP+5.36*RIGHT) - coeff[2].scale(0.28) + coeff[0].shift(4.1*y_each_unit*UP+5.15*RIGHT*x_each_unit) + coeff[0].scale(0.3) + coeff[1].shift(4*y_each_unit*UP+5.7*RIGHT*x_each_unit) + coeff[1].scale(0.2) + coeff[2].shift(4*y_each_unit*UP+7.3*RIGHT*x_each_unit) + coeff[2].scale(0.18) for obj in coeff: obj.set_color(GOLD_A) - firstApprox=[self.get_graph(lambda x:math.exp(-1),color=BLUE,x_min=-5.5,x_max=5.5)] - secondApprox=[self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1),color=BLUE,x_min=-5.5,x_max=5.5), - self.get_graph(lambda x:math.exp(-1)+3*(x-1)*math.exp(-1),color=BLUE,x_min=-5.5,x_max=5.5), - self.get_graph(lambda x:math.exp(-1)-4*(x-1)*math.exp(-1),color=BLUE,x_min=-5.5,x_max=5.5)] - thirdApprox=[self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)-2*math.exp(-1)*(x-1)**2,color=BLUE,x_max=5.5,x_min=-5.5), - self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)-0.1*math.exp(-1)*(x-1)**2,color=BLUE,x_max=5.5,x_min=-5.5), - self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1),color=BLUE,x_max=5.5,x_min=-5.5), - self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)+0.5*math.exp(-1)*(x-1)**2,color=BLUE,x_max=5.5,x_min=-5.5), - self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)+2*math.exp(-1)*(x-1)**2,color=BLUE,x_max=5.5,x_min=-5.5)] + firstApprox=[self.get_graph(lambda x:math.exp(-1),color=BLUE,x_min=-3,x_max=4)] + secondApprox=[self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1),color=BLUE,x_min=-3,x_max=4), + self.get_graph(lambda x:math.exp(-1)+3*(x-1)*math.exp(-1),color=BLUE,x_min=-3,x_max=4), + self.get_graph(lambda x:math.exp(-1)-4*(x-1)*math.exp(-1),color=BLUE,x_min=-3,x_max=4)] + thirdApprox=[self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)-2*math.exp(-1)*(x-1)**2,color=BLUE,x_max=4,x_min=-3), + self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)-0.1*math.exp(-1)*(x-1)**2,color=BLUE,x_max=4,x_min=-3), + self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1),color=BLUE,x_max=4,x_min=-3), + self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)+0.5*math.exp(-1)*(x-1)**2,color=BLUE,x_max=4,x_min=-3), + self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)+2*math.exp(-1)*(x-1)**2,color=BLUE,x_max=4,x_min=-3)] - firstGraph=self.get_graph(lambda x:math.exp(-1),color=BLUE,x_min=-5.5,x_max=5.5) - secondGraph=self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1),color=BLUE,x_min=-5.5,x_max=5.5) - thirdGraph=self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)+math.exp(-1)*(x-1)**2,color=BLUE,x_max=5.5,x_min=-5.5) + firstGraph=self.get_graph(lambda x:math.exp(-1),color=BLUE,x_min=-3,x_max=4) + secondGraph=self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1),color=BLUE,x_min=-3,x_max=4) + thirdGraph=self.get_graph(lambda x:math.exp(-1)-2*(x-1)*math.exp(-1)+math.exp(-1)*(x-1)**2,color=BLUE,x_max=4,x_min=-3) bottomText1=TextMobject("Apply","$f(1)=T_{n}(1)$") bottomText2=TextMobject("This gives","$a_{ 0 }=e^{-1}$") @@ -135,16 +150,42 @@ class graphScene(GraphScene): bottomText8.scale(0.5) bottomText1.shift(4.5*RIGHT+2.5*DOWN) - bottomText2.shift(4.5*RIGHT+2.5*DOWN) - bottomText3.shift(4.5*RIGHT+2.5*DOWN) - bottomText4.shift(4.5*RIGHT+2.5*DOWN) - bottomText5.shift(4.5*RIGHT+2.5*DOWN) - bottomText6.shift(4.5*RIGHT+2.5*DOWN) - bottomText7.shift(4.5*RIGHT+2.5*DOWN) - bottomText8.shift(4.5*RIGHT+2.5*DOWN) + # bottomText2.shift(4.5*RIGHT+2.5*DOWN) + # bottomText3.shift(4.5*RIGHT+2.5*DOWN) + # bottomText4.shift(4.5*RIGHT+2.5*DOWN) + # bottomText5.shift(4.5*RIGHT+2.5*DOWN) + # bottomText6.shift(4.5*RIGHT+2.5*DOWN) + # bottomText7.shift(4.5*RIGHT+2.5*DOWN) + # bottomText8.shift(4.5*RIGHT+2.5*DOWN) + bottomText2.shift(5*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText3.shift(5*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText4.shift(5*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText5.shift(5*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText6.shift(5.7*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText7.shift(5.7*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + bottomText8.shift(5.7*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) + + bottomText2.scale(0.7) + bottomText3.scale(0.7) + bottomText4.scale(0.7) + bottomText5.scale(0.7) + bottomText6.scale(0.7) + bottomText7.scale(0.7) + bottomText8.scale(0.7) self.play(Write(bottomText1)) - self.wait(1) + self.wait(0.8) + self.camera_frame.save_state() + self.play(self.camera_frame.set_width, 8, + self.camera_frame.move_to, x_each_unit*UP+x_each_unit*2*RIGHT, + ApplyMethod(trTextGrup.move_to,4*y_each_unit*UP+6.1*RIGHT*x_each_unit), + ApplyMethod(bottomText1.move_to,5.4*RIGHT*x_each_unit+2.5*DOWN*y_each_unit), + ApplyMethod(equation.shift,1.39*DOWN+2*RIGHT+RIGHT*x_each_unit*2), + ApplyMethod(text.shift,1.39*DOWN+2*RIGHT+RIGHT*x_each_unit*2),) + self.play(ApplyMethod(text.scale,0.5),ApplyMethod(equation.scale,0.5),ApplyMethod(bottomText1.scale,0.6),ApplyMethod(trTextGrup.scale,0.7)) + self.play(ApplyMethod(text.shift,0.25*UP)) + self.wait(0.6) + self.play(ShowCreation(firstApprox[0]),ReplacementTransform(bottomText1,bottomText2)) #change coeff in tn(x) self.play(ReplacementTransform(generalized_eq_coeff[0],coeff[0])) @@ -181,10 +222,13 @@ class graphScene(GraphScene): self.wait(2) textFinal=TextMobject("And so on..!") - textFinal.scale(0.7) - textFinal.shift(4.5*RIGHT+2.5*DOWN) + textFinal.scale(0.35) + textFinal.shift(5.7*RIGHT*x_each_unit+2.5*DOWN*y_each_unit) self.play(ReplacementTransform(bottomText8,textFinal)) - self.wait(2.5) + self.wait(1) + self.play(FadeOut(equation),FadeOut(text)) + self.play(self.camera_frame.set_width, 15, + self.camera_frame.move_to, 0) finalFormula=TextMobject("Hence","$T_{ n }(x)$","=","$f(1)+f'(1)(x-1)+\\frac { f''(1) }{ 2! }(x-1)^2+..+\\frac { { f }^{ n }(1) }{ n! } { (x-1) }^{ n }$") finalFormula.scale(0.8) @@ -192,4 +236,4 @@ class graphScene(GraphScene): self.play(FadeOut(self.axes),FadeOut(textFinal),FadeOut(thirdGraph),FadeOut(trTextGrup),FadeOut(mainfunction),FadeOut(fx),FadeOut(coeff[0]),FadeOut(coeff[1]),FadeOut(coeff[2])) self.play(Write(finalFormula)) - self.wait(2) + self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/video3_radiusOfConvergence.py b/FSF-2020/calculus/series-and-transformations/Taylor Series/video3_radiusOfConvergence.py index a68afb6..52f07bb 100644 --- a/FSF-2020/calculus/series-and-transformations/Taylor Series/video3_radiusOfConvergence.py +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/video3_radiusOfConvergence.py @@ -2,7 +2,7 @@ from manimlib.imports import* import math -class graphScene(GraphScene): +class graphScene(GraphScene,MovingCameraScene): CONFIG = { "x_min": -8, "x_max": 8, @@ -16,12 +16,15 @@ class graphScene(GraphScene): "exclude_zero_label": True, "x_labeled_nums": range(-8, 8, 1), } + def setup(self): + GraphScene.setup(self) + MovingCameraScene.setup(self) def construct(self): x_each_unit = self.x_axis_width / (self.x_max - self.x_min) y_each_unit = self.y_axis_height / (self.y_max - self.y_min) - self.setup_axes(animate=True) + self.setup_axes(animate=True,scalee=1) lnx=self.get_graph(lambda x:math.log2(x),color=RED,x_min=0.01,x_max=8) @@ -98,14 +101,23 @@ class graphScene(GraphScene): circle=Circle(radius=ORIGIN+x_each_unit*2,color=PURPLE_E) circle.shift(ORIGIN+RIGHT*x_each_unit*2) - radiusLine=Line(start=ORIGIN+x_each_unit*RIGHT*2,end=ORIGIN+x_each_unit*4*RIGHT,color=PURPLE_E) + radiusLine=Line(start=ORIGIN+x_each_unit*RIGHT*2,end=ORIGIN+x_each_unit*2*RIGHT+y_each_unit*3*UP,color=PURPLE_E) radius=TextMobject("$R$") radius.set_color(RED) radius.scale(0.5) - radius.shift(ORIGIN+RIGHT*x_each_unit*2.45+DOWN*y_each_unit*0.6) + radius.shift(ORIGIN+RIGHT*x_each_unit*2.45+UP*y_each_unit*2.2) + rText=TextMobject("R",":","Radius of Convergence").scale(0.3).shift(x_each_unit*RIGHT*2+UP*y_each_unit*3.3).set_color_by_tex_to_color_map({"R":RED,"Radius of Convergence":YELLOW}) self.play(FadeOut(equations[6]),Write(circle)) self.wait(0.6) self.play(Write(radiusLine)) self.play(FadeIn(radius)) - self.wait(2) + self.wait(0.7) + self.camera_frame.save_state() + self.play(self.camera_frame.set_width, 8, + self.camera_frame.move_to, y_each_unit*UP+x_each_unit*2*RIGHT) + self.play(Write(rText)) + self.wait(1) + self.play(self.camera_frame.set_width, 15, + self.camera_frame.move_to,0) + self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/calculus/series-and-transformations/Taylor Series/video4_DivergentRemainder.py b/FSF-2020/calculus/series-and-transformations/Taylor Series/video4_DivergentRemainder.py index 5389039..1f41c97 100644 --- a/FSF-2020/calculus/series-and-transformations/Taylor Series/video4_DivergentRemainder.py +++ b/FSF-2020/calculus/series-and-transformations/Taylor Series/video4_DivergentRemainder.py @@ -79,4 +79,4 @@ class graphScene(GraphScene): self.play(Write(increasingText)) self.play(FadeIn(followupText)) self.wait(2) - +
\ No newline at end of file diff --git a/FSF-2020/calculus/series-and-transformations/Z-Transform/README.md b/FSF-2020/calculus/series-and-transformations/Z-Transform/README.md new file mode 100644 index 0000000..c626bdf --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Z-Transform/README.md @@ -0,0 +1,9 @@ +#### Sampling + + +#### Z Transform of a delta function + + +#### Region of convergence + + diff --git a/FSF-2020/calculus/series-and-transformations/Z-Transform/gifs/file1.gif b/FSF-2020/calculus/series-and-transformations/Z-Transform/gifs/file1.gif Binary files differnew file mode 100644 index 0000000..d21aa59 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Z-Transform/gifs/file1.gif diff --git a/FSF-2020/calculus/series-and-transformations/Z-Transform/gifs/file2.gif b/FSF-2020/calculus/series-and-transformations/Z-Transform/gifs/file2.gif Binary files differnew file mode 100644 index 0000000..203be8d --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Z-Transform/gifs/file2.gif diff --git a/FSF-2020/calculus/series-and-transformations/Z-Transform/gifs/file3.gif b/FSF-2020/calculus/series-and-transformations/Z-Transform/gifs/file3.gif Binary files differnew file mode 100644 index 0000000..0f100f1 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Z-Transform/gifs/file3.gif diff --git a/FSF-2020/calculus/series-and-transformations/Z-Transform/video1_Sampling.py b/FSF-2020/calculus/series-and-transformations/Z-Transform/video1_Sampling.py new file mode 100644 index 0000000..47615e3 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Z-Transform/video1_Sampling.py @@ -0,0 +1,81 @@ +from manimlib.imports import * +import math + +def func(x): + return math.pow(x,3)-2*math.pow(x,2)-x+3 + +class graphScene(GraphScene): + CONFIG = { + "x_min": -3, + "x_max": 3, + "y_min": -4, + "y_max": 4, + "x_tick_frequency": 0.2, + "graph_origin": ORIGIN, + "function_color": RED, + "axes_color": BLUE, + "x_axis_label": "$t$", + "y_axis_label": "$f(t)$", + "exclude_zero_label": True, + "x_labeled_nums": range(-3, 4, 1), + "y_axis_height": 5, + "x_axis_width": 9, + } + + def construct(self): + x_each_unit = self.x_axis_width / (self.x_max - self.x_min) + y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + + fx=TextMobject("$f(t) = { t }^{ 3 }{ -2t }^{ 2 }-t+3$").set_color(RED).to_corner(UP+RIGHT).scale(0.4) + self.setup_axes(animate=True,scalee=1) + function=self.get_graph(lambda x:math.pow(x,3)-2*math.pow(x,2)-x+3,color=RED,x_min=-1,x_max=2) + functionArea=self.get_riemann_rectangles(function,x_min=-1,x_max=2,dx=0.01,start_color=GREEN,end_color=YELLOW,stroke_color=GREEN,fill_opacity=0.8) + functionDot=Dot(point=self.graph_origin,radius=0.065,color=WHITE) + aboveText1=TextMobject("Continuous","Time Function").shift(4*RIGHT+2*UP).scale(0.4).set_color_by_tex_to_color_map({"Continuous":YELLOW,"Time Function":BLUE}) + aboveText2=TextMobject("Discrete","Time Function").shift(4*RIGHT+2*UP).scale(0.4).set_color_by_tex_to_color_map({"Time Function":BLUE,"Discrete":YELLOW}) + + bottomText1=TextMobject("Instead of considering the","function","over the","entire $t$,").shift(4.5*RIGHT+3*DOWN).scale(0.4).set_color_by_tex_to_color_map({"entire $t$,":RED,"function":YELLOW}) + bottomText2=TextMobject("We consider only at","certain $t$").shift(4.5*RIGHT+3*DOWN).scale(0.4).set_color_by_tex_to_color_map({"certain $t$":RED}) + + self.play(ShowCreation(function),Write(fx),FadeIn(aboveText1)) + self.wait(0.7) + self.play(Write(bottomText1)) + self.play(ShowCreation(functionArea),MoveAlongPath(functionDot,function)) + self.wait(0.7) + self.play(FadeOut(bottomText1)) + self.play(Write(bottomText2),FadeOut(aboveText1)) + + dots=[Dot(radius=0.05) for i in range(10)] + dotShifts=[-1,-0.7,-0.4,0,0.3,0.6,1,1.3,1.6,2] + lines=[] + for x in dotShifts: + lines.append(Line(start=(x*x_each_unit,func(x)*y_each_unit,0),end=(x*x_each_unit,0,0),color=GREEN)) + for i in range(10): + dots[i].shift(ORIGIN+RIGHT*x_each_unit*dotShifts[i]+y_each_unit*UP*func(dotShifts[i])) + updatedGraph=VGroup(dots[0], + dots[1], + dots[2], + dots[3], + dots[4], + dots[5], + dots[6], + dots[7], + dots[8], + dots[9]) + updatedGraph1=VGroup( + lines[0], + lines[1], + lines[2], + lines[3], + lines[4], + lines[5], + lines[6], + lines[7], + lines[8], + lines[9]) + + self.play(FadeOut(functionDot)) + self.play(FadeOut(function),FadeIn(updatedGraph)) + self.play(FadeOut(functionArea),FadeIn(updatedGraph1)) + self.play(FadeOut(bottomText2),FadeIn(aboveText2)) + self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/calculus/series-and-transformations/Z-Transform/video2_ZTransformOfDelta.py b/FSF-2020/calculus/series-and-transformations/Z-Transform/video2_ZTransformOfDelta.py new file mode 100644 index 0000000..3063aa6 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Z-Transform/video2_ZTransformOfDelta.py @@ -0,0 +1,121 @@ +from manimlib.imports import * +import numpy as np +import math + +class deltaTransformation(GraphScene): + CONFIG = { + "x_min": -3, + "x_max": 3, + "y_min": -5, + "y_max": 5, + "graph_origin": ORIGIN, + "function_color": RED, + "axes_color": BLUE, + "x_axis_label": "$t$", + "y_axis_label": "$f(t)$", + "x_labeled_nums": range(-3, 4, 1), + # "y_axis_height": 4, + # "x_axis_width": 6, + } + def construct(self): + x_each_unit = self.x_axis_width / (self.x_max - self.x_min) + y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + self.setup_axes(animate=True,scalee=0.8) + function=TextMobject("$f(t) = 2{ \delta }_{ 0 }(t)+3{ \delta }_{ 1 }(t)+4{ \delta }_{ 2 }(t)$").scale(0.4).shift(5*RIGHT+3*UP).set_color(RED) + self.play(FadeIn(function)) + twoDGraph=[ + Line(start=(0,0,0),end=(0,2*y_each_unit,0),color=GREEN), + Line(start=(1*x_each_unit,0,0),end=(x_each_unit,3*y_each_unit,0),color=GREEN), + Line(start=(2*x_each_unit,0,0),end=(2*x_each_unit,4*y_each_unit,0),color=GREEN) + ] + groupGraph=VGroup(twoDGraph[1],twoDGraph[2],self.axes,twoDGraph[0]) + self.play(Write(twoDGraph[0]),ShowCreation(twoDGraph[1]),ShowCreation(twoDGraph[2])) + self.wait(1.2) + self.play(ApplyMethod(groupGraph.scale,0.7)) + self.play(ApplyMethod(groupGraph.shift,5*LEFT),ApplyMethod(function.move_to,5*LEFT+3*UP)) + self.graph_origin=2*RIGHT+2.5*DOWN + self.x_axis_width=6 + self.x_axis_label="$|z|$" + self.y_axis_label="$|F(t)|$" + self.x_min=-3 + self.x_max=6 + self.y_min=-1 + self.y_max=7 + self.x_labeled_nums=range(-3,7,1) + self.setup_axes(animate=True,scalee=0.6) + x_each_unit = self.x_axis_width / (self.x_max - self.x_min) + y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + rightSideGraphs=[ + self.get_graph(lambda x:2,x_min=0,x_max=6,color=GREEN), + self.get_graph(lambda x:2+3/x,x_min=0.6,x_max=6,color=GREEN), + self.get_graph(lambda x:2+(3/x)+(4/x**2),x_min=1.24,x_max=6,color=GREEN) + ] + graphCoeff=[ + TextMobject("$2$").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*2+UP*y_each_unit*2+DOWN*y_each_unit*0.5).set_color(RED), + TextMobject("$2+\\frac { 3 }{ |z| }$").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*3+UP*y_each_unit*2).set_color(RED), + TextMobject("$2+\\frac { 3 }{ |z| } +\\frac { 4 }{ { |z| }^{ 2 } } $").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*3.5+UP*y_each_unit*2).set_color(RED) + ] + self.play(ReplacementTransform(twoDGraph[0],rightSideGraphs[0]),FadeIn(graphCoeff[0])) + self.wait(0.5) + self.play(FadeOut(rightSideGraphs[0]),ReplacementTransform(twoDGraph[1],rightSideGraphs[1]),ReplacementTransform(graphCoeff[0],graphCoeff[1])) + self.wait(0.5) + self.play(FadeOut(rightSideGraphs[1]),ReplacementTransform(twoDGraph[2],rightSideGraphs[2]),ReplacementTransform(graphCoeff[1],graphCoeff[2])) + + self.wait(2) + + +class graphCont(GraphScene,MovingCameraScene): + CONFIG = { + "x_min": -3, + "x_max": 6, + "y_min": -1, + "y_max": 7, + "graph_origin": 2*RIGHT+2.5*DOWN, + "function_color": RED, + "axes_color": BLUE, + "x_axis_label": "$|z|$", + "y_axis_label": "$|F(t)|$", + "exclude_zero_label": True, + "x_labeled_nums": range(-3, 7, 1), + "x_axis_width": 6, + } + def setup(self): + GraphScene.setup(self) + MovingCameraScene.setup(self) + + def construct(self): + x_each_unit = self.x_axis_width / (self.x_max - self.x_min) + y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + + coeff=TextMobject("$2+\\frac { 3 }{ |z| } +\\frac { 4 }{ { |z| }^{ 2 } } $").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*3.5+UP*y_each_unit*2).set_color(RED) + self.setup_axes(scalee=0.6) + graph=self.get_graph(lambda x:2+(3/x)+(4/x**2),x_min=1.24,x_max=6,color=GREEN) + xAxis=self.get_graph(lambda x:0,x_min=1.24,x_max=6).shift(3*LEFT) + self.add(graph) + self.add(coeff) + self.play(ApplyMethod((self.axes).shift,3*LEFT),ApplyMethod(coeff.shift,3*LEFT),ApplyMethod(graph.shift,3*LEFT)) + topText=TextMobject("Here we get","output","for","any value of $|z|$").scale(0.4).shift(3*UP+3*RIGHT).set_color_by_tex_to_color_map({"output":YELLOW,"any value of $|z|$":BLUE}) + topText1=TextMobject("Except for $|z|=0$").scale(0.7).shift(2.5*UP+3*RIGHT).set_color(RED) + dot1=Dot(color=WHITE,radius=0.06) + dot2=Dot(color=WHITE,radius=0.06) + self.play(Write(topText)) + self.play(MoveAlongPath(dot1,graph),MoveAlongPath(dot2,xAxis),run_time=2) + self.play(Write(topText1)) + self.play(FadeOut(dot1),FadeOut(dot2)) + self.wait(0.5) + path=self.get_graph(lambda x:2+(3/x)+(4/x**2),x_min=1.24,x_max=0.8) + path1=self.get_graph(lambda x:0,x_min=1.24,x_max=0.8) + graphUpdated=self.get_graph(lambda x:2+(3/x)+(4/x**2),x_min=0.8,x_max=6,color=GREEN) + self.camera_frame.save_state() + self.play(FadeOut(graph),Write(graphUpdated)) + self.play(self.camera_frame.set_width, 30, + MoveAlongPath(dot1,path),MoveAlongPath(dot2,path1),run_time=2) + self.wait(1) + + self.play(FadeOut(dot1),FadeOut(dot2),FadeOut(graphUpdated),FadeIn(graph),self.camera_frame.set_width,15) + self.wait(1) + + + + + diff --git a/FSF-2020/calculus/series-and-transformations/Z-Transform/video3_RegionOfConvergence.py b/FSF-2020/calculus/series-and-transformations/Z-Transform/video3_RegionOfConvergence.py new file mode 100644 index 0000000..bdfd8b3 --- /dev/null +++ b/FSF-2020/calculus/series-and-transformations/Z-Transform/video3_RegionOfConvergence.py @@ -0,0 +1,144 @@ +from manimlib.imports import * +import numpy as np +import math + +class graph1(GraphScene): + CONFIG = { + "x_min": -3, + "x_max": 5, + "y_min": -1, + "y_max": 1, + "graph_origin": ORIGIN, + "function_color": RED, + "axes_color": BLUE, + "x_axis_label": "$n$", + "y_axis_label": "$x(n)$", + "x_labeled_nums": range(-3, 6, 1), + "y_axis_height": 7, + "y_tick_frequency": 0.1, + } + def func(self,x,n): + summ=0 + for i in range(n+1): + summ+=(1/(math.pow(x,i))) + return summ + + def finalFunc(self,x): + if(x!=0): + return 1/(1-(1/(2*x))) + + + def construct(self): + x_each_unit = self.x_axis_width / (self.x_max - self.x_min) + y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + self.setup_axes(animate=True,scalee=0.8) + function=TextMobject("$X(t)=\sum _{ n=0 }^{ \infty }{ { (0.5) }^{ n }{ z }^{ -n } }$").scale(0.4).shift(5*RIGHT+3*UP).set_color(RED) + self.play(FadeIn(function)) + twoDGraph=[] + for i in range(5): + twoDGraph.append(Line(start=(i*x_each_unit,0,0),end=(i*x_each_unit,math.pow(0.5,i)*y_each_unit,0),color=GREEN)) + + groupGraph=VGroup(self.axes,twoDGraph[0],twoDGraph[1],twoDGraph[2],twoDGraph[3],twoDGraph[4]) + self.play(Write(twoDGraph[0]),ShowCreation(twoDGraph[1]),ShowCreation(twoDGraph[2]),ShowCreation(twoDGraph[3]),ShowCreation(twoDGraph[4])) + self.wait(1.2) + + self.play(ApplyMethod(groupGraph.scale,0.7)) + self.play(ApplyMethod(groupGraph.shift,6*LEFT),ApplyMethod(function.move_to,5*LEFT+3*UP)) + + someText1=TextMobject("Since it is a","summation","of","infinite terms",", it might").shift(2*RIGHT+2*UP).scale(0.5).set_color_by_tex_to_color_map({"summation":YELLOW,"infinite terms":BLUE}) + someText2=TextMobject("Converge","or","Diverge").shift(2*RIGHT+0.5*DOWN+2*UP).scale(0.7).set_color_by_tex_to_color_map({"Converge":GREEN,"Diverge":RED}) + someText3=TextMobject("depending upon","$|z|$").shift(2*RIGHT+UP).scale(0.5).set_color_by_tex_to_color_map({"$|z|$":YELLOW}) + self.play(Write(someText1)) + self.play(FadeIn(someText2)) + self.play(Write(someText3)) + self.wait(1) + self.play(FadeOut(someText1),FadeOut(someText2),FadeOut(someText3)) + + self.graph_origin=2*RIGHT+DOWN + self.x_axis_width=6 + self.y_axis_height=5 + self.y_tick_frequency=1 + self.x_axis_label="$|z|$" + self.y_axis_label="$|X(n)|$" + self.x_min=-3 + self.x_max=5 + self.y_min=-1 + self.y_max=5 + self.x_labeled_nums=range(-3,6,1) + self.setup_axes(animate=True,scalee=0.6) + x_each_unit = self.x_axis_width / (self.x_max - self.x_min) + y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + rightSideGraphs=[] + xmins=[0,0.25,0.65,0.9,1] + for i in range(5): + rightSideGraphs.append(self.get_graph(lambda x:self.func(x,i),x_min=xmins[i],x_max=5,color=GREEN)) + rightSideGraphs.append(self.get_graph(lambda x:1/(1-(1/(2*x))),x_min=0.63,x_max=5,color=GREEN)) + + graphCoeff=[ + TextMobject("$1$").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*2+0.65*UP*y_each_unit*2+DOWN*y_each_unit*0.5).set_color(RED), + TextMobject("$1+\\frac { 1 }{ 2|z| }$").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*2+UP*y_each_unit).set_color(RED), + TextMobject("$1+\\frac { 1 }{ 2|z| } +\\frac { 1 }{ { 2|z| }^{ 2 } } $").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*2+UP*y_each_unit).set_color(RED), + TextMobject("$1+\\frac { 1 }{ 2|z| } +\\frac { 1 }{ { (2|z|) }^{ 2 } } +\\frac { 1 }{ { (2|z|) }^{ 3 } }$").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*2+UP*y_each_unit).set_color(RED), + TextMobject("$1+\\frac { 1 }{ 2|z| } +\\frac { 1 }{ { (2|z|) }^{ 2 } } +\\frac { 1 }{ { (2|z|) }^{ 3 } } +\\frac { 1 }{ (2|z|)^{ 4 } } $").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*2+UP*y_each_unit).set_color(RED), + TextMobject("$\\frac { 1 }{ (1-\\frac { 1 }{ 2z } ) } $").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*2+UP*y_each_unit).set_color(RED) + ] + + self.play(ReplacementTransform(twoDGraph[0],rightSideGraphs[0]),FadeIn(graphCoeff[0])) + self.wait(0.5) + self.play(FadeOut(rightSideGraphs[0]),ReplacementTransform(twoDGraph[1],rightSideGraphs[1]),ReplacementTransform(graphCoeff[0],graphCoeff[1])) + self.wait(0.5) + self.play(FadeOut(rightSideGraphs[1]),ReplacementTransform(twoDGraph[2],rightSideGraphs[2]),ReplacementTransform(graphCoeff[1],graphCoeff[2])) + self.wait(0.5) + self.play(FadeOut(rightSideGraphs[2]),ReplacementTransform(twoDGraph[3],rightSideGraphs[3]),ReplacementTransform(graphCoeff[2],graphCoeff[3])) + self.wait(0.5) + self.play(FadeOut(rightSideGraphs[3]),ReplacementTransform(twoDGraph[4],rightSideGraphs[4]),ReplacementTransform(graphCoeff[3],graphCoeff[4])) + self.wait(0.5) + self.play(FadeOut(rightSideGraphs[4]),ShowCreation(rightSideGraphs[5]),ReplacementTransform(graphCoeff[4],graphCoeff[5])) + + self.wait(2) + # #self.play(FadeOut(self.axes),FadeOut(function),FadeOut(twoDGraph[0]),FadeOut(twoDGraph[1]),FadeOut(twoDGraph[2])) + + +class graphCont(GraphScene,MovingCameraScene): + CONFIG = { + "x_min": -3, + "x_max": 5, + "y_min": -1, + "y_max": 5, + "graph_origin": 2*RIGHT+DOWN, + "function_color": RED, + "axes_color": BLUE, + "x_axis_label": "$|z|$", + "y_axis_label": "$|X(n)|$", + "x_labeled_nums": range(-3, 6, 1), + "x_axis_width": 6, + "y_axis_height": 5 + } + def setup(self): + GraphScene.setup(self) + MovingCameraScene.setup(self) + + def construct(self): + x_each_unit = self.x_axis_width / (self.x_max - self.x_min) + y_each_unit = self.y_axis_height / (self.y_max - self.y_min) + + coeff=TextMobject("$\\frac { 1 }{ (1-\\frac { 1 }{ 2z } ) } $").scale(0.4).shift(self.graph_origin+x_each_unit*RIGHT*2+UP*y_each_unit).set_color(RED) + self.setup_axes(scalee=0.6) + graph=self.get_graph(lambda x:1/(1-(1/(2*x))),x_min=0.63,x_max=5,color=GREEN) + + self.add(graph) + self.add(coeff) + + self.play(ApplyMethod((self.axes).shift,3*LEFT),ApplyMethod(coeff.shift,3*LEFT),ApplyMethod(graph.shift,3*LEFT)) + self.wait(1) + + dashLine=DashedLine(start=self.graph_origin+3*LEFT+0.5*x_each_unit*RIGHT,end=self.graph_origin+3*LEFT+0.5*x_each_unit*RIGHT+y_each_unit*UP*5,color=YELLOW) + pt=TextMobject("0.5").scale(0.3).shift(self.graph_origin+3*LEFT+0.5*x_each_unit*RIGHT+DOWN*y_each_unit*0.3) + self.play(Write(dashLine)) + self.play(Write(pt)) + self.wait(0.6) + rectRegion=Rectangle(height=y_each_unit*5,width=x_each_unit*5,fill_color=WHITE,fill_opacity=0.3,opacity=0.3,color=BLACK).shift(1.6*RIGHT*x_each_unit+0.5*DOWN*y_each_unit+1.5*UP) + self.play(ShowCreation(rectRegion)) + text=TextMobject("Region Of Convergence!").scale(0.4).shift(4.6*RIGHT+1.5*UP).set_color(GREEN) + self.play(FadeIn(text)) + self.wait(2) diff --git a/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/README.md b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/README.md new file mode 100644 index 0000000..0305ba7 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/README.md @@ -0,0 +1,18 @@ +# Contributer: Archit Sangal +My Github Account : <a href="https://github.com/architsangal">architsangal</a> +<br/></br> + +## Sub-Topics Covered: ++ Gramm-Schmidt Orthogonalization Process + +#### Video 1: Introduction to Gram-Schmidt Orthogonalization Process + + +#### Video 2: Obtaining orthogonal vectors using projections + + +#### Video 3: Visual Explanation of how Gram-Schmidt Orthogonalization Process give mutually orthonormal vectors + + +#### Video 4: Example of Orthonormal Vectors which are different from standard basis +
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file1_introduction.py b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file1_introduction.py new file mode 100644 index 0000000..ccd23c9 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file1_introduction.py @@ -0,0 +1,33 @@ +from manimlib.imports import * + +class Orthonormal(Scene): + def construct(self): + Centre = DOWN + arrow_1 = Arrow(start = Centre+ORIGIN,end = Centre+1.414*(UP+RIGHT)) + arrow_2 = Arrow(start = Centre+ORIGIN,end = Centre+2*UP) + arrow_1.scale(1.35) + arrow_2.scale(1.35) + text = TextMobject("This is a set of linearly independent vectors") + text.scale(0.75) + text.move_to(3*UP+3*LEFT) + text.set_color(PURPLE_E) + arrow_1.set_color(PURPLE_E) + arrow_2.set_color(PURPLE_E) + self.play(Write(text)) + self.play(ShowCreation(arrow_1), ShowCreation(arrow_2)) + self.wait(2) + text1 = TextMobject("After we apply Gram-Schmidt Orthogonalization Process to set of linearly independent vectors") + text1.scale(0.6) + text1.move_to(3*UP+2*LEFT) + text1.set_color(GREEN) + arrow_a = Arrow(start = Centre+ORIGIN,end = Centre+0.707*(UP+RIGHT)) + arrow_a.set_color(GREEN) + arrow_a.scale(2) + self.play(Transform(text,text1)) + self.wait(2) + self.play(Transform(arrow_1,arrow_a)) + arrow_b = Arrow(start = Centre+ORIGIN,end = Centre+0.707*(UP+LEFT)) + arrow_b.set_color(GREEN) + arrow_b.scale(2) + self.play(Transform(arrow_2,arrow_b)) + self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file2_projections.py b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file2_projections.py new file mode 100755 index 0000000..dd4b8d4 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file2_projections.py @@ -0,0 +1,79 @@ +from manimlib.imports import * + +class Projections(GraphScene): + CONFIG = { + "x_min": -6, + "x_max": 6, + "y_min": -4, + "y_max": 4, + "graph_origin" : ORIGIN , + } + def construct(self): + + self.setup_axes(animate=True) + + XTD = self.x_axis_width/(self.x_max-self.x_min) + YTD = self.y_axis_height/(self.y_max-self.y_min) + + arrow_a = Arrow(start = ORIGIN, end = 4*XTD*RIGHT) + arrow_a.scale(1.2) + arrow_a.set_color(DARK_BLUE) + arrow_b = Arrow(start = ORIGIN, end = 2*YTD*UP+2*XTD*RIGHT) + arrow_b.scale(1.3) + arrow_b.set_color(DARK_BLUE) + self.play(ShowCreation(arrow_a), ShowCreation(arrow_b)) + + text = TextMobject(r"Consider 2 linearly independent vectors $a$ and $b$") + text.set_color(DARK_BLUE) + text.scale(0.6) + text.move_to(3*YTD*UP+5*XTD*LEFT) + text_a = TextMobject("a") + text_a.move_to(0.4*YTD*DOWN+3*XTD*RIGHT) + text_a.set_color(DARK_BLUE) + text_b = TextMobject("b") + text_b.move_to(1.5*YTD*UP+RIGHT*XTD) + text_b.set_color(DARK_BLUE) + + self.play(Write(text),Write(text_a), Write(text_b)) + self.wait() + + arrow_b_copy = Arrow(start = ORIGIN, end = 2*YTD*UP+2*XTD*RIGHT) + arrow_b_copy.scale(1.25) + + arrow_p = Arrow(start = ORIGIN, end = 2*XTD*RIGHT) + arrow_p.scale(1.5) + arrow_p.set_color(GOLD_E) + + text_p = TextMobject("p") + text_p.move_to(0.25*DOWN+RIGHT) + text_p.set_color(GOLD_E) + + self.play(FadeOut(text), Transform(arrow_b_copy,arrow_p), FadeOut(text_a), FadeOut(text_b)) + text = TextMobject(r"$p$ is the projection of $b$ on $a$") + text.set_color(GOLD_E) + text.move_to(3*UP+4*LEFT) + text.scale(0.8) + self.play(Write(text),Write(text_p)) + self.wait() + + self.play(FadeIn(text_a), FadeIn(text_b)) + + arrow_o = Arrow(start = 2*XTD*RIGHT, end = 2*YTD*UP+2*XTD*RIGHT) + arrow_o.scale(1.5) + arrow_o.set_color(GREEN_E) + + text_o = TextMobject("b-p") + text_o.move_to(UP*YTD+2.7*XTD*RIGHT) + text_o.set_color(GREEN_E) + + self.play(ShowCreation(arrow_o)) + self.play(FadeOut(text),Write(text_o)) + + text = TextMobject(r"Observe, ($b-p$) is orthogonal to $a$") + text.set_color(GREEN_E) + text.move_to(2*DOWN+4*LEFT) + text.scale(0.8) + self.play(Write(text)) + self.wait(2) + + self.play(FadeOut(self.axes), FadeOut(arrow_a), FadeOut(arrow_b), FadeOut(arrow_b_copy), FadeOut(arrow_o), FadeOut(text_a), FadeOut(text_b), FadeOut(text_o), FadeOut(text_p), FadeOut(text))
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file3_orthonormal.py b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file3_orthonormal.py new file mode 100644 index 0000000..af51fc6 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file3_orthonormal.py @@ -0,0 +1,333 @@ +from manimlib.imports import * + +class Algo(ThreeDScene): + def construct(self): + + axes = ThreeDAxes(x_min = -5,x_max=5,y_min=-3,y_max=3,z_min=-4,z_max=4) + self.play(ShowCreation(axes)) + + text = TextMobject(r"This is the vector $\beta_1(=\left[\begin{array}{c} 4\\0\\0 \end{array}\right])$") + text.set_color(GREEN) + text.scale(0.6) + text.move_to(3*UP+5*LEFT) + self.play(Write(text)) + + arrow_a = Arrow(start = ORIGIN, end = 4*RIGHT) + arrow_a.set_color(GREEN) + arrow_a.scale(1.15) + self.play(ShowCreation(arrow_a)) + + text_a = TextMobject(r"$\beta_1$") + text_a.move_to(0.4*DOWN+3*RIGHT) + text_a.set_color(GREEN) + text_a.scale(0.75) + self.play(Write(text_a)) + self.wait() + self.play(FadeOut(text)) + + text = TextMobject(r"Normalize $\beta_1$ to get $\alpha_1$") + text.set_color(DARK_BLUE) + text.scale(0.75) + text.move_to(3*UP+5*LEFT) + self.play(Write(text)) + + alpha_1 = Arrow(start = ORIGIN,end = RIGHT) + alpha_1.scale(1.9) + alpha_1.set_color(DARK_BLUE) + text_alpha_1 = TextMobject(r"$\alpha_1$") + text_alpha_1.move_to(0.4*DOWN+RIGHT) + text_alpha_1.set_color(DARK_BLUE) + text_alpha_1.scale(0.75) + self.play(Transform(text_a,text_alpha_1), Transform(arrow_a,alpha_1)) + self.wait() + self.play(FadeOut(text)) + + text = TextMobject(r"Consider another vector $\beta_2(=\left[\begin{array}{c} 2\\2\\0 \end{array}\right])$") + text1 = TextMobject(r"which is linearly independent to $\beta_1$") + text.set_color(GREEN) + text1.set_color(GREEN) + text.scale(0.6) + text1.scale(0.6) + text.move_to(3*UP+4*LEFT) + text1.move_to(2*UP+4*LEFT) + self.play(Write(text)) + self.play(Write(text1)) + + arrow_b = Arrow(start = ORIGIN, end = 2*UP+2*RIGHT) + arrow_b.scale(1.2) + arrow_b.set_color(GREEN) + text_b = TextMobject(r"$\beta_2$") + text_b.move_to(1.5*UP+RIGHT) + text_b.set_color(GREEN) + text_b.scale(0.75) + + self.play(ShowCreation(arrow_b), Write(text_b)) + self.wait() + + arrow_b_copy = Arrow(start = ORIGIN, end = 2*UP+2*RIGHT) + arrow_b_copy.scale(1.2) + + arrow_p = Arrow(start = ORIGIN, end = 2*RIGHT) + arrow_p.scale(1.35) + arrow_p.set_color(GOLD_E) + + text_p = TextMobject("p") + text_p.move_to(0.25*DOWN+RIGHT) + text_p.set_color(GOLD_E) + + self.play(FadeOut(text), FadeOut(text1), Transform(arrow_b_copy,arrow_p), FadeOut(text_a), FadeOut(text_b)) + text = TextMobject(r"$p$ is the projection of $\beta_2$ on $\alpha_1$") + text.set_color(GOLD_E) + text.move_to(3*UP+4*LEFT) + text.scale(0.8) + self.play(Write(text),Write(text_p)) + self.wait() + + self.play(FadeIn(text_b)) + + arrow_o = Arrow(start = 2*RIGHT, end = 2*UP+2*RIGHT) + arrow_o.scale(1.35) + arrow_o.set_color(PURPLE_E) + + text_o = TextMobject(r"$\beta_2-p$") + text_o.move_to(UP+2.7*RIGHT) + text_o.scale(0.75) + text_o.set_color(PURPLE_E) + + self.play(ShowCreation(arrow_o)) + self.play(FadeOut(text),Write(text_o)) + + text = TextMobject(r"$\beta_2-p$ is orthogonal to p") + text1 = TextMobject(r"(and hence orthogonal to $\alpha_1$ also)") + text.set_color(PURPLE_E) + text1.set_color(PURPLE_E) + text.scale(0.7) + text1.scale(0.7) + text.move_to(3*UP+4*LEFT) + text1.move_to(2.5*UP+4*LEFT) + self.play(Write(text)) + self.play(Write(text1)) + self.wait(2) + + self.play(FadeOut(text_p), FadeIn(arrow_a), FadeOut(text), FadeOut(text1), FadeOut(arrow_b_copy), FadeOut(arrow_p), FadeOut(text_b), FadeOut(arrow_b)) + self.play(ApplyMethod(arrow_o.move_to,UP), ApplyMethod(text_o.move_to,RIGHT+UP)) + + text = TextMobject(r"Now, Normalize $\beta_2-p$") + text.set_color(DARK_BLUE) + text.scale(0.6) + text.move_to(3*UP+4*LEFT) + self.play(Write(text)) + + alpha_2 = Arrow(start = ORIGIN,end = UP) + alpha_2.scale(1.9) + alpha_2.set_color(DARK_BLUE) + text_alpha_2 = TextMobject(r"$\alpha_2$") + text_alpha_2.move_to(0.4*LEFT+UP) + text_alpha_2.set_color(DARK_BLUE) + text_alpha_2.scale(0.75) + self.play(Transform(text_o,text_alpha_2), Transform(arrow_o,alpha_2), FadeIn(text_a)) + self.wait() + self.play(FadeOut(text),FadeOut(text_a),FadeOut(text_o)) + + self.add(axes) + ############################################################################# + axis = TextMobject(r"$\alpha_1$",r"$\alpha_2$",r"$\alpha_3$",r"$\beta_3$",r"$\alpha_3$",r"$\alpha_3$",r"$\alpha_3$",r"$\alpha_3$") + axis.scale(0.5) + axis[0].move_to(0.5*RIGHT+[0,0,-0.5]) + axis[1].move_to(0.5*UP+[0,0,-0.5]) + axis[2].move_to(np.array([0,0,0.5])) + axis[3].move_to(np.array([1,1,1.5])) + self.add_fixed_orientation_mobjects(axis[0]) + self.add_fixed_orientation_mobjects(axis[1]) + ############################################################################# + + text = TextMobject(r"These are the same two orthonormal vectors $\alpha_{1}$ and $\alpha_{2}$") + text.scale(0.6) + text.set_color(DARK_BLUE) + self.add_fixed_in_frame_mobjects(text) + text.move_to(3*(DOWN+RIGHT)) + self.play(Write(text)) + + self.move_camera(phi=60*DEGREES,theta=45*DEGREES,run_time=3) + self.begin_ambient_camera_rotation(rate=0.3) + + line1 = Line(start = ORIGIN,end = 1*RIGHT) + line1.set_color(DARK_BLUE) + tip1 = Polygon(RIGHT,0.8*RIGHT-0.2*DOWN,0.8*RIGHT-0.2*UP) + tip1.set_opacity(1) + tip1.set_fill(DARK_BLUE) + tip1.set_color(DARK_BLUE) + + arrow2 = Line(start = ORIGIN,end = 1*UP) + arrow2.set_color(DARK_BLUE) + tip2 = Polygon(UP,0.8*UP-0.2*RIGHT,0.8*UP-0.2*LEFT) + tip2.set_opacity(1) + tip2.set_fill(DARK_BLUE) + tip2.set_color(DARK_BLUE) + arrow2.set_color(DARK_BLUE) + + self.play(ShowCreation(line1), ShowCreation(tip1), ShowCreation(arrow2), ShowCreation(tip2), FadeOut(arrow_a), FadeOut(arrow_o)) + self.wait() + + a_line = Line(start = ORIGIN,end = 2*UP+2*RIGHT+[0,0,2]) + a_line.set_color(GOLD_E) + a_tip = Polygon(2*UP+2*RIGHT+[0,0,2],2*UP+1.6*RIGHT+[0,0,1.8],1.6*UP+2*RIGHT+[0,0,1.8]) + a_tip.set_opacity(1) + a_tip.set_fill(GOLD_E) + a_tip.set_color(GOLD_E) + + a_line_c1 = Line(start = ORIGIN,end = 2*UP+2*RIGHT+[0,0,2]) + a_line_c1.set_color(GOLD_E) + a_tip_c1 = Polygon(2*UP+2*RIGHT+[0,0,2],2*UP+1.6*RIGHT+[0,0,1.8],1.6*UP+2*RIGHT+[0,0,1.8]) + a_tip_c1.set_opacity(1) + a_tip_c1.set_fill(GOLD_E) + a_tip_c1.set_color(GOLD_E) + + self.play(FadeOut(text), ShowCreation(a_line), ShowCreation(a_tip), ShowCreation(a_line_c1), ShowCreation(a_tip_c1)) + + text = TextMobject(r"Now, we have a vector $\beta_3(=\left[\begin{array}{c} 2\\2\\2 \end{array}\right])$") + text.set_color(GOLD_E) + text.scale(0.7) + self.add_fixed_in_frame_mobjects(text) + self.add_fixed_orientation_mobjects(axis[3]) + text.move_to(3*(DOWN+RIGHT)) + self.play(Write(text)) + self.wait() + self.play(FadeOut(text)) + + p_line1 = Line(start = ORIGIN,end = 2*RIGHT) + p_line1.set_color(GOLD_E) + p_tip1 = Polygon(RIGHT,0.8*RIGHT+0.2*DOWN,0.8*RIGHT+0.2*UP) + p_tip1.move_to(2*RIGHT) + p_tip1.set_opacity(1) + p_tip1.set_fill(GOLD_E) + p_tip1.set_color(GOLD_E) + + self.play(Transform(a_line_c1,p_line1),Transform(a_tip_c1,p_tip1)) + + text = TextMobject(r"Take projection of $\beta_3$ on $\alpha_1$") + text.scale(0.6) + text.set_color(GOLD_E) + self.add_fixed_in_frame_mobjects(text) + text.move_to(3*(DOWN+RIGHT)) + self.play(Write(text)) + self.wait() + self.play(FadeOut(text)) + + o_line1 = Line(start = 2*RIGHT,end = 2*UP+2*RIGHT+[0,0,2]) + o_line1.set_color(GREEN_E) + o_tip1 = Polygon(2*UP+2*RIGHT+[0,0,2],1.8*UP+2*RIGHT+[0,0,1.8]+0.2*RIGHT,1.8*UP+2*RIGHT+[0,0,1.8]-0.2*RIGHT) + o_tip1.set_opacity(1) + o_tip1.set_fill(GREEN_E) + o_tip1.set_color(GREEN_E) + + a_line1 = Line(start = ORIGIN,end = 2*UP+[0,0,2]) + a_line1.set_color(GREEN_E) + a_tip1 = Polygon(2*UP+[0,0,2],1.8*UP+[0,0,1.8]+0.2*RIGHT,1.8*UP+[0,0,1.8]-0.2*RIGHT) + a_tip1.set_opacity(1) + a_tip1.set_fill(GREEN_E) + a_tip1.set_color(GREEN_E) + + a_line1_c1 = Line(start = ORIGIN,end = 2*UP+[0,0,2]) + a_line1_c1.set_color(GREEN_E) + a_tip1_c1 = Polygon(2*UP+[0,0,2],1.8*UP+[0,0,1.8]+0.2*RIGHT,1.8*UP+[0,0,1.8]-0.2*RIGHT) + a_tip1_c1.set_opacity(1) + a_tip1_c1.set_fill(GREEN_E) + a_tip1_c1.set_color(GREEN_E) + + text = TextMobject(r"$\beta_3$-(projection of $\beta_3$ on $\alpha_1$)") + text.set_color(GREEN_E) + text.scale(0.6) + self.add_fixed_in_frame_mobjects(text) + text.move_to(3*(DOWN+RIGHT)) + self.play(Write(text)) + self.play(ShowCreation(o_line1), ShowCreation(o_tip1)) + self.wait(2) + self.play(FadeOut(a_line_c1), FadeOut(a_tip_c1), + FadeOut(a_line), FadeOut(a_tip), FadeOut(axis[3]), + Transform(o_line1,a_line1), Transform(o_tip1,a_tip1)) + + self.wait() + self.play(FadeOut(text)) + + p_arrow2 = Line(start = ORIGIN,end = 2*UP) + p_arrow2.set_color(GOLD_E) + p_tip2 = Polygon(2*UP,1.8*UP+0.2*RIGHT,1.8*UP+0.2*LEFT) + p_tip2.set_opacity(1) + p_tip2.set_fill(GOLD_E) + p_tip2.set_color(GOLD_E) + p_arrow2.set_color(GOLD_E) + + last_a = Line(start = 2*UP,end = [0,2,2]) + last_a.set_color(PURPLE_E) + last_a_tip = Polygon([0,0,2],[0,0,1.8]+0.2*RIGHT,[0,0,1.8]+0.2*LEFT) + last_a_tip.move_to([0,2,2]) + last_a_tip.set_opacity(1) + last_a_tip.set_fill(PURPLE_E) + last_a_tip.set_color(PURPLE_E) + + self.wait() + text = TextMobject(r"Take projection on $\alpha_2$") + text.scale(0.6) + text.set_color(GOLD_E) + self.add_fixed_in_frame_mobjects(text) + text.move_to(3*(DOWN+RIGHT)) + self.play(Write(text)) + self.play(Transform(a_line1_c1,p_arrow2),Transform(a_tip1_c1,p_tip2)) + self.wait() + self.play(FadeOut(text)) + + text = TextMobject(r"$\beta_3$-(projection of $\beta_3$ on $\alpha_1$ + projection of $\beta_3$ on $\alpha_2$)") + text.set_color(PURPLE_E) + text.scale(0.6) + self.add_fixed_in_frame_mobjects(text) + text.move_to(3*DOWN+3.5*RIGHT) + self.play(Write(text)) + self.play(ShowCreation(o_line1), ShowCreation(o_tip1)) + self.wait(2) + self.play(ShowCreation(last_a_tip), ShowCreation(last_a)) + self.wait() + self.play(FadeOut(text)) + + larrow3 = Line(start = ORIGIN,end = [0,0,2]) + larrow3.set_color(PURPLE_E) + ltip3 = Polygon([0,0,2],[0,0,1.8]+0.2*RIGHT,[0,0,1.8]+0.2*LEFT) + ltip3.set_opacity(1) + ltip3.set_fill(PURPLE_E) + ltip3.set_color(PURPLE_E) + self.wait() + self.play(FadeOut(o_line1), FadeOut(o_tip1), FadeOut(a_line1_c1), FadeOut(a_tip1_c1), Transform(last_a,larrow3), Transform(last_a_tip,ltip3)) + + text = TextMobject(r"Normalize, the vector") + text1 = TextMobject(r"$\beta_3$-(projection of $\beta_3$ on $\alpha_1$ + projection of $\beta_3$ on $\alpha_2$") + text.set_color(PURPLE_E) + text1.set_color(PURPLE_E) + text.scale(0.6) + text1.scale(0.6) + self.add_fixed_in_frame_mobjects(text) + self.add_fixed_in_frame_mobjects(text1) + text.move_to(3*DOWN+3*RIGHT) + text1.move_to(3.5*DOWN+3*RIGHT) + self.play(Write(text)) + self.play(Write(text1)) + + arrow3 = Line(start = ORIGIN,end = [0,0,1]) + arrow3.set_color(DARK_BLUE) + tip3 = Polygon([0,0,1],[0,0,0.8]-0.2*RIGHT,[0,0,0.8]-0.2*LEFT) + tip3.set_opacity(1) + tip3.set_fill(DARK_BLUE) + tip3.set_color(DARK_BLUE) + self.play(Transform(last_a,arrow3), Transform(last_a_tip,tip3)) + self.add_fixed_orientation_mobjects(axis[2]) + + self.wait() + self.play(FadeOut(text),FadeOut(text1)) + + text = TextMobject(r"These are the three orthonormal vectors $\alpha_1, \alpha_2, \alpha_3$") + text.set_color(DARK_BLUE) + self.add_fixed_in_frame_mobjects(text) + text.scale(0.6) + text.move_to(3*DOWN+3.5*RIGHT) + self.play(Write(text)) + + self.wait(3)
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file4_Non_Standard_Basis.py b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file4_Non_Standard_Basis.py new file mode 100644 index 0000000..6410a2c --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file4_Non_Standard_Basis.py @@ -0,0 +1,51 @@ +from manimlib.imports import * + +class NSB(ThreeDScene): + def construct(self): + + axes = ThreeDAxes(x_min = -4,x_max=4,y_min=-4,y_max=4,z_min=-4,z_max=4) + self.play(ShowCreation(axes)) + self.move_camera(phi=60*DEGREES,theta=45*DEGREES,run_time=3) + self.begin_ambient_camera_rotation(rate=0.5) + + matrix = [[0.577,0.577,0.577],[-0.577,0.577,0.577],[0.577,-0.577,0.577]] + + line1 = Line(start = ORIGIN,end = 1*RIGHT) + line1.set_color(DARK_BLUE) + tip1 = Polygon(RIGHT,0.9*RIGHT-0.1*DOWN,0.9*RIGHT-0.1*UP) + tip1.set_opacity(1) + tip1.set_fill(DARK_BLUE) + tip1.set_color(DARK_BLUE) + + arrow2 = Line(start = ORIGIN,end = 1*UP) + arrow2.set_color(DARK_BLUE) + tip2 = Polygon(UP,0.9*UP-0.1*RIGHT,0.9*UP-0.1*LEFT) + tip2.set_opacity(1) + tip2.set_fill(DARK_BLUE) + tip2.set_color(DARK_BLUE) + arrow2.set_color(DARK_BLUE) + + arrow3 = Line(start = ORIGIN,end = [0,0,1]) + arrow3.set_color(DARK_BLUE) + tip3 = Polygon([0,0,1],[0,0,0.9]-0.1*RIGHT,[0,0,0.9]-0.1*LEFT) + tip3.set_opacity(1) + tip3.set_fill(DARK_BLUE) + tip3.set_color(DARK_BLUE) + + line1.apply_matrix(matrix) + tip1.apply_matrix(matrix) + arrow2.apply_matrix(matrix) + tip2.apply_matrix(matrix) + arrow3.apply_matrix(matrix) + tip3.apply_matrix(matrix) + + self.play(ShowCreation(line1), ShowCreation(tip1), ShowCreation(arrow2), ShowCreation(tip2), ShowCreation(arrow3), ShowCreation(tip3)) + + text = TextMobject(r"This is also a set of Orthonormal Vectors") + text.set_color(DARK_BLUE) + self.add_fixed_in_frame_mobjects(text) + text.scale(0.6) + text.move_to(3*DOWN+3.5*RIGHT) + self.play(Write(text)) + + self.wait(7)
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file5.gif b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file5.gif Binary files differnew file mode 100644 index 0000000..2ce3577 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file5.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file6.gif b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file6.gif Binary files differnew file mode 100644 index 0000000..7cd7b3d --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file6.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file7.gif b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file7.gif Binary files differnew file mode 100644 index 0000000..19a13dd --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file7.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file8.gif b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file8.gif Binary files differnew file mode 100644 index 0000000..0ef4551 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Gram-Schmidt-Orthonormalization-Process/file8.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/README.md b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/README.md new file mode 100644 index 0000000..c286736 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/README.md @@ -0,0 +1,30 @@ +# Contributer: Archit Sangal +My Github Account : <a href="https://github.com/architsangal">architsangal</a> +<br/></br> + +## Sub-Topics Covered: ++ Linear Transformations (Linear Maps) + +#### Video 1: Visually understanding linear transformation(using grid) + + +#### Video 2: Linear Transformation when form 1 is given + + +#### Video 3: Matrix Representation Of Linear Transformation + + +#### Video 4: Understand Linear Transformations visually + + +#### Video 5: Uniform Scaling + + +#### Fig.1 Horizontal Shear + + +#### Fig.2 Vertical Shear + + +#### Video 6: Rotation by an angle of in anticlockwise direction +
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file.txt b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file.txt deleted file mode 100644 index cae98ce..0000000 --- a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file.txt +++ /dev/null @@ -1,3 +0,0 @@ -file 'text.mp4' -file 'LinearTransformation.mp4' -file 'NonLinearTransformation.mp4' diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file10.gif b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file10.gif Binary files differnew file mode 100644 index 0000000..d996130 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file10.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file11.gif b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file11.gif Binary files differnew file mode 100644 index 0000000..e9f4b08 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file11.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file12.gif b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file12.gif Binary files differnew file mode 100644 index 0000000..683f586 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file12.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file13.gif b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file13.gif Binary files differnew file mode 100644 index 0000000..ba6c156 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file13.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file14.gif b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file14.gif Binary files differnew file mode 100644 index 0000000..fd9bc7b --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file14.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file2_before_matrix.py b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file2_before_matrix.py new file mode 100755 index 0000000..96e456d --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file2_before_matrix.py @@ -0,0 +1,232 @@ +from manimlib.imports import * + +class Linear(GraphScene): + + CONFIG = { + "x_min": -5, + "x_max": 5, + "y_min": -5, + "y_max": 5, + "graph_origin": ORIGIN, + "x_labeled_nums": list(range(-5, 6)), + "y_labeled_nums": list(range(-5, 6)), + "x_axis_width": 7, + "y_axis_height": 7, + } + + def construct(self): + + XTD = self.x_axis_width/(self.x_max- self.x_min) + YTD = self.y_axis_height/(self.y_max- self.y_min) + + self.setup_axes(animate = True) + heading = TextMobject(r"$T(x,y) = T(x+2y,x-y)$") + heading.move_to(UP*3+LEFT*4) + heading.scale(0.7) + self.play(Write(heading)) + self.wait() + + before = TextMobject("Before Linear Transformation") + before.set_color(ORANGE) + before.move_to(3*UP+4*RIGHT) + before.scale(0.75) + dot1 = Dot().shift(self.graph_origin+1*XTD*RIGHT+1*YTD*UP) + dot2 = Dot().shift(self.graph_origin+2*XTD*RIGHT+1*YTD*UP) + dot1.set_color(ORANGE) + dot2.set_color(ORANGE) + p1 = TextMobject(r"$P_1$") + p1.scale(0.75) + p1.set_color(ORANGE) + p1.move_to(self.graph_origin+1*XTD*RIGHT+1.5*YTD*UP) + p2 = TextMobject(r"$P_2$") + p2.set_color(ORANGE) + p2.scale(0.75) + p2.move_to(self.graph_origin+2*XTD*RIGHT+1.5*YTD*UP) + + after = TextMobject("After applying Linear Transformation") + after.set_color(YELLOW) + after.move_to(3*UP+4.5*RIGHT) + after.scale(0.5) + dot3 = Dot().shift(self.graph_origin+3*XTD*RIGHT+0*YTD*UP) + dot4 = Dot().shift(self.graph_origin+4*XTD*RIGHT+1*YTD*UP) + dot3.set_color(YELLOW) + dot4.set_color(YELLOW) + p3 = TextMobject(r"$T(P_1)$") + p3.scale(0.7) + p3.set_color(YELLOW) + p3.move_to(self.graph_origin+3*XTD*RIGHT-1.1*YTD*UP) + p4 = TextMobject(r"$T(P_2)$") + p4.scale(0.7) + p4.set_color(YELLOW) + p4.move_to(self.graph_origin+4*XTD*RIGHT+1.5*YTD*UP) + + self.play(Write(before), ShowCreation(dot1), ShowCreation(dot2),Write(p1), Write(p2)) + self.wait(3) + self.play(Transform(before,after), Transform(dot1,dot3), Transform(dot2,dot4), Transform(p2,p4), Transform(p1,p3)) + self.wait(3) + + +class withgrid(LinearTransformationScene): + def construct(self): + + heading = TextMobject(r"Now, Imagine this happening for all the vectors") + heading.scale(0.5) + heading.move_to(UP*2.5+LEFT*4) + self.play(Write(heading)) + self.wait() + + before = TextMobject("Before Linear Transformation") + before.set_color(ORANGE) + before.move_to(3.5*UP+4*RIGHT) + before.scale(0.75) + dot1 = Dot().shift(1*RIGHT+1*UP) + dot2 = Dot().shift(2*RIGHT+1*UP) + dot1.set_color(ORANGE) + dot2.set_color(ORANGE) + + dot1_c = Dot(radius = 0.05).shift(1*RIGHT+1*UP) + dot2_c = Dot(radius = 0.05).shift(2*RIGHT+1*UP) + dot1_c.set_color(YELLOW) + dot2_c.set_color(YELLOW) + self.add_transformable_mobject(dot1_c) + self.add_transformable_mobject(dot2_c) + + p1 = TextMobject(r"$P_1$") + p1.scale(0.75) + p1.set_color(ORANGE) + p1.move_to(1*RIGHT+1.5*UP) + p2 = TextMobject(r"$P_2$") + p2.scale(0.75) + p2.set_color(ORANGE) + p2.move_to(2*RIGHT+1.5*UP) + + after = TextMobject("After applying Linear Transformation") + after.set_color(YELLOW) + after.move_to(3.5*UP+3.5*RIGHT) + after.scale(0.75) + dot3 = Dot().shift(3*RIGHT+0*UP) + dot4 = Dot().shift(4*RIGHT+1*UP) + dot3.set_color(YELLOW) + dot4.set_color(YELLOW) + p3 = TextMobject(r"$T(P_1)$") + p3.scale(0.75) + p3.set_color(YELLOW) + p3.move_to(3*RIGHT-0.6*UP) + p4 = TextMobject(r"$T(P_2)$") + p4.scale(0.75) + p4.set_color(YELLOW) + p4.move_to(4*RIGHT+1.5*UP) + + self.play(Write(before), ShowCreation(dot1), ShowCreation(dot2),Write(p1), Write(p2)) + self.wait(3) + matrix = [[1,2],[1,-1]] + dot1.set_color(GREY) + dot2.set_color(GREY) + self.play(FadeIn(dot1),FadeIn(dot2)) + self.apply_matrix(matrix) + self.play(Transform(before,after), Transform(p2,p4), Transform(p1,p3)) + self.play(Transform(before,after)) + self.wait(3) + + ending = TextMobject(r"$T(\left[\begin{array}{c}x \\ y\end{array}\right]) = \left[\begin{array}{c} x+2y \\ x-y\end{array}\right]$") + ending.move_to(UP*2+LEFT*4) + self.play(Transform(heading,ending)) + self.wait() + +from manimlib.imports import * +class ThreeDExplanation(ThreeDScene): + + def construct(self): + + text = TextMobject(r"$T(x,y) = (x+y,x-y,x+2y)$") + text.scale(0.75) + text.move_to(UP*2.5+LEFT*4) + self.add_fixed_in_frame_mobjects(text) + self.play(Write(text)) + self.wait() + + before = TextMobject("Before Linear Transformation") + self.add_fixed_in_frame_mobjects(before) + before.set_color(ORANGE) + before.move_to(3.5*UP+4*RIGHT) + before.scale(0.75) + + p1 = TextMobject(r"$P_1$") + p2 = TextMobject(r"$P_2$") + p3 = TextMobject(r"$P_3$") + p1.scale(0.75) + p2.scale(0.75) + p3.scale(0.75) + dot1 = Dot().shift(1*RIGHT+1*UP) + dot2 = Dot().shift(2*RIGHT+1*UP) + dot3 = Dot().shift(1*RIGHT+1*DOWN) + dot1.set_color(ORANGE) + dot2.set_color(ORANGE) + dot3.set_color(ORANGE) + self.play(ShowCreation(before)) + + p1.move_to(1*RIGHT+1*UP+[0,0,0.5]) + p2.move_to(2*RIGHT+1*UP+[0,0,0.5]) + p3.move_to(1*RIGHT-1*UP+[0,0,0.5]) + + dot1_c = Dot(radius = 0.05).shift(1*RIGHT+1*UP) + dot2_c = Dot(radius = 0.05).shift(0*RIGHT+2*UP) + dot3_c = Dot(radius = 0.05).shift(1*RIGHT-1*UP) + dot1_c.set_color(YELLOW) + dot2_c.set_color(YELLOW) + dot3_c.set_color(YELLOW) + + axes = ThreeDAxes(x_min = -7,x_max=7,y_min=-4,y_max=4,z_min=-4,z_max=4) + self.play(ShowCreation(axes)) + self.move_camera(distance = 100, phi=30*DEGREES,theta=45*DEGREES,run_time=3) + + self.begin_ambient_camera_rotation(rate=0.3) + self.wait(1) + self.stop_ambient_camera_rotation() + + plane = NumberPlane() + self.add_fixed_orientation_mobjects(p1) + self.add_fixed_orientation_mobjects(p2) + self.add_fixed_orientation_mobjects(p3) + self.play(ShowCreation(dot1),ShowCreation(dot3),ShowCreation(dot2),ShowCreation(plane)) + + self.play(FadeOut(before)) + after = TextMobject("After applying Linear Transformation") + self.add_fixed_in_frame_mobjects(after) + after.set_color(YELLOW) + after.move_to(3.5*UP+3.5*RIGHT) + after.scale(0.75) + + self.play(FadeOut(p1),FadeOut(p2),FadeOut(p3)) + matrix = [[1,1],[1,-1],[2,1]] + self.play(FadeOut(dot1),FadeOut(dot2),FadeOut(dot3),ApplyMethod(plane.apply_matrix,matrix),ApplyMethod(dot1_c.apply_matrix,matrix),ApplyMethod(dot3_c.apply_matrix,matrix),ApplyMethod(dot2_c.apply_matrix,matrix)) + + p4 = TextMobject(r"$T(P_1)$") + p5 = TextMobject(r"$T(P_2)$") + p6 = TextMobject(r"$T(P_3)$") + p4.scale(0.75) + p5.scale(0.75) + p6.scale(0.75) + p4.move_to(2*RIGHT+0*UP+[0,0,3.5]) + p5.move_to(2*RIGHT-2*UP+[0,0,2.5]) + p6.move_to(0*RIGHT+2*UP+[0,0,1.5]) + self.add_fixed_orientation_mobjects(p5) + self.add_fixed_orientation_mobjects(p4) + self.add_fixed_orientation_mobjects(p6) + + self.begin_ambient_camera_rotation(rate=0.3) + self.wait(3) + self.stop_ambient_camera_rotation() + + ending = TextMobject(r"$T(\left[\begin{array}{c}x \\ y\end{array}\right]) = \left[\begin{array}{c} x+y \\ x-y \\ x+2y \end{array}\right]$") + ending.scale(0.75) + ending.move_to(-UP*2+LEFT*4) + self.play(Transform(text,ending)) + self.add_fixed_in_frame_mobjects(ending) + + self.play(FadeOut(plane)) + self.wait(3) + + self.begin_ambient_camera_rotation(rate=0.5) + self.wait(5) + self.stop_ambient_camera_rotation() diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file3_square.py b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file3_square.py new file mode 100644 index 0000000..e828de4 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file3_square.py @@ -0,0 +1,246 @@ +from manimlib.imports import * + +class Linear(GraphScene): + CONFIG = { + "x_min": -5, + "x_max": 5, + "y_min": -5, + "y_max": 5, + "graph_origin": ORIGIN, + "x_labeled_nums": list(range(-5, 6)), + "y_labeled_nums": list(range(-5, 6)), + "x_axis_width": 7, + "y_axis_height": 7, + } + def construct(self): + + text = TextMobject("T(x,y) = T(x+y,y)") + text.scale(0.75) + text.set_color(PURPLE) + text.move_to(3*UP+5*LEFT) + self.play(Write(text)) + + XTD = self.x_axis_width/(self.x_max- self.x_min) + YTD = self.y_axis_height/(self.y_max- self.y_min) + + self.setup_axes(animate = True) + + text1 = TextMobject("Before Linear Transformation") + text1.scale(0.6) + text1.move_to(UP*3+3*RIGHT) + + a = TextMobject("(1,1)") + b = TextMobject("(3,1)") + c = TextMobject("(3,2)") + d = TextMobject("(1,2)") + a.scale(0.5) + b.scale(0.5) + c.scale(0.5) + d.scale(0.5) + a.move_to(self.graph_origin+0.6*UP+0.6*RIGHT) + b.move_to(self.graph_origin+0.6*UP+3.4*RIGHT) + c.move_to(self.graph_origin+2.4*UP+3.4*RIGHT) + d.move_to(self.graph_origin+2.6*UP+0.6*RIGHT) + + square = Polygon(self.graph_origin+UP+RIGHT,self.graph_origin+UP+3*RIGHT,self.graph_origin+2*UP+3*RIGHT,self.graph_origin+2*UP+RIGHT) + + self.play(Write(text1), Write(a), Write(b), Write(c), Write(d), ShowCreation(square)) + self.wait(2) + self.play(FadeOut(text1), FadeOut(a), FadeOut(b), FadeOut(c), FadeOut(d), ApplyMethod(square.apply_matrix,[[1,1],[0,1]])) + + a = TextMobject("(2,1)") + b = TextMobject("(4,1)") + c = TextMobject("(3,2)") + d = TextMobject("(5,2)") + a.scale(0.5) + b.scale(0.5) + c.scale(0.5) + d.scale(0.5) + a.move_to(self.graph_origin+0.6*UP+1.6*RIGHT) + b.move_to(self.graph_origin+0.6*UP+4.4*RIGHT) + d.move_to(self.graph_origin+2.4*UP+5.4*RIGHT) + c.move_to(self.graph_origin+2.4*UP+2.6*RIGHT) + + text1 = TextMobject("After Linear Transformation") + text1.scale(0.6) + text1.move_to(UP*3+3*RIGHT) + + self.play(Write(text1), Write(a), Write(b), Write(c), Write(d)) + + self.wait(2) + +class grid(LinearTransformationScene): + def construct(self): + + text = TextMobject("Now, consider all the vectors.") + text.scale(0.75) + text.set_color(PURPLE) + text.move_to(2.5*UP+3*LEFT) + self.play(Write(text)) + + text1 = TextMobject("Before Linear Transformation") + text1.scale(0.6) + text1.move_to(UP*3.5+3.5*RIGHT) + + square = Polygon(UP+RIGHT,UP+3*RIGHT,2*UP+3*RIGHT,2*UP+RIGHT) + square.set_color(YELLOW) + + self.play(Write(text1), ShowCreation(square)) + self.wait(2) + self.play(FadeOut(text1)) + self.add_transformable_mobject(square) + + text1 = TextMobject("After Linear Transformation") + text1.scale(0.6) + text1.move_to(UP*3.5+3.5*RIGHT) + + matrix = [[1,1],[0,1]] + + self.apply_matrix(matrix) + self.play(Write(text1)) + + self.wait() + +class grid2(LinearTransformationScene): + CONFIG = { + "include_background_plane": True, + "include_foreground_plane": False, + "show_coordinates": True, + "show_basis_vectors": True, + "basis_vector_stroke_width": 3, + "i_hat_color": X_COLOR, + "j_hat_color": Y_COLOR, + "leave_ghost_vectors": True, + } + + def construct(self): + + text = TextMobject("Now, let us focus only on the standard basis") + text.scale(0.7) + text.set_color(PURPLE) + text.move_to(2.5*UP+3.5*LEFT) + self.play(Write(text)) + + text1 = TextMobject("Before Linear Transformation") + text1.scale(0.6) + text1.move_to(UP*3.5+3.5*RIGHT) + + square = Polygon(UP+RIGHT,UP+3*RIGHT,2*UP+3*RIGHT,2*UP+RIGHT) + square.set_color(YELLOW) + + self.play(Write(text1), ShowCreation(square)) + self.wait(2) + self.play(FadeOut(text1)) + self.add_transformable_mobject(square) + + text1 = TextMobject("After Linear Transformation") + text1.scale(0.6) + text1.move_to(UP*3.5+3.5*RIGHT) + + matrix = [[1,1],[0,1]] + + self.apply_matrix(matrix) + self.play(Write(text1)) + + self.play(FadeOut(square), FadeOut(text1)) + + cor_x = TextMobject("(1,0)") + cor_y = TextMobject("(1,1)") + cor_x.scale(0.65) + cor_y.scale(0.65) + cor_y.move_to(1.25*RIGHT+1.5*UP) + cor_x.move_to(0.75*RIGHT-0.5*UP) + cor_x.set_color(GREEN) + cor_y.set_color(RED) + + x_cor = TextMobject(r"$\left[\begin{array}{c} 1\\0\end{array}\right]$") + x_cor.set_color(GREEN) + x_cor.scale(0.5) + y_cor = TextMobject(r"$\left[\begin{array}{c} 1\\1\end{array}\right]$") + x_cor.move_to(0.75*RIGHT-0.5*UP) + y_cor.move_to(1.25*RIGHT+1.5*UP) + y_cor.set_color(RED) + y_cor.scale(0.5) + + text1 = TextMobject(r"$T(\left[\begin{array}{c} x\\y \end{array}\right]) = $",r"$\left[\begin{array}{c} x+y\\y \end{array}\right]$") + text1.scale(0.7) + text1.set_color(PURPLE) + text1.move_to(1.5*UP+3*LEFT) + + text = TextMobject(r"$T(x,y) = (x+y,y)$") + text.scale(0.6) + text.set_color(PURPLE) + text.move_to(1.5*UP+3*LEFT) + + self.play(FadeIn(text),FadeIn(cor_x), FadeIn(cor_y)) + self.wait() + + self.play(Transform(text,text1), Transform(cor_x,x_cor), Transform(cor_y,y_cor)) + + text3 = TextMobject(r"$\left[\begin{array}{c} x+y\\y \end{array}\right]$") + text3.scale(0.7) + text3.set_color(PURPLE) + text3.move_to(1.5*DOWN+5*LEFT) + + equal = TextMobject("=") + equal.move_to(1.5*DOWN+3.5*LEFT) + + text3 = TextMobject("[") + text4 = TextMobject(r"$\begin{array}{c} (1)x\\(0)x \end{array}$") + text5 = TextMobject(r"$\begin{array}{c} + \\ + \end{array}$") + text6 = TextMobject(r"$\begin{array}{c} (1)y\\(1)y \end{array}$") + text7 = TextMobject("]") + text3.scale(2) + text4.scale(0.7) + text5.scale(0.7) + text6.scale(0.7) + text7.scale(2) + text4.set_color(GREEN) + text5.set_color(PURPLE) + text6.set_color(RED) + text3.move_to(1.5*DOWN+3*LEFT) + text4.move_to(1.5*DOWN+2.5*LEFT) + text5.move_to(1.5*DOWN+2*LEFT) + text6.move_to(1.5*DOWN+1.5*LEFT) + text7.move_to(1.5*DOWN+1*LEFT) + + text1[1].scale(1.2) + self.play(FadeOut(text1[0]), ApplyMethod(text1[1].move_to,1.5*DOWN+5*LEFT), FadeIn(text3), FadeIn(equal), FadeIn(text4), FadeIn(text5), FadeIn(text6), FadeIn(text7)) + + self.wait() + self.play(FadeOut(text1[1])) + + self.play(ApplyMethod(text3.move_to,1.5*DOWN+6*LEFT), + ApplyMethod(text4.move_to,1.5*DOWN+5.5*LEFT), + ApplyMethod(text5.move_to,1.5*DOWN+5*LEFT), + ApplyMethod(text6.move_to,1.5*DOWN+4.5*LEFT), + ApplyMethod(text7.move_to,1.5*DOWN+4*LEFT)) + + text10 = TextMobject("[") + text11 = TextMobject(r"$\begin{array}{c} 1\\0 \end{array}$") + text13 = TextMobject(r"$\begin{array}{c} 1\\1 \end{array}$") + text14 = TextMobject("]") + text10.scale(2) + text11.scale(0.7) + text13.scale(0.7) + text14.scale(2) + text11.set_color(GREEN) + text13.set_color(RED) + text10.move_to(1.5*DOWN+3*LEFT) + text11.move_to(1.5*DOWN+2.75*LEFT) + text13.move_to(1.5*DOWN+2.25*LEFT) + text14.move_to(1.5*DOWN+2*LEFT) + + self.play(FadeIn(text10), Transform(x_cor,text11), Transform(y_cor,text13), FadeIn(text14)) + + text15 = TextMobject(r"$\left[\begin{array}{c} x\\y \end{array}\right]$") + text15.scale(0.7) + text15.set_color(PURPLE) + text15.move_to(1.5*DOWN+1.5*LEFT) + + self.play(FadeIn(text15)) + self.play(FadeOut(text3), FadeOut(text4), FadeOut(text5), FadeOut(text7), FadeOut(text6)) + + text1[0].scale(1.2) + self.play(ApplyMethod(text1[0].move_to,1.5*DOWN+4.5*LEFT), FadeOut(equal)) + self.wait(2)
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file2_Understand_Linear_Transformations_visually.py b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file4_Understand_Linear_Transformations_visually.py index 577032d..577032d 100644 --- a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file2_Understand_Linear_Transformations_visually.py +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file4_Understand_Linear_Transformations_visually.py diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file3_Uniform_Scaling.py b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file5_Uniform_Scaling.py index a7856a5..a7856a5 100644 --- a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file3_Uniform_Scaling.py +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file5_Uniform_Scaling.py diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file4_Horizontal_Shear.py b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file6_Horizontal_Shear.py index 91f098e..91f098e 100644 --- a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file4_Horizontal_Shear.py +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file6_Horizontal_Shear.py diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file4_Horizontal_Shear_gif.gif b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file6_Horizontal_Shear_gif.gif Binary files differindex 9bef1b6..9bef1b6 100644 --- a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file4_Horizontal_Shear_gif.gif +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file6_Horizontal_Shear_gif.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file5_Vertical_Shear.py b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file7_Vertical_Shear.py index 718e4e0..718e4e0 100644 --- a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file5_Vertical_Shear.py +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file7_Vertical_Shear.py diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file5_Vertical_Shear_gif.gif b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file7_Vertical_Shear_gif.gif Binary files differindex 7ca323f..7ca323f 100644 --- a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file5_Vertical_Shear_gif.gif +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file7_Vertical_Shear_gif.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file6_linear_transformation.py b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file8_linear_transformation.py index 01a0cef..01a0cef 100755 --- a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file6_linear_transformation.py +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file8_linear_transformation.py diff --git a/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file9.gif b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file9.gif Binary files differnew file mode 100644 index 0000000..017e0c7 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Linear-Transformations-(Linear-Maps)/file9.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Orthonormal Basis/file1_orthogonal.py b/FSF-2020/linear-algebra/linear-transformations/Orthonormal Basis/file1_orthogonal.py deleted file mode 100755 index b400f93..0000000 --- a/FSF-2020/linear-algebra/linear-transformations/Orthonormal Basis/file1_orthogonal.py +++ /dev/null @@ -1,34 +0,0 @@ -from manimlib.imports import *
-
-class Orthogonal(ThreeDScene):
- def construct(self):
- axes = ThreeDAxes()
- self.play(ShowCreation(axes))
- self.move_camera(phi=30*DEGREES,theta=-45*DEGREES,run_time=3)
- line1 = Line(start = ORIGIN,end = -3*LEFT)
- line1.set_color(DARK_BLUE)
- tip1 = Polygon(-LEFT,-0.8*LEFT-0.2*DOWN,-0.8*LEFT-0.2*UP)
- tip1.move_to(-3*LEFT)
- tip1.set_opacity(1)
- tip1.set_fill(DARK_BLUE)
- tip1.set_color(DARK_BLUE)
-
- arrow2 = Line(start = ORIGIN,end = -3*UP)
- arrow2.set_color(DARK_BLUE)
- tip2 = Polygon(DOWN,0.8*DOWN-0.2*RIGHT,0.8*DOWN-0.2*LEFT)
- tip2.move_to(3*DOWN)
- tip2.set_opacity(1)
- tip2.set_fill(DARK_BLUE)
- tip2.set_color(DARK_BLUE)
- arrow2.set_color(DARK_BLUE)
-
- arrow3 = Line(start = ORIGIN,end = [0,0,3])
- arrow3.set_color(DARK_BLUE)
- tip3 = Polygon([0,0,3],[0,0,2.8]-0.2*RIGHT,[0,0,2.8]-0.2*LEFT)
- tip3.set_opacity(1)
- tip3.set_fill(DARK_BLUE)
- tip3.set_color(DARK_BLUE)
-
- self.play(ShowCreation(line1), ShowCreation(tip1), ShowCreation(arrow2), ShowCreation(tip2), ShowCreation(arrow3), ShowCreation(tip3))
-
- self.wait()
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Orthonormal Basis/file2_OrthonormalBasis.py b/FSF-2020/linear-algebra/linear-transformations/Orthonormal Basis/file2_OrthonormalBasis.py deleted file mode 100644 index 0a28f22..0000000 --- a/FSF-2020/linear-algebra/linear-transformations/Orthonormal Basis/file2_OrthonormalBasis.py +++ /dev/null @@ -1,82 +0,0 @@ -from manimlib.imports import * -class OrthonormalBasis(GraphScene): - CONFIG = { - "x_min" : -6, - "x_max" : 6, - "y_min" : -4, - "y_max" : 4, - "graph_origin" : ORIGIN , -} - - def construct(self): - self.setup_axes(animate=True) - - XTD = self.x_axis_width/(self.x_max-self.x_min) - YTD = self.y_axis_height/(self.y_max-self.y_min) - - arrow1 = Arrow(start = ORIGIN,end = 0.707*YTD*UP+0.707*XTD*RIGHT) - arrow1.scale(2.25) - arrow1.set_color(DARK_BLUE) - - arrow2 = Arrow(start = ORIGIN,end = 0.707*YTD*UP+0.707*XTD*LEFT) - arrow2.scale(2.25) - arrow2.set_color(DARK_BLUE) - - square = Polygon(UP*0.4*YTD,0.2*(YTD*UP+XTD*RIGHT),ORIGIN,0.2*(YTD*UP+XTD*LEFT)) - square.set_color(DARK_BLUE) - self.play(ShowCreation(arrow2), ShowCreation(arrow1), ShowCreation(square)) - - ortho = TextMobject("Orthonormal Vectors") - ortho.scale(0.75) - ortho.move_to(DOWN+3*RIGHT) - self.play(Write(ortho)) - self.wait() - self.play(FadeOut(ortho)) - - arrow3 = Arrow(start = ORIGIN,end = YTD*3*UP+XTD*LEFT) - arrow3.scale(1.25) - arrow3.set_color(GOLD_E) - self.play(ShowCreation(arrow3)) - - arrow4 = Arrow(start = ORIGIN,end = YTD*UP+XTD*RIGHT) - arrow4.scale(1.8) - arrow4.set_color(GOLD_A) - - arrow5 = Arrow(start = ORIGIN,end = 2*YTD*UP-2*XTD*RIGHT) - arrow5.scale(1.3) - arrow5.set_color(GOLD_A) - - self.play(ShowCreation(arrow5), ShowCreation(arrow4)) - - self.wait() - - self.play(FadeOut(arrow1), FadeOut(arrow2), FadeOut(square)) - - self.wait() - - text1 = TextMobject(r"$<v,v_1> v_1$") - text1.move_to(UP+2*RIGHT) - text1.scale(0.75) - text2 = TextMobject(r"$<v,v_2> v_2$") - text2.move_to(UP+3*LEFT) - text2.scale(0.75) - - text3 = TextMobject("v") - text3.move_to(YTD*3.5*UP+XTD*1.5*LEFT) - - self.play(Write(text1), Write(text2), Write(text3)) - self.wait() - - line1 = DashedLine(start = YTD*UP+XTD*RIGHT, end = YTD*3*UP+XTD*1*LEFT) - line2 = DashedLine(start = YTD*2*UP+XTD*2*LEFT, end = YTD*3*UP+XTD*1*LEFT) - self.play(ShowCreation(line1),ShowCreation(line2)) - - self.wait() - - text = TextMobject(r"$v$ is the sum of projections","on the orthonormal vectors") - text[0].move_to(DOWN+3.2*RIGHT) - text[1].move_to(1.5*DOWN+3.2*RIGHT) - self.play(Write(text)) - self.wait(2) - self.play(FadeOut(arrow3), FadeOut(arrow4), FadeOut(arrow5), FadeOut(text1), FadeOut(text2), FadeOut(text3), FadeOut(self.axes), FadeOut(line1), FadeOut(line2)) - self.play(FadeOut(text)) diff --git a/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/README.md b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/README.md new file mode 100644 index 0000000..55aba66 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/README.md @@ -0,0 +1,15 @@ +# Contributer: Archit Sangal +My Github Account : <a href="https://github.com/architsangal">architsangal</a> +<br/></br> + +## Sub-Topics Covered: ++ Orthonormal Bases + +#### Video 1: Example of Orthonormal bases + + +#### Video 2: Adding the projections of a vector on orthonormal basis will produce the same vector + + +#### Video 3: Relating the example and the property +
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file1_orthogonal.py b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file1_orthogonal.py new file mode 100755 index 0000000..a5d96f5 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file1_orthogonal.py @@ -0,0 +1,40 @@ +from manimlib.imports import *
+
+class Orthogonal(ThreeDScene):
+ def construct(self):
+ axes = ThreeDAxes()
+ self.play(ShowCreation(axes))
+ self.move_camera(phi=60*DEGREES,theta=45*DEGREES,run_time=3)
+
+ text = TextMobject(r"$\hat{i}$",r"$\hat{j}$",r"$\hat{k}$")
+ text[0].move_to(0.7*DOWN+0.8*LEFT)
+ text[1].move_to(0.75*DOWN+0.7*RIGHT)
+ text[2].move_to(0.75*UP+0.4*RIGHT)
+ self.add_fixed_in_frame_mobjects(text)
+ self.play(Write(text))
+
+ line1 = Line(start = ORIGIN,end = RIGHT)
+ line1.set_color(DARK_BLUE)
+ tip1 = Polygon(-0.95*LEFT,-0.8*LEFT-0.1*DOWN,-0.8*LEFT-0.1*UP)
+ tip1.set_opacity(1)
+ tip1.set_fill(DARK_BLUE)
+ tip1.set_color(DARK_BLUE)
+
+ arrow2 = Line(start = ORIGIN,end = UP)
+ arrow2.set_color(DARK_BLUE)
+ tip2 = Polygon(0.95*UP,0.8*UP-0.1*RIGHT,0.8*UP-0.1*LEFT)
+ tip2.set_opacity(1)
+ tip2.set_fill(DARK_BLUE)
+ tip2.set_color(DARK_BLUE)
+ arrow2.set_color(DARK_BLUE)
+
+ arrow3 = Line(start = ORIGIN,end = [0,0,1])
+ arrow3.set_color(DARK_BLUE)
+ tip3 = Polygon([0,0,0.95],[0,0,0.8]-0.1*RIGHT,[0,0,0.8]-0.1*LEFT)
+ tip3.set_opacity(1)
+ tip3.set_fill(DARK_BLUE)
+ tip3.set_color(DARK_BLUE)
+
+ self.play(ShowCreation(line1), ShowCreation(tip1), ShowCreation(arrow2), ShowCreation(tip2), ShowCreation(arrow3), ShowCreation(tip3))
+
+ self.wait()
diff --git a/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file2_sum_of_projections_part1.py b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file2_sum_of_projections_part1.py new file mode 100755 index 0000000..81a0888 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file2_sum_of_projections_part1.py @@ -0,0 +1,133 @@ +from manimlib.imports import *
+class LinearTrans(LinearTransformationScene):
+ CONFIG = {
+ "show_basis_vectors": True,
+ "basis_vector_stroke_width": 1,
+ "leave_ghost_vectors": False,
+ "show_coordinates": True,
+ }
+
+ def construct(self):
+
+ self.setup()
+
+ matrix = [[0.6,-0.8],[0.8,0.6]]
+ self.apply_matrix(matrix)
+
+ self.wait(2)
+ orthonormal = TextMobject(r"These are 2 orthonormal vectors($v_1$ and $v_2$)")
+ orthonormal.scale(0.7)
+ orthonormal.move_to(DOWN+LEFT*3.5)
+ orthonormal.add_background_rectangle()
+ v1 = TextMobject(r"$v_1$")
+ v1.scale(0.75)
+ v1.set_color(X_COLOR)
+ v1.move_to(0.75*UP+RIGHT)
+ v1.add_background_rectangle()
+ v2 = TextMobject(r"$v_2$")
+ v2.scale(0.75)
+ v2.set_color(Y_COLOR)
+ v2.move_to(0.75*UP+LEFT*1.25)
+ v2.add_background_rectangle()
+ self.play(Write(orthonormal))
+ self.play(Write(v1),Write(v2))
+ self.wait()
+ self.play(FadeOut(orthonormal), FadeOut(v1), FadeOut(v2))
+
+ arrow = Arrow(start = ORIGIN,end = 3*RIGHT+UP)
+ arrow.scale(1.2)
+ arrow.set_color(BLUE)
+ arrow.apply_matrix(matrix)
+ text3 = TextMobject("v")
+ text3.move_to(3.2*UP+1.2*RIGHT)
+ text3.add_background_rectangle()
+ self.play(ShowCreation(arrow),Write(text3))
+ self.wait()
+ v_cor = TextMobject("(1,3)")
+ v_cor.move_to(3.2*UP+1.3*RIGHT)
+ v_cor.set_color(BLUE)
+ v_cor.scale(0.75)
+ v_cor.add_background_rectangle()
+ self.play(Transform(text3,v_cor))
+
+ line1 = DashedLine(start = 1*UP+3*RIGHT, end = 3*RIGHT)
+ line2 = DashedLine(start = 1*UP+3*RIGHT, end = UP)
+ line1.apply_matrix(matrix)
+ line2.apply_matrix(matrix)
+ self.play(ShowCreation(line1),ShowCreation(line2),run_time = 2)
+
+ v1 = Arrow(start = ORIGIN,end = 3*RIGHT+UP)
+ v1.scale(1.2)
+ v1.set_color(BLUE)
+ v1.apply_matrix(matrix)
+ arrow1 = Arrow(start = ORIGIN,end = 3*RIGHT)
+ arrow1.scale(1.2)
+ arrow1.set_color("#6B8E23")
+ arrow1.apply_matrix(matrix)
+ self.play(Transform(v1,arrow1))
+ v1_cor = TextMobject(r"$<v,v_1> v_1$")
+ v1_cor.move_to(2.5*UP+3*RIGHT)
+ v1_cor.scale(0.75)
+ v1_cor.add_background_rectangle()
+ self.play(Write(v1_cor))
+ self.wait(0.5)
+ text1 = TextMobject(r"(1.8,2.4)")
+ text1.move_to(2.1*UP+2.5*RIGHT)
+ text1.scale(0.75)
+ text1.set_color("#6B8E23")
+ text1.add_background_rectangle()
+ self.play(Transform(v1_cor,text1))
+
+ v2 = Arrow(start = ORIGIN,end = 3*RIGHT+UP)
+ v2.scale(1.2)
+ v2.set_color("#8b0000")
+ v2.apply_matrix(matrix)
+ arrow2 = Arrow(start = ORIGIN,end = UP)
+ arrow2.scale(2.1)
+ arrow2.set_color("#8b0000")
+ arrow2.apply_matrix(matrix)
+ self.wait(0.5)
+ self.play(Transform(v2,arrow2))
+ self.wait(0.5)
+ v2_cor = TextMobject(r"$<v,v_2> v_2$")
+ v2_cor.move_to(0.75*UP+2.5*LEFT)
+ v2_cor.scale(0.75)
+ v2_cor.add_background_rectangle()
+ self.play(Write(v2_cor))
+ self.wait(0.5)
+ text2 = TextMobject(r"(-0.8,0.6)")
+ text2.move_to(0.75*UP+1.75*LEFT)
+ text2.scale(0.75)
+ text2.set_color("#8b0000")
+ text2.add_background_rectangle()
+ self.play(Transform(v2_cor,text2))
+
+ self.wait()
+
+ self.play(ApplyMethod(v2.move_to,1.4*RIGHT+2.7*UP),FadeOut(v1_cor),FadeOut(v2_cor),FadeOut(v_cor))
+
+ self.wait()
+
+ ending = TextMobject(r"$v = <v,v_1> v_1 + <v,v_2> v_2$")
+ ending.scale(0.7)
+ ending.move_to(DOWN)
+ ending.add_background_rectangle()
+ self.play(Write(ending))
+ self.wait()
+ self.play(FadeOut(ending))
+
+ ending = TextMobject(r"$\left[ \begin{array} {c} 1\\ 3 \end{array}\right] = \left[ \begin{array} {c}1.8 \\ 2.4 \end{array}\right] + \left[ \begin{array} {c} -0.8\\ 0.6 \end{array}\right]$")
+ ending.scale(0.7)
+ ending.move_to(DOWN)
+ ending.add_background_rectangle()
+ self.play(Write(ending))
+ self.wait()
+ self.play(FadeOut(ending))
+
+ ending = TextMobject(r"$v$ is the sum of projections on the orthonormal vectors")
+ ending.scale(0.7)
+ ending.move_to(DOWN)
+ ending.add_background_rectangle()
+ self.play(Write(ending))
+ self.wait()
+ self.play(FadeOut(ending))
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file3_sum_of_projections_part2.py b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file3_sum_of_projections_part2.py new file mode 100644 index 0000000..9d25192 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file3_sum_of_projections_part2.py @@ -0,0 +1,173 @@ +from manimlib.imports import * +class ThreeDExplanation(ThreeDScene): + + def construct(self): + + text = TextMobject("Let us consider the example discussed above again. These are the things we know:-") + text.scale(0.75) + self.add_fixed_in_frame_mobjects(text) + text.move_to(3*UP) + self.play(Write(text)) + self.wait(2) + basis = TextMobject(r"Set of Orthonormal Basis - $\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\\0\end{array}\right),\left(\begin{array}{c}\frac{-1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\\0\end{array}\right),\left(\begin{array}{c}0\\0\\1\end{array}\right)$") + basis.scale(0.75) + basis.move_to(UP*1.5) + self.play(Write(basis)) + v = TextMobject(r"$v_1$",r"$v_2$",r"$v_3$") + v[0].move_to(UP*0.5+RIGHT*0.75) + v[1].move_to(UP*0.5+RIGHT*2.5) + v[2].move_to(UP*0.5+RIGHT*4) + eq = TextMobject(r"$v = \left(\begin{array}{c}3\\4\\5\end{array}\right)$") + eq1 = TextMobject(r"$<v,v_1> = \frac{3}{\sqrt{2}} + \frac{4}{\sqrt{2}} + 0 = \frac{7}{\sqrt{2}}$") + eq2 = TextMobject(r"$<v,v_2> = \frac{-3}{\sqrt{2}} + \frac{4}{\sqrt{2}} + 0 =\frac{1}{\sqrt{2}}$") + eq3 = TextMobject(r"$<v,v_3> = 0 + 0 + 5 =5$") + eq.move_to(4*LEFT+DOWN) + eq1.move_to(0.5*DOWN+2*RIGHT) + eq2.move_to(1.5*DOWN+2*RIGHT) + eq3.move_to(2.5*DOWN+2*RIGHT) + self.play(Write(v)) + self.play(Write(eq)) + self.play(Write(eq1)) + self.play(Write(eq2)) + self.play(Write(eq3)) + self.wait() + self.play(FadeOut(text), FadeOut(basis), FadeOut(eq), FadeOut(v), FadeOut(eq1), FadeOut(eq2), FadeOut(eq3)) + self.wait() + + text = TextMobject("These are the 3 mutually orthonormal basis of the set(", r"$v_1$, ", r"$v_2$, ", r"$v_3$",")") + text[1].set_color(DARK_BLUE) + text[2].set_color(RED) + text[3].set_color(YELLOW) + text.scale(0.75) + self.add_fixed_in_frame_mobjects(text) + text.move_to(3*DOWN) + self.play(Write(text)) + self.wait() + + axes = ThreeDAxes(x_min = -9,x_max=9,y_min=-9,y_max=9,z_min=-9,z_max=9) + self.play(ShowCreation(axes)) + self.move_camera(distance = 100, phi=30*DEGREES,theta=45*DEGREES,run_time=3) + self.begin_ambient_camera_rotation(rate=0.3) + + dashedline1 = DashedLine(start = -12*(UP+RIGHT), end = 12*(UP+RIGHT)) + dashedline2 = DashedLine(start = -12*(UP+LEFT), end = 12*(UP+LEFT)) + dashedline3 = DashedLine(start = 4*UP+3*RIGHT+[0,0,5], end = 3.5*UP+3.5*RIGHT) + dashedline4 = DashedLine(start = 4*UP+3*RIGHT+[0,0,5], end = 0.5*UP+0.5*LEFT) + dashedline5 = DashedLine(start = 4*UP+3*RIGHT+[0,0,5], end = [0,0,5]) + + self.play(ShowCreation(dashedline1), ShowCreation(dashedline2)) + + line1 = Line(start = ORIGIN,end = 0.707*RIGHT + 0.707*UP) + line1.set_color(DARK_BLUE) + tip1 = Polygon(0.707*RIGHT + 0.707*UP, 0.707*RIGHT + 0.607*UP, 0.607*RIGHT + 0.707*UP) + tip1.set_opacity(1) + tip1.set_fill(DARK_BLUE) + tip1.set_color(DARK_BLUE) + self.play(ShowCreation(line1), ShowCreation(tip1)) + + line2 = Line(start = ORIGIN,end = 0.707*LEFT + 0.707*UP) + line2.set_color(RED) + tip2 = Polygon(0.707*LEFT + 0.707*UP, 0.707*LEFT + 0.607*UP, 0.607*LEFT + 0.707*UP) + tip2.set_opacity(1) + tip2.set_fill(RED) + tip2.set_color(RED) + + self.play(ShowCreation(line2), ShowCreation(tip2)) + + line3 = Line(start = ORIGIN,end = [0,0,1]) + line3.set_color(YELLOW) + tip3 = Polygon([0,0,1],[0,0,0.8]-0.2*RIGHT,[0,0,0.8]-0.2*LEFT) + tip3.set_opacity(1) + tip3.set_fill(YELLOW) + tip3.set_color(YELLOW) + self.play(ShowCreation(line3), ShowCreation(tip3)) + self.wait() + + self.play(FadeOut(text)) + + text = TextMobject("Take the projection of ", r"$v$", " on the mutually orthonormal vectors") + text[1].set_color(GOLD_E) + text.scale(0.75) + self.add_fixed_in_frame_mobjects(text) + text.move_to(3*DOWN) + self.play(Write(text)) + self.wait(2) + + a_line = Line(start = ORIGIN,end = 4*UP+3*RIGHT+[0,0,5]) + a_line.set_color(GOLD_E) + a_tip = Polygon(4*UP+3*RIGHT+[0,0,5],3.6*UP+2.7*RIGHT+[0,0,4.5]+0.1*UP+0.1*LEFT,3.6*UP+2.7*RIGHT+[0,0,4.5]+0.1*DOWN+0.1*RIGHT) + a_tip.set_opacity(1) + a_tip.set_fill(GOLD_E) + a_tip.set_color(GOLD_E) + + self.play(ShowCreation(a_line), ShowCreation(a_tip)) + self.wait(9) + self.play(ShowCreation(dashedline3),ShowCreation(dashedline4),ShowCreation(dashedline5)) + self.wait(6) + + pv1 = Line(start = ORIGIN,end = 4*UP+3*RIGHT+[0,0,5]) + pv1.set_color(GOLD_E) + pv1tip = Polygon(4*UP+3*RIGHT+[0,0,5],3.6*UP+2.7*RIGHT+[0,0,4.5]+0.1*UP+0.1*LEFT,3.6*UP+2.7*RIGHT+[0,0,4.5]+0.1*DOWN+0.1*RIGHT) + pv1tip.set_opacity(1) + pv1tip.set_fill(GOLD_E) + pv1tip.set_color(GOLD_E) + + v1_p = Line(start = ORIGIN,end = 3.5*RIGHT + 3.5*UP) + v1_p.set_color(BLUE_E) + v1_p_tip = Polygon(3.5*RIGHT + 3.5*UP, 3.5*RIGHT + 3.4*UP, 3.4*RIGHT + 3.5*UP) + v1_p_tip.set_opacity(1) + v1_p_tip.set_fill(BLUE_E) + v1_p_tip.set_color(BLUE_E) + + pv2 = Line(start = ORIGIN,end = 4*UP+3*RIGHT+[0,0,5]) + pv2.set_color(GOLD_E) + pv2tip = Polygon(4*UP+3*RIGHT+[0,0,5],3.6*UP+2.7*RIGHT+[0,0,4.5]+0.1*UP+0.1*LEFT,3.6*UP+2.7*RIGHT+[0,0,4.5]+0.1*DOWN+0.1*RIGHT) + pv2tip.set_opacity(1) + pv2tip.set_fill(GOLD_E) + pv2tip.set_color(GOLD_E) + + v2_p = Line(start = ORIGIN,end = 0.5*LEFT + 0.5*UP) + v2_p.set_color(RED_E) + v2_p_tip = Polygon(0.5*LEFT + 0.5*UP, 0.5*LEFT + 0.4*UP, 0.4*LEFT + 0.5*UP) + v2_p_tip.set_opacity(1) + v2_p_tip.set_fill(RED_E) + v2_p_tip.set_color(RED_E) + + pv3 = Line(start = ORIGIN,end = 4*UP+3*RIGHT+[0,0,5]) + pv3.set_color(GOLD_E) + pv3tip = Polygon(4*UP+3*RIGHT+[0,0,5],3.6*UP+2.7*RIGHT+[0,0,4.5]+0.1*UP+0.1*LEFT,3.6*UP+2.7*RIGHT+[0,0,4.5]+0.1*DOWN+0.1*RIGHT) + pv3tip.set_opacity(1) + pv3tip.set_fill(GOLD_E) + pv3tip.set_color(GOLD_E) + + v3_p = Line(start = ORIGIN,end = [0,0,5]) + v3_p.set_color(YELLOW_E) + v3_p_tip = Polygon([0,0,5],[0,0,4.8]+0.2*RIGHT,[0,0,4.8]+0.2*LEFT) + v3_p_tip.set_opacity(1) + v3_p_tip.set_fill(YELLOW_E) + v3_p_tip.set_color(YELLOW_E) + + self.stop_ambient_camera_rotation() + self.play(Transform(pv1,v1_p), Transform(pv1tip,v1_p_tip), Transform(pv2,v2_p), Transform(pv2tip,v2_p_tip), Transform(pv3,v3_p), Transform(pv3tip,v3_p_tip)) + self.play(FadeOut(dashedline1), + FadeOut(dashedline2), + FadeOut(dashedline3), + FadeOut(dashedline4), + FadeOut(dashedline5), + FadeOut(line1), + FadeOut(tip1), + FadeOut(line2), + FadeOut(tip2), + FadeOut(line3), + FadeOut(tip3), + FadeOut(text)) + + text = TextMobject(r"$v$ is the sum of projections on the orthonormal vectors") + text.set_color(GOLD_E) + text.scale(0.75) + self.add_fixed_in_frame_mobjects(text) + text.move_to(3*DOWN) + self.play(Write(text), ApplyMethod(pv2.move_to,(3.5*RIGHT + 3.5*UP+3*RIGHT+4*UP)/2), ApplyMethod(pv2tip.move_to,(3.1*RIGHT + 3.9*UP))) + self.play(ApplyMethod(pv3.move_to,3*RIGHT + 4*UP + [0,0,2.5]), ApplyMethod(pv3tip.move_to,(3*RIGHT + 4*UP + [0,0,4.8]))) + + self.wait(3)
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file4.gif b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file4.gif Binary files differnew file mode 100644 index 0000000..4891350 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file4.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file5.gif b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file5.gif Binary files differnew file mode 100644 index 0000000..47fc316 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file5.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file6.gif b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file6.gif Binary files differnew file mode 100644 index 0000000..d4ae50c --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/Orthonormal-Basis/file6.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/README.md b/FSF-2020/linear-algebra/linear-transformations/README.md index 692201e..cf81d01 100644 --- a/FSF-2020/linear-algebra/linear-transformations/README.md +++ b/FSF-2020/linear-algebra/linear-transformations/README.md @@ -1,9 +1,10 @@ # Contributer: Archit Sangal
My Github Account : <a href="https://github.com/architsangal">architsangal</a>
<br/></br>
+
## Sub-Topics Covered:
-+ Vector Space Homomorphisms (Linear Maps)
++ Linear Transformations (Linear Maps)
+ The Four Fundamental Subspaces
+ Rank-Nullity Theorem
+ Orthonormal basis
-+ Gramm-Schmidt Orthogonalization Process
++ Gramm-Schmidt Orthogonalization Process
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/README.md b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/README.md new file mode 100644 index 0000000..d21c4dc --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/README.md @@ -0,0 +1,30 @@ +# Contributer: Archit Sangal +My Github Account : <a href="https://github.com/architsangal">architsangal</a> +<br/></br> + +## Sub-Topics Covered: ++ The Four Fundamental Subspaces + +#### Video 1: Video 1: Writing System of linear equations in form of Ax=b + + +#### Video 2: Column Space is same as the image of Linear Transformation + + +#### Video 3: Existance of Solution w.r.t. vector b + + +#### Video 4: Null Space (Visually) + + +#### Video 5: Definition 1 is equivalent to Definition 2 + + +#### Video 6: Relation between Row Space and Null Space + + +#### Fig. 1 Naming of the left null space + + +#### Video 7: Left Null Space(Visually) +
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file10_Left_Null_Space_pSv8iio_d5Sy9qS.gif b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file10_Left_Null_Space_pSv8iio_d5Sy9qS.gif Binary files differnew file mode 100644 index 0000000..3f50635 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file10_Left_Null_Space_pSv8iio_d5Sy9qS.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file11.gif b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file11.gif Binary files differnew file mode 100644 index 0000000..8f74202 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file11.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file12.gif b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file12.gif Binary files differnew file mode 100644 index 0000000..aa7403b --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file12.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file13.gif b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file13.gif Binary files differnew file mode 100644 index 0000000..34b54c7 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file13.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file14.gif b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file14.gif Binary files differnew file mode 100644 index 0000000..b77791b --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file14.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file15.gif b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file15.gif Binary files differnew file mode 100644 index 0000000..8bb24bf --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file15.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file16.gif b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file16.gif Binary files differnew file mode 100644 index 0000000..87e0026 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file16.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file17.gif b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file17.gif Binary files differnew file mode 100644 index 0000000..eec819a --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file17.gif diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file1_Column_Space.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file18_NOT_in_lecture_note_Column_Space.py index afe4f9a..afe4f9a 100644 --- a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file1_Column_Space.py +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file18_NOT_in_lecture_note_Column_Space.py diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file1_Axb.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file1_Axb.py new file mode 100755 index 0000000..95d1021 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file1_Axb.py @@ -0,0 +1,77 @@ +from manimlib.imports import *
+
+class Axb(Scene):
+
+ def construct(self):
+
+ text0 = TextMobject("Linear System Of Equations")
+ text1 = TextMobject(r"$x_{1}+x_{2}+x_{3} =b_{1}$")
+ text2 = TextMobject(r"$x_{1}+2x_{2}+x_{3} =b_{2}$")
+ text3 = TextMobject(r"$x_{1}+x_{2}+3x_{3} =b_{3}$")
+ text0.move_to(UP*2+LEFT*2)
+ text0.set_color(DARK_BLUE)
+ text1.move_to(UP)
+ text2.move_to(ORIGIN)
+ text3.move_to(DOWN)
+
+ text0.scale(0.75)
+ text1.scale(0.75)
+ text2.scale(0.75)
+ text3.scale(0.75)
+ self.play(Write(text0))
+ self.play(Write(text1))
+ self.play(Write(text2))
+ self.play(Write(text3))
+ self.play(ApplyMethod(text0.move_to,3*UP+LEFT*2), ApplyMethod(text1.move_to,2.5*UP), ApplyMethod(text2.move_to,2*UP), ApplyMethod(text3.move_to,1.5*UP))
+
+ A = TextMobject(r"$\left( \begin{array}{c c c} 1 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 3 \end{array}\right) \left[ \begin{array} {c} x_{1} \\ x_{2} \\ x_{3} \end{array}\right] =$", r"$\left[ \begin{array}{c} x_{1}+x_{2}+x_{3} \\ x_{1}+2x_{2}+x_{3} \\ x_{1}+x_{2}+3x_{3} \end{array}\right]$")
+ A.scale(0.75)
+ self.play(FadeIn(A))
+
+ textA = TextMobject("A")
+ textx = TextMobject("x")
+ textb = TextMobject("Ax")
+
+ textA.move_to(DOWN+3*LEFT)
+ textx.move_to(1.1*DOWN+0.5*LEFT)
+ textb.move_to(DOWN-2*LEFT)
+
+ self.play(Write(textA), Write(textx), Write(textb))
+
+ circle1 = Circle(radius = 0.24)
+ circle2 = Circle(radius = 0.24)
+ square = Square(side_length = 0.6)
+
+ circle1.move_to(UP*0.5+LEFT*3.05)
+ circle2.move_to(UP*0.4+LEFT*0.5)
+ square.move_to(UP*0.4+RIGHT*1.3)
+
+ self.play(FadeIn(circle1), FadeIn(circle2),FadeIn(square))
+
+ self.play(ApplyMethod(circle1.move_to,UP*0.5+LEFT*2.45), ApplyMethod(circle2.move_to,LEFT*0.5), ApplyMethod(square.move_to,UP*0.4+RIGHT*2.2))
+ self.play(ApplyMethod(circle1.move_to,UP*0.5+LEFT*1.85), ApplyMethod(circle2.move_to,DOWN*0.5+LEFT*0.5), ApplyMethod(square.move_to,UP*0.4+RIGHT*3.1))
+
+ self.play(ApplyMethod(circle1.move_to,LEFT*3.05), ApplyMethod(circle2.move_to,UP*0.4+LEFT*0.5), ApplyMethod(square.move_to,RIGHT*1.3))
+ self.play(ApplyMethod(circle1.move_to,LEFT*2.45), ApplyMethod(circle2.move_to,LEFT*0.5), ApplyMethod(square.move_to,RIGHT*2.2))
+ self.play(ApplyMethod(circle1.move_to,LEFT*1.85), ApplyMethod(circle2.move_to,DOWN*0.5+LEFT*0.5), ApplyMethod(square.move_to,RIGHT*3.1))
+
+ self.play(ApplyMethod(circle1.move_to,0.4*DOWN+LEFT*3.05), ApplyMethod(circle2.move_to,UP*0.4+LEFT*0.5), ApplyMethod(square.move_to,0.4*DOWN+RIGHT*1.3))
+ self.play(ApplyMethod(circle1.move_to,0.4*DOWN+LEFT*2.45), ApplyMethod(circle2.move_to,LEFT*0.5), ApplyMethod(square.move_to,0.4*DOWN+RIGHT*2.2))
+ self.play(ApplyMethod(circle1.move_to,0.4*DOWN+LEFT*1.85), ApplyMethod(circle2.move_to,DOWN*0.5+LEFT*0.5), ApplyMethod(square.move_to,0.4*DOWN+RIGHT*3.1))
+
+ self.play(FadeOut(circle1), FadeOut(circle2), FadeOut(square))
+ self.play(FadeOut(A[0]), ApplyMethod(A[1].move_to,2*LEFT),ApplyMethod(textb.move_to,DOWN+1.7*LEFT), FadeOut(textx), FadeOut(textA))
+ b = TextMobject(r"$=\left[ \begin{array}{c} b_{1} \\ b_{2} \\ b_{3} \end{array}\right]$")
+ b.move_to(RIGHT)
+ textB = TextMobject("b")
+ textB.move_to(1.2*DOWN+1.1*RIGHT)
+ self.play(FadeIn(b),FadeIn(textB))
+
+ self.wait()
+
+ self.play(FadeOut(text0), FadeOut(text1), FadeOut(text2), FadeOut(text3))
+
+ axb = TextMobject("Ax = b")
+ self.play(FadeIn(axb), FadeOut(textb), FadeOut(textB), FadeOut(b), FadeOut(A[1]))
+
+ self.wait()
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file1_Column_Space.gif b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file1_Column_Space.gif Binary files differdeleted file mode 100644 index 7d8d2e1..0000000 --- a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file1_Column_Space.gif +++ /dev/null diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file2_CSasImage.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file2_CSasImage.py new file mode 100644 index 0000000..70547cb --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file2_CSasImage.py @@ -0,0 +1,169 @@ +from manimlib.imports import * + +class Column_Space(Scene): + def construct(self): + + A = TextMobject(r"$A = $",r"$\left( \begin{array}{c c} 1 & 2 \\ 3 & 4 \end{array} \right)$") + A.move_to(2*UP) + A[1].set_color(color = DARK_BLUE) + A.scale(0.75) + + self.play(Write(A),run_time = 1) + + CS_A = TextMobject(r"Column Space of $A = x_{1}$",r"$\left( \begin{array}{c} 1 \\ 3 \end{array} \right)$",r"$+x_{2}$",r"$ \left( \begin{array}{c} 2 \\ 4\end{array} \right)$") + CS_A.move_to(1.5*LEFT+1*DOWN) + CS_A[1].set_color(color = DARK_BLUE) + CS_A[3].set_color(color = DARK_BLUE) + CS_A.scale(0.75) + + self.play(Write(CS_A),run_time = 2) + + arrow1 = Arrow(start = 1.25*UP,end = (0.25*DOWN+1.75*LEFT+0.25*DOWN+1.2*RIGHT)/2) + arrow3 = Arrow(start = 1.25*UP+0.75*RIGHT,end = (0.25*DOWN+2.9*RIGHT+0.25*DOWN)/2) + + arrow1.scale(1.5) + arrow3.scale(1.5) + + Defn = TextMobject("Linear Combination of Columns of Matrix") + Defn.move_to(3*DOWN) + + self.play(Write(Defn), ShowCreation(arrow1), ShowCreation(arrow3),run_time = 1) + self.wait(1) + +class solution(LinearTransformationScene): + def construct(self): + + self.setup() + self.wait() + + o = TextMobject(r"Consider the vector space $R^2$") + o.move_to(2*DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait() + self.play(FadeOut(o)) + + A = TextMobject(r"Let $A$ be ",r"$\left[\begin{array}{c c} 1 & -1 \\ 1 & -1 \end{array}\right]$",r". $A$ denotes the matrix the of this linear transformation.") + A.move_to(2*DOWN) + A.scale(0.75) + A.add_background_rectangle() + self.play(Write(A)) + matrix = [[1,-1],[1,-1]] + self.apply_matrix(matrix) + self.wait() + self.play(FadeOut(A)) + + o = TextMobject(r"This is the transformed vector space") + o.move_to(2*DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait() + self.play(FadeOut(o)) + + texti = TextMobject(r"$\left[\begin{array}{c}1\\1\end{array}\right]$") + textj = TextMobject(r"$\left[\begin{array}{c}-1\\-1\end{array}\right]$") + texti.set_color(GREEN) + textj.set_color(RED) + texti.scale(0.7) + textj.scale(0.7) + texti.move_to(1.35*RIGHT+0.5*UP) + textj.move_to(-(1.5*RIGHT+0.5*UP)) + + text1 = TextMobject("[") + text2 = TextMobject(r"$\begin{array}{c} 1 \\ 1 \end{array}$") + text3 = TextMobject(r"$\begin{array}{c} -1 \\ -1 \end{array}$") + text4 = TextMobject("]") + + text2.set_color(GREEN) + text3.set_color(RED) + + text1.scale(2) + text4.scale(2) + text2.scale(0.7) + text3.scale(0.7) + + text1.move_to(2.5*UP+6*LEFT) + text2.move_to(2.5*UP+5.75*LEFT) + text3.move_to(2.5*UP+5.25*LEFT) + text4.move_to(2.5*UP+5*LEFT) + + self.play(Write(texti), Write(textj)) + self.wait() + self.play(FadeIn(text1), Transform(texti,text2), Transform(textj,text3), FadeIn(text4)) + self.wait() + + o = TextMobject(r"Now, you can observe the Image of Linear Transformation") + o1 = TextMobject(r"and Column Space(i.e. span of columns of matrix $A$) are same") + o.move_to(2.5*DOWN) + o1.move_to(3*DOWN) + o.scale(0.75) + o1.scale(0.75) + o.add_background_rectangle() + o1.add_background_rectangle() + self.play(Write(o)) + self.play(Write(o1)) + self.wait() + self.play(FadeOut(o),FadeOut(o1)) + +class solution2nd(LinearTransformationScene): + def construct(self): + + self.setup() + self.wait() + + arrow1 = Arrow(start = ORIGIN,end = 2*DOWN+RIGHT) + arrow2 = Arrow(start = ORIGIN,end = UP+LEFT) + arrow3 = Arrow(start = ORIGIN,end = 3*UP+4*RIGHT) + arrow1.set_color(YELLOW) + arrow2.set_color(ORANGE) + arrow3.set_color(PURPLE) + arrow1.scale(1.3) + arrow2.scale(1.5) + arrow3.scale(1.1) + + self.play(ShowCreation(arrow1), ShowCreation(arrow2), ShowCreation(arrow3)) + + self.add_transformable_mobject(arrow1) + self.add_transformable_mobject(arrow2) + self.add_transformable_mobject(arrow3) + o = TextMobject(r"Consider any vector in the original vector space $R^2$") + o.move_to(2.5*DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait() + self.play(FadeOut(o)) + + A = TextMobject(r"Let the matrix the of this linear transformation be $A$ =",r"$\left[\begin{array}{c c} 1 & -1 \\ 1 & -1 \end{array}\right]$",r" again.") + A.move_to(2*DOWN) + A.scale(0.75) + A.add_background_rectangle() + self.play(Write(A)) + matrix = [[1,-1],[1,-1]] + self.apply_matrix(matrix) + self.wait() + self.play(FadeOut(A)) + + o = TextMobject(r"This is the transformed vector space") + o.move_to(2*DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait() + self.play(FadeOut(o)) + + o = TextMobject(r"Each and every vector of original vector space $R^2$ will transform") + o1 = TextMobject(r"to this new vector space which is spanned by $\mathbf{CS}(A)$") + o.move_to(2.5*DOWN) + o1.move_to(3*DOWN) + o.scale(0.75) + o1.scale(0.75) + o.add_background_rectangle() + o1.add_background_rectangle() + self.play(Write(o)) + self.play(Write(o1)) + self.wait() + self.play(FadeOut(o)) + self.play(FadeOut(o1))
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file3_solution.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file3_solution.py new file mode 100644 index 0000000..eb310f3 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file3_solution.py @@ -0,0 +1,77 @@ +from manimlib.imports import * +class solution(LinearTransformationScene): + def construct(self): + + self.setup() + self.wait() + + o = TextMobject(r"This is the original vector space $R^2$ (before Linear Transformation)") + o.move_to(3*DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait() + self.play(FadeOut(o)) + + A = TextMobject(r"Consider the matrix the of this linear transformation $A$ = $\left[\begin{array}{c c} 1 & -1 \\ 1 & -1 \end{array}\right]$") + A.move_to(3*DOWN) + A.scale(0.75) + A.add_background_rectangle() + self.play(Write(A)) + matrix = [[1,-1],[1,-1]] + self.apply_matrix(matrix) + self.wait() + self.play(FadeOut(A)) + + o = TextMobject(r"This is the transformed vector space") + o.move_to(3*DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait() + self.play(FadeOut(o)) + + arrow2 = Arrow(start = ORIGIN, end = 2*DOWN+2*LEFT) + arrow2.set_color(PURPLE) + arrow2.scale(1.2) + self.play(ShowCreation(arrow2)) + self.wait() + + o1 = TextMobject("If the ","vector b"," lies in the transformed vector space") + o2 = TextMobject("(the line) then the solution exist") + o1.move_to(2.5*DOWN+2*RIGHT) + o1[1].set_color(PURPLE) + o2.move_to(3*DOWN+2.5*RIGHT) + o1.scale(0.75) + o2.scale(0.75) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + self.wait() + self.play(FadeOut(o1), FadeOut(o2)) + + self.play(FadeOut(arrow2)) + + arrow1 = Arrow(start = ORIGIN, end = 2*UP+RIGHT) + arrow1.set_color(ORANGE) + arrow1.scale(1.3) + self.play(ShowCreation(arrow1)) + self.wait() + + o1 = TextMobject("If the ","vector b"," does lies in the transformed") + o2 = TextMobject("vector space then the does not solution exist") + o1.move_to(2.5*DOWN+2*RIGHT) + o1[1].set_color(ORANGE) + o2.move_to(3*DOWN+2.5*RIGHT) + o1.scale(0.75) + o2.scale(0.75) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + self.wait() + self.play(FadeOut(o1), FadeOut(o2)) + + self.play(FadeOut(arrow1)) +
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file4_null_space.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file4_null_space.py new file mode 100644 index 0000000..3c52677 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file4_null_space.py @@ -0,0 +1,91 @@ +from manimlib.imports import * +class null_space(LinearTransformationScene): + def construct(self): + + self.setup() + self.wait() + + o = TextMobject(r"This is the original vector space $R^2$(before Linear Transformation)") + o.move_to(3*DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait() + self.play(FadeOut(o)) + + o1 = TextMobject("Consider a set of vectors which are linear") + o2 = TextMobject(r"span of a particular vector $\left(\begin{array}{c} 1 \\ 1 \end{array}\right)$") + o1.move_to(2*DOWN+3*RIGHT) + o2.move_to(2.75*DOWN+3*RIGHT) + o1.scale(0.7) + o2.scale(0.7) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + + arrow = Arrow(start = ORIGIN, end = UP+RIGHT) + arrow1 = Arrow(start = ORIGIN, end = 2*(UP+RIGHT)) + arrow2 = Arrow(start = ORIGIN, end = 3*(UP+RIGHT)) + arrow3 = Arrow(start = ORIGIN, end = 4*(UP+RIGHT)) + arrow4 = Arrow(start = ORIGIN, end = DOWN+LEFT) + arrow5 = Arrow(start = ORIGIN, end = 2*(DOWN+LEFT)) + arrow6 = Arrow(start = ORIGIN, end = 3*(DOWN+LEFT)) + arrow7 = Arrow(start = ORIGIN, end = 4*(DOWN+LEFT)) + + arrow.scale(1.5) + arrow1.scale(1.2) + arrow2.scale(1.15) + arrow3.scale(1.1) + arrow4.scale(1.5) + arrow5.scale(1.2) + arrow6.scale(1.15) + arrow7.scale(1.1) + + self.play(ShowCreation(arrow), + ShowCreation(arrow1), + ShowCreation(arrow2), + ShowCreation(arrow3), + ShowCreation(arrow4), + ShowCreation(arrow5), + ShowCreation(arrow6), + ShowCreation(arrow7), + ) + + self.wait(2) + self.play(FadeOut(o1), FadeOut(o2)) + + self.add_transformable_mobject(arrow) + self.add_transformable_mobject(arrow1) + self.add_transformable_mobject(arrow2) + self.add_transformable_mobject(arrow3) + self.add_transformable_mobject(arrow4) + self.add_transformable_mobject(arrow5) + self.add_transformable_mobject(arrow6) + self.add_transformable_mobject(arrow7) + + o1 = TextMobject("Notice, entire set of vectors which belongs to the vector") + o2 = TextMobject(r"subspace(Linear Span of $\left(\begin{array}{c} 1 \\ 1 \end{array}\right)$) transforms to zero") + o1.move_to(2*DOWN+2.5*RIGHT) + o2.move_to(2.75*DOWN+2.5*RIGHT) + o1.scale(0.7) + o2.scale(0.7) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + self.wait() + + matrix = [[1,-1],[1,-1]] + self.apply_matrix(matrix) + self.wait() + + self.play(FadeOut(o1), FadeOut(o2)) + + o = TextMobject(r"Hence, the vector space formed by linear span of $\left(\begin{array}{c} 1 \\ 1 \end{array}\right)$ is the null space of $A$") + o.move_to(3*DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait(2) + self.play(FadeOut(o), FadeOut(arrow), FadeOut(arrow1), FadeOut(arrow2), FadeOut(arrow3), FadeOut(arrow4), FadeOut(arrow5), FadeOut(arrow6), FadeOut(arrow7)) diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file5_Row_Space_part_1.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file5_Row_Space_part_1.py new file mode 100644 index 0000000..5259eb4 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file5_Row_Space_part_1.py @@ -0,0 +1,68 @@ +from manimlib.imports import * +class LS(Scene): + def construct(self): + text1 = TextMobject(r"Consider a matrix $A =$") + text2 = TextMobject(r"[") + text3 = TextMobject(r"$\begin{array}{c c} 1 & -2\end{array}$") + text4 = TextMobject(r"$\begin{array}{c c} 1 & -1\end{array}$") + text5 = TextMobject(r"]") + + text2.scale(2) + text5.scale(2) + + text1.set_color(DARK_BLUE) + text2.set_color(DARK_BLUE) + text3.set_color(PURPLE) + text4.set_color(YELLOW) + text5.set_color(DARK_BLUE) + + text1.move_to(3.5*LEFT+3*UP+2*RIGHT) + text2.move_to(0.75*LEFT+3*UP+2*RIGHT) + text3.move_to(3.25*UP+2*RIGHT) + text4.move_to(2.75*UP+2*RIGHT) + text5.move_to(0.75*RIGHT+3*UP+2*RIGHT) + + self.play(FadeIn(text1), FadeIn(text2), FadeIn(text3), FadeIn(text4), FadeIn(text5)) + self.wait() + + ttext1 = TextMobject(r"$A^T =$") + ttext2 = TextMobject(r"[") + ttext3 = TextMobject(r"$\begin{array}{c} 1 \\ -2\end{array}$") + ttext4 = TextMobject(r"$\begin{array}{c} 1 \\ -1\end{array}$") + ttext5 = TextMobject(r"]") + + ttext2.scale(2) + ttext5.scale(2) + + ttext1.set_color(DARK_BLUE) + ttext2.set_color(DARK_BLUE) + ttext3.set_color(PURPLE) + ttext4.set_color(YELLOW) + ttext5.set_color(DARK_BLUE) + + ttext1.move_to(2*LEFT+1.5*UP+2*RIGHT) + ttext2.move_to(1*LEFT+1.5*UP+2*RIGHT) + ttext3.move_to(0.5*LEFT+1.5*UP+2*RIGHT) + ttext4.move_to(0.5*RIGHT+1.5*UP+2*RIGHT) + ttext5.move_to(1*RIGHT+1.5*UP+2*RIGHT) + + self.play(FadeIn(ttext1), FadeIn(ttext2), FadeIn(ttext3), FadeIn(ttext4), FadeIn(ttext5)) + + rtext = TextMobject(r"Row Space of $A$ = Column Space of $A^T = a_1$",r"$\left[\begin{array}{c} 1 \\ -2\end{array}\right]$",r"$+a_2$",r"$\left[\begin{array}{c} 1 \\ -1\end{array}\right]$") + rtext[1].set_color(PURPLE) + rtext[3].set_color(YELLOW) + rtext.move_to(2*DOWN+1.5*LEFT) + rtext.scale(0.75) + + self.play(Write(rtext)) + self.wait() + + arrow1 = Arrow(start = 1.5*RIGHT+UP, end = 1.25*(DOWN+RIGHT)) + arrow2 = Arrow(start = 2.5*RIGHT+UP, end = 1.25*DOWN+3.25*RIGHT) + arrow1.scale(1.25) + arrow2.scale(1.25) + arrow1.set_color(PURPLE) + arrow2.set_color(YELLOW) + + self.play(ShowCreation(arrow1), ShowCreation(arrow2)) + self.wait(2) diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file2_Row_Space.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file6_Row_Space_part_2.py index b16a32a..b16a32a 100644 --- a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file2_Row_Space.py +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file6_Row_Space_part_2.py diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file7_Row_space_Orthogonal_Complements.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file7_Row_space_Orthogonal_Complements.py new file mode 100644 index 0000000..c81d370 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file7_Row_space_Orthogonal_Complements.py @@ -0,0 +1,150 @@ +from manimlib.imports import * +class row_space(LinearTransformationScene): + def construct(self): + + self.setup() + self.wait() + + o = TextMobject(r"This is the original vector space $R^2$(before Linear Transformation)") + o.move_to(DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait() + self.play(FadeOut(o)) + + o1 = TextMobject("Consider a set of vectors which are linear") + o2 = TextMobject(r"span of a $\left(\begin{array}{c} 1 \\ 1 \end{array}\right)$i.e. the null space.") + o1.move_to(2*DOWN+3*RIGHT) + o2.move_to(2.75*DOWN+3*RIGHT) + o1.scale(0.7) + o2.scale(0.7) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + + arrow = Arrow(start = ORIGIN, end = UP+RIGHT) + arrow.set_color(YELLOW) + arrow1 = Arrow(start = ORIGIN, end = 2*(UP+RIGHT)) + arrow1.set_color(YELLOW) + arrow2 = Arrow(start = ORIGIN, end = 3*(UP+RIGHT)) + arrow2.set_color(YELLOW) + arrow3 = Arrow(start = ORIGIN, end = 4*(UP+RIGHT)) + arrow3.set_color(YELLOW) + arrow4 = Arrow(start = ORIGIN, end = DOWN+LEFT) + arrow4.set_color(YELLOW) + arrow5 = Arrow(start = ORIGIN, end = 2*(DOWN+LEFT)) + arrow5.set_color(YELLOW) + arrow6 = Arrow(start = ORIGIN, end = 3*(DOWN+LEFT)) + arrow6.set_color(YELLOW) + arrow7 = Arrow(start = ORIGIN, end = 4*(DOWN+LEFT)) + arrow7.set_color(YELLOW) + + arrow.scale(1.5) + arrow1.scale(1.2) + arrow2.scale(1.15) + arrow3.scale(1.1) + arrow4.scale(1.5) + arrow5.scale(1.2) + arrow6.scale(1.15) + arrow7.scale(1.1) + + self.play(ShowCreation(arrow), + ShowCreation(arrow1), + ShowCreation(arrow2), + ShowCreation(arrow3), + ShowCreation(arrow4), + ShowCreation(arrow5), + ShowCreation(arrow6), + ShowCreation(arrow7), + ) + + self.wait(2) + self.play(FadeOut(o1), FadeOut(o2)) + + o1 = TextMobject("Consider a set of vectors which are linear") + o2 = TextMobject(r"span of a $\left(\begin{array}{c} 1 \\ -1 \end{array}\right)$i.e. the row space.") + o1.move_to(2*DOWN+3*RIGHT) + o2.move_to(2.75*DOWN+3*RIGHT) + o1.scale(0.7) + o2.scale(0.7) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + + rarrow = Arrow(start = ORIGIN, end = -UP+RIGHT) + rarrow.set_color(PURPLE) + rarrow1 = Arrow(start = ORIGIN, end = 2*(-UP+RIGHT)) + rarrow1.set_color(PURPLE) + rarrow2 = Arrow(start = ORIGIN, end = 3*(-UP+RIGHT)) + rarrow2.set_color(PURPLE) + rarrow3 = Arrow(start = ORIGIN, end = 4*(-UP+RIGHT)) + rarrow3.set_color(PURPLE) + rarrow4 = Arrow(start = ORIGIN, end = -DOWN+LEFT) + rarrow4.set_color(PURPLE) + rarrow5 = Arrow(start = ORIGIN, end = 2*(-DOWN+LEFT)) + rarrow5.set_color(PURPLE) + rarrow6 = Arrow(start = ORIGIN, end = 3*(-DOWN+LEFT)) + rarrow6.set_color(PURPLE) + rarrow7 = Arrow(start = ORIGIN, end = 4*(-DOWN+LEFT)) + rarrow7.set_color(PURPLE) + + rarrow.scale(1.5) + rarrow1.scale(1.2) + rarrow2.scale(1.15) + rarrow3.scale(1.1) + rarrow4.scale(1.5) + rarrow5.scale(1.2) + rarrow6.scale(1.15) + rarrow7.scale(1.1) + + self.play(ShowCreation(rarrow), + ShowCreation(rarrow1), + ShowCreation(rarrow2), + ShowCreation(rarrow3), + ShowCreation(rarrow4), + ShowCreation(rarrow5), + ShowCreation(rarrow6), + ShowCreation(rarrow7), + ) + + self.wait(2) + self.play(FadeOut(o1), FadeOut(o2)) + + self.add_transformable_mobject(arrow) + self.add_transformable_mobject(arrow1) + self.add_transformable_mobject(arrow2) + self.add_transformable_mobject(arrow3) + self.add_transformable_mobject(arrow4) + self.add_transformable_mobject(arrow5) + self.add_transformable_mobject(arrow6) + self.add_transformable_mobject(arrow7) + + self.add_transformable_mobject(rarrow) + self.add_transformable_mobject(rarrow1) + self.add_transformable_mobject(rarrow2) + self.add_transformable_mobject(rarrow3) + self.add_transformable_mobject(rarrow4) + self.add_transformable_mobject(rarrow5) + self.add_transformable_mobject(rarrow6) + self.add_transformable_mobject(rarrow7) + + o1 = TextMobject("Notice, entire set of vectors which belong to the null space of $A$ transforms to zero") + o2 = TextMobject(r"and entire set of vectors which belong to the row space of $A$ transforms to column space of $A$.") + o1.move_to(2.5*DOWN) + o2.move_to(3.5*DOWN) + o1.scale(0.7) + o2.scale(0.7) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + self.wait() + + matrix = [[1,-1],[1,-1]] + self.apply_matrix(matrix) + self.wait(3) + + self.play(FadeOut(o1), FadeOut(o2))
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file8_Left_Null_Space.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file8_Left_Null_Space.py new file mode 100755 index 0000000..fd05e75 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file8_Left_Null_Space.py @@ -0,0 +1,26 @@ +from manimlib.imports import * + +class Left_Null_Space(Scene): + def construct(self): + + A = TextMobject(r"Left Null Space of A") + A.move_to(3*UP) + defn = TextMobject(r"It is a vector space that consists of all the solution $x$ to the equation $A^{T}x=0$") + defn.move_to(2*UP) + defn.scale(0.75) + eqn1 = TextMobject(r"$A^{T}x=0 \cdots (i)$") + eqn1.move_to(UP) + self.play(Write(A), Write(defn), Write(eqn1),run_time=1) + statement = TextMobject(r"Taking transpose of eqn $(i)$") + eqn = TextMobject(r"$(A^{T}x)^{T}=0$") + eqn.move_to(DOWN) + eqn2 = TextMobject(r"$x^{T}(A^{T})^{T}=0$") + eqn2.move_to(DOWN) + eqn3 = TextMobject(r"$x^{T}A=0$") + eqn3.move_to(DOWN) + self.play(Write(statement),Write(eqn),run_time=1) + self.wait(0.5) + self.play(Transform(eqn,eqn2),run_time=1) + self.wait(0.5) + self.play(Transform(eqn,eqn3),run_time=1) + self.wait(0.5)
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file9_left_null_space.py b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file9_left_null_space.py new file mode 100644 index 0000000..61285be --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Four-Fundamental-Subspaces/file9_left_null_space.py @@ -0,0 +1,186 @@ +from manimlib.imports import * +class row_space(LinearTransformationScene): + def construct(self): + + self.setup() + self.wait() + + o = TextMobject(r"This is the original vector space $R^2$(before Linear Transformation)") + o.move_to(DOWN) + o.scale(0.75) + o.add_background_rectangle() + self.play(Write(o)) + self.wait() + self.play(FadeOut(o)) + + o1 = TextMobject("Consider a set of vectors which are linear") + o2 = TextMobject(r"span of a $\left(\begin{array}{c} 1 \\ 1 \end{array}\right)$i.e. the null space.") + o1.move_to(2*DOWN+3*RIGHT) + o2.move_to(2.75*DOWN+3*RIGHT) + o1.scale(0.7) + o2.scale(0.7) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + + arrow = Arrow(start = ORIGIN, end = UP+RIGHT) + arrow.set_color(YELLOW) + arrow1 = Arrow(start = ORIGIN, end = 2*(UP+RIGHT)) + arrow1.set_color(YELLOW) + arrow2 = Arrow(start = ORIGIN, end = 3*(UP+RIGHT)) + arrow2.set_color(YELLOW) + arrow3 = Arrow(start = ORIGIN, end = 4*(UP+RIGHT)) + arrow3.set_color(YELLOW) + arrow4 = Arrow(start = ORIGIN, end = DOWN+LEFT) + arrow4.set_color(YELLOW) + arrow5 = Arrow(start = ORIGIN, end = 2*(DOWN+LEFT)) + arrow5.set_color(YELLOW) + arrow6 = Arrow(start = ORIGIN, end = 3*(DOWN+LEFT)) + arrow6.set_color(YELLOW) + arrow7 = Arrow(start = ORIGIN, end = 4*(DOWN+LEFT)) + arrow7.set_color(YELLOW) + + arrow.scale(1.5) + arrow1.scale(1.2) + arrow2.scale(1.15) + arrow3.scale(1.1) + arrow4.scale(1.5) + arrow5.scale(1.2) + arrow6.scale(1.15) + arrow7.scale(1.1) + + self.play(ShowCreation(arrow), + ShowCreation(arrow1), + ShowCreation(arrow2), + ShowCreation(arrow3), + ShowCreation(arrow4), + ShowCreation(arrow5), + ShowCreation(arrow6), + ShowCreation(arrow7), + ) + + self.wait(2) + self.play(FadeOut(o1), FadeOut(o2)) + + o1 = TextMobject("Consider a set of vectors which are linear") + o2 = TextMobject(r"span of a vector $\left(\begin{array}{c} 1 \\ -1 \end{array}\right)$i.e. the row space.") + o1.move_to(2*DOWN+3*RIGHT) + o2.move_to(2.75*DOWN+3*RIGHT) + o1.scale(0.7) + o2.scale(0.7) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + + rarrow = Arrow(start = ORIGIN, end = -UP+RIGHT) + rarrow.set_color(PURPLE) + rarrow1 = Arrow(start = ORIGIN, end = 2*(-UP+RIGHT)) + rarrow1.set_color(PURPLE) + rarrow2 = Arrow(start = ORIGIN, end = 3*(-UP+RIGHT)) + rarrow2.set_color(PURPLE) + rarrow3 = Arrow(start = ORIGIN, end = 4*(-UP+RIGHT)) + rarrow3.set_color(PURPLE) + rarrow4 = Arrow(start = ORIGIN, end = -DOWN+LEFT) + rarrow4.set_color(PURPLE) + rarrow5 = Arrow(start = ORIGIN, end = 2*(-DOWN+LEFT)) + rarrow5.set_color(PURPLE) + rarrow6 = Arrow(start = ORIGIN, end = 3*(-DOWN+LEFT)) + rarrow6.set_color(PURPLE) + rarrow7 = Arrow(start = ORIGIN, end = 4*(-DOWN+LEFT)) + rarrow7.set_color(PURPLE) + + rarrow.scale(1.5) + rarrow1.scale(1.2) + rarrow2.scale(1.15) + rarrow3.scale(1.1) + rarrow4.scale(1.5) + rarrow5.scale(1.2) + rarrow6.scale(1.15) + rarrow7.scale(1.1) + + self.play(ShowCreation(rarrow), + ShowCreation(rarrow1), + ShowCreation(rarrow2), + ShowCreation(rarrow3), + ShowCreation(rarrow4), + ShowCreation(rarrow5), + ShowCreation(rarrow6), + ShowCreation(rarrow7), + ) + + self.wait(2) + self.play(FadeOut(o1), FadeOut(o2)) + + self.add_transformable_mobject(arrow) + self.add_transformable_mobject(arrow1) + self.add_transformable_mobject(arrow2) + self.add_transformable_mobject(arrow3) + self.add_transformable_mobject(arrow4) + self.add_transformable_mobject(arrow5) + self.add_transformable_mobject(arrow6) + self.add_transformable_mobject(arrow7) + + self.add_transformable_mobject(rarrow) + self.add_transformable_mobject(rarrow1) + self.add_transformable_mobject(rarrow2) + self.add_transformable_mobject(rarrow3) + self.add_transformable_mobject(rarrow4) + self.add_transformable_mobject(rarrow5) + self.add_transformable_mobject(rarrow6) + self.add_transformable_mobject(rarrow7) + + matrix = [[1,-1],[1,-1]] + self.apply_matrix(matrix) + self.wait(3) + + o1 = TextMobject("Consider a set of vectors which are linear span of a vector") + o2 = TextMobject(r"$\left(\begin{array}{c} 1 \\ -1 \end{array}\right)$ which is orthogonal to column space i.e. Left Null Space") + o1.move_to(2*DOWN) + o2.move_to(2.75*DOWN) + o1.scale(0.7) + o2.scale(0.7) + o1.add_background_rectangle() + o2.add_background_rectangle() + self.play(Write(o1)) + self.play(Write(o2)) + + rarrow = Arrow(start = ORIGIN, end = -UP+RIGHT) + rarrow.set_color(YELLOW) + rarrow1 = Arrow(start = ORIGIN, end = 2*(-UP+RIGHT)) + rarrow1.set_color(YELLOW) + rarrow2 = Arrow(start = ORIGIN, end = 3*(-UP+RIGHT)) + rarrow2.set_color(YELLOW) + rarrow3 = Arrow(start = ORIGIN, end = 4*(-UP+RIGHT)) + rarrow3.set_color(YELLOW) + rarrow4 = Arrow(start = ORIGIN, end = -DOWN+LEFT) + rarrow4.set_color(YELLOW) + rarrow5 = Arrow(start = ORIGIN, end = 2*(-DOWN+LEFT)) + rarrow5.set_color(YELLOW) + rarrow6 = Arrow(start = ORIGIN, end = 3*(-DOWN+LEFT)) + rarrow6.set_color(YELLOW) + rarrow7 = Arrow(start = ORIGIN, end = 4*(-DOWN+LEFT)) + rarrow7.set_color(YELLOW) + + rarrow.scale(1.5) + rarrow1.scale(1.2) + rarrow2.scale(1.15) + rarrow3.scale(1.1) + rarrow4.scale(1.5) + rarrow5.scale(1.2) + rarrow6.scale(1.15) + rarrow7.scale(1.1) + + self.play(ShowCreation(rarrow), + ShowCreation(rarrow1), + ShowCreation(rarrow2), + ShowCreation(rarrow3), + ShowCreation(rarrow4), + ShowCreation(rarrow5), + ShowCreation(rarrow6), + ShowCreation(rarrow7), + ) + + self.wait(2) + self.play(FadeOut(o1), FadeOut(o2)) diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Rank-Nullity-Theorem/README.md b/FSF-2020/linear-algebra/linear-transformations/The-Rank-Nullity-Theorem/README.md new file mode 100644 index 0000000..ee1a337 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Rank-Nullity-Theorem/README.md @@ -0,0 +1,9 @@ +# Contributer: Archit Sangal +My Github Account : <a href="https://github.com/architsangal">architsangal</a> +<br/></br> + +## Sub-Topics Covered: ++ The Rank-Nullity Theorem + +#### Video 1: Visually understanding linear transformation(using grid) +
\ No newline at end of file diff --git a/FSF-2020/linear-algebra/linear-transformations/The-Rank-Nullity-Theorem/file2.gif b/FSF-2020/linear-algebra/linear-transformations/The-Rank-Nullity-Theorem/file2.gif Binary files differnew file mode 100644 index 0000000..46efc66 --- /dev/null +++ b/FSF-2020/linear-algebra/linear-transformations/The-Rank-Nullity-Theorem/file2.gif |
