<< Symphony Toolbox Symphony Toolbox qpipopt_mat >>
Symphony Toolbox >> Symphony Toolbox > qpipopt

qpipopt

Solves a linear quadratic problem.

Calling Sequence

xopt = qpipopt(nbVar,nbCon,Q,p,LB,UB,conMatrix,conLB,conUB)
[xopt,fopt,exitflag,output,lamda] = qpipopt( ... )

Parameters

nbVar :

a 1 x 1 matrix of doubles, number of variables

nbCon :

a 1 x 1 matrix of doubles, number of constraints

Q :

a n x n symmetric matrix of doubles, where n is number of variables, represents coefficients of quadratic in the quadratic problem.

p :

a 1 x n matrix of doubles, where n is number of variables, represents coefficients of linear in the quadratic problem

LB :

a 1 x n matrix of doubles, where n is number of variables, contains lower bounds of the variables.

UB :

a 1 x n matrix of doubles, where n is number of variables, contains upper bounds of the variables.

conMatrix :

a m x n matrix of doubles, where n is number of variables and m is number of constraints, contains matrix representing the constraint matrix

conLB :

a m x 1 matrix of doubles, where m is number of constraints, contains lower bounds of the constraints.

conUB :

a m x 1 matrix of doubles, where m is number of constraints, contains upper bounds of the constraints.

xopt :

a 1xn matrix of doubles, the computed solution of the optimization problem.

fopt :

a 1x1 matrix of doubles, the function value at x.

exitflag :

Integer identifying the reason the algorithm terminated.

output :

Structure containing information about the optimization.

lambda :

Structure containing the Lagrange multipliers at the solution x (separated by constraint type).

Description

Search the minimum of a constrained linear quadratic optimization problem specified by : find the minimum of f(x) such that

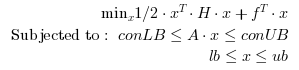
We are calling IPOpt for solving the quadratic problem, IPOpt is a library written in C++. The code has been written by ​Andreas Wächter and ​Carl Laird.

Examples

//Find x in R^6 such that:
conMatrix= [1,-1,1,0,3,1;
-1,0,-3,-4,5,6;
2,5,3,0,1,0
0,1,0,1,2,-1;
-1,0,2,1,1,0];
conLB=[1;2;3;-%inf;-%inf];
conUB = [1;2;3;-1;2.5];
lb=[-1000;-10000; 0; -1000; -1000; -1000];
ub=[10000; 100; 1.5; 100; 100; 1000];
//and minimize 0.5*x'*Q*x + p'*x with
p=[1; 2; 3; 4; 5; 6]; Q=eye(6,6);
nbVar = 6;
nbCon = 5;
[xopt,fopt,exitflag,output,lambda]=qpipopt(nbVar,nbCon,Q,p,lb,ub,conMatrix,conLB,conUB)

Examples

//Find the value of x that minimize following function
// f(x) = 0.5*x1^2 + x2^2 - x1*x2 - 2*x1 - 6*x2
// Subject to:
// x1 + x2 ≤ 2
// –x1 + 2x2 ≤ 2
// 2x1 + x2 ≤ 3
// 0 ≤ x1, 0 ≤ x2.
Q = [1 -1; -1 2];
p = [-2; -6];
conMatrix = [1 1; -1 2; 2 1];
conUB = [2; 2; 3];
conLB = [-%inf; -%inf; -%inf];
lb = [0; 0];
ub = [%inf; %inf];
nbVar = 2;
nbCon = 3;
[xopt,fopt,exitflag,output,lambda] = qpipopt(nbVar,nbCon,Q,p,lb,ub,conMatrix,conLB,conUB)

Authors


Report an issue
<< Symphony Toolbox Symphony Toolbox qpipopt_mat >>