lsqnonlin

Parameters

fun :: a function, representing the objective function and gradient (if given) of the problem
x0 :: a vector of double, contains initial guess of variables.
lb :: a vector of double, contains lower bounds of the variables.
ub :: a vector of double, contains upper bounds of the variables.
options :: a list containing the parameters to be set.
xopt :: a vector of double, the computed solution of the optimization problem.
resnorm :: a double, objective value returned as the scalar value i.e. sum(fun(x).^2).
residual :: a vector of double, solution of objective function i.e. fun(x).
exitflag :: The exit status. See below for details.
output :: The structure consist of statistics about the optimization. See below for details.
lambda :: The structure consist of the Lagrange multipliers at the solution of problem. See below for details.
gradient :: a vector of doubles, containing the Objective's gradient of the solution.

Description

Search the minimum of a constrained non-linear least square problem specified by :

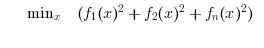
The routine calls fmincon which calls Ipopt for solving the non-linear least square problem, Ipopt is a library written in C++.

The options allows the user to set various parameters of the Optimization problem. It should be defined as type "list" and contains the following fields.

Syntax : options= list("MaxIter", [---], "CpuTime", [---],"GradObj", "on");
MaxIter : a Scalar, containing the Maximum Number of Iteration that the solver should take.
CpuTime : a Scalar, containing the Maximum amount of CPU Time that the solver should take.
GradObj : a string, representing the gradient function is on or off.
Default Values : options = list("MaxIter", [3000], "CpuTime", [600], "GradObj", "off");

The exitflag allows to know the status of the optimization which is given back by Ipopt.

exitflag=0 : Optimal Solution Found
exitflag=1 : Maximum Number of Iterations Exceeded. Output may not be optimal.
exitflag=2 : Maximum CPU Time exceeded. Output may not be optimal.
exitflag=3 : Stop at Tiny Step.
exitflag=4 : Solved To Acceptable Level.
exitflag=5 : Converged to a point of local infeasibility.

For more details on exitflag see the ipopt documentation, go to http://www.coin-or.org/Ipopt/documentation/

The output data structure contains detailed informations about the optimization process. It has type "struct" and contains the following fields.

output.iterations: The number of iterations performed during the search
output.constrviolation: The max-norm of the constraint violation.

The lambda data structure contains the Lagrange multipliers at the end of optimization. In the current version the values are returned only when the the solution is optimal. It has type "struct" and contains the following fields.

lambda.lower: The Lagrange multipliers for the lower bound constraints.
lambda.upper: The Lagrange multipliers for the upper bound constraints.

Examples

//A simple non-linear least square example taken from leastsq default present in scilab
function y=yth(t, x)
y  = x(1)*exp(-x(2)*t)
endfunction
// we have the m measures (ti, yi):
m = 10;
tm = [0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5]';
ym = [0.79, 0.59, 0.47, 0.36, 0.29, 0.23, 0.17, 0.15, 0.12, 0.08]';
// measure weights (here all equal to 1...)
wm = ones(m,1);
// and we want to find the parameters x such that the model fits the given
// data in the least square sense:
//
//  minimize  f(x) = sum_i  wm(i)^2 ( yth(tm(i),x) - ym(i) )^2
// initial parameters guess
x0 = [1.5 ; 0.8];
// in the first examples, we define the function fun and dfun
// in scilab language
function y=myfun(x, tm, ym, wm)
y = wm.*( yth(tm, x) - ym )
endfunction
// the simplest call
[xopt,resnorm,residual,exitflag,output,lambda,gradient] = lsqnonlin(myfun,x0)
// Press ENTER to continue

Examples

//A basic example taken from leastsq default present in scilab with gradient
function y=yth(t, x)
y  = x(1)*exp(-x(2)*t)
endfunction
// we have the m measures (ti, yi):
m = 10;
tm = [0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5]';
ym = [0.79, 0.59, 0.47, 0.36, 0.29, 0.23, 0.17, 0.15, 0.12, 0.08]';
// measure weights (here all equal to 1...)
wm = ones(m,1);
// and we want to find the parameters x such that the model fits the given
// data in the least square sense:
//
//  minimize  f(x) = sum_i  wm(i)^2 ( yth(tm(i),x) - ym(i) )^2
// initial parameters guess
x0 = [1.5 ; 0.8];
// in the first examples, we define the function fun and dfun
// in scilab language
function [y, dy]=myfun(x, tm, ym, wm)
y = wm.*( yth(tm, x) - ym )
v = wm.*exp(-x(2)*tm)
dy = [v , -x(1)*tm.*v]
endfunction
options = list("GradObj", "on")
[xopt,resnorm,residual,exitflag,output,lambda,gradient] = lsqnonlin(myfun,x0,[],[],options)

Report an issue
<< lsqlin	FOSSEE Optimization Toolbox	lsqnonneg >>

lsqnonlin

Calling Sequence

Parameters

Description

Examples

Examples

Authors