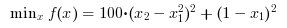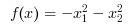<html><head>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8">
<title>fminunc</title>
<style type="text/css" media="all">
@import url("scilab_code.css");
@import url("xml_code.css");
@import url("c_code.css");
@import url("style.css");
</style>
</head>
<body>
<div class="manualnavbar">
<table width="100%"><tr>
<td width="30%">
<span class="previous"><a href="fminimax.html"><< fminimax</a></span>
</td>
<td width="40%" class="center">
<span class="top"><a href="section_44e1f57c5225357b5fe53cb5fad967e9.html">FOSSEE Optimization Toolbox</a></span>
</td>
<td width="30%" class="next">
<span class="next"><a href="intfminbnd.html">intfminbnd >></a></span>
</td>
</tr></table>
<hr />
</div>
<span class="path"><a href="index.html">FOSSEE Optimization Toolbox</a> >> <a href="section_44e1f57c5225357b5fe53cb5fad967e9.html">FOSSEE Optimization Toolbox</a> > fminunc</span>
<br /><br />
<div class="refnamediv"><h1 class="refname">fminunc</h1>
<p class="refpurpose">Solves a multi-variable unconstrainted optimization problem</p></div>
<div class="refsynopsisdiv"><h3 class="title">Calling Sequence</h3>
<div class="synopsis"><pre><span class="default">xopt</span><span class="default"> = </span><span class="functionid">fminunc</span><span class="default">(</span><span class="default">f</span><span class="default">,</span><span class="default">x0</span><span class="default">)</span>
<span class="default">xopt</span><span class="default"> = </span><span class="functionid">fminunc</span><span class="default">(</span><span class="default">f</span><span class="default">,</span><span class="default">x0</span><span class="default">,</span><span class="default">options</span><span class="default">)</span>
<span class="default">[</span><span class="default">xopt</span><span class="default">,</span><span class="default">fopt</span><span class="default">] = </span><span class="functionid">fminunc</span><span class="default">(.....)</span>
<span class="default">[</span><span class="default">xopt</span><span class="default">,</span><span class="default">fopt</span><span class="default">,</span><span class="default">exitflag</span><span class="default">]= </span><span class="functionid">fminunc</span><span class="default">(.....)</span>
<span class="default">[</span><span class="default">xopt</span><span class="default">,</span><span class="default">fopt</span><span class="default">,</span><span class="default">exitflag</span><span class="default">,</span><span class="default">output</span><span class="default">]= </span><span class="functionid">fminunc</span><span class="default">(.....)</span>
<span class="default">[</span><span class="default">xopt</span><span class="default">,</span><span class="default">fopt</span><span class="default">,</span><span class="default">exitflag</span><span class="default">,</span><span class="default">output</span><span class="default">,</span><span class="default">gradient</span><span class="default">]=</span><span class="functionid">fminunc</span><span class="default">(.....)</span>
<span class="default">[</span><span class="default">xopt</span><span class="default">,</span><span class="default">fopt</span><span class="default">,</span><span class="default">exitflag</span><span class="default">,</span><span class="default">output</span><span class="default">,</span><span class="default">gradient</span><span class="default">,</span><span class="default">hessian</span><span class="default">]=</span><span class="functionid">fminunc</span><span class="default">(.....)</span></pre></div></div>
<div class="refsection"><h3 class="title">Input Parameters</h3>
<dl><dt><span class="term">f :</span>
<dd><p class="para">A function, representing the objective function of the problem.</p></dd></dt>
<dt><span class="term">x0 :</span>
<dd><p class="para">A vector of doubles, containing the starting values of variables of size (1 X n) or (n X 1) where 'n' is the number of Variables.</p></dd></dt>
<dt><span class="term">options :</span>
<dd><p class="para">A list, containing the options for user to specify. See below for details.</p></dd></dt></dl></div>
<div class="refsection"><h3 class="title">Outputs</h3>
<dl><dt><span class="term">xopt :</span>
<dd><p class="para">A vector of doubles, containing the computed solution of the optimization problem.</p></dd></dt>
<dt><span class="term">fopt :</span>
<dd><p class="para">A double, containing the the function value at x.</p></dd></dt>
<dt><span class="term">exitflag :</span>
<dd><p class="para">An integer, containing the flag which denotes the reason for termination of algorithm. See below for details.</p></dd></dt>
<dt><span class="term">output :</span>
<dd><p class="para">A structure, containing the information about the optimization. See below for details.</p></dd></dt>
<dt><span class="term">gradient :</span>
<dd><p class="para">A vector of doubles, containing the objective's gradient of the solution.</p></dd></dt>
<dt><span class="term">hessian :</span>
<dd><p class="para">A matrix of doubles, containing the lagrangian's hessian of the solution.</p></dd></dt></dl></div>
<div class="refsection"><h3 class="title">Description</h3>
<p class="para">Search the minimum of an unconstrained optimization problem specified by :</p>
<p class="para">Find the minimum of f(x) such that</p>
<p class="para"><span><img src='./_LaTeX_fminunc.xml_1.png' style='position:relative;top:9px;width:115px;height:26px'/></span></p>
<p class="para">Fminunc calls Ipopt which is an optimization library written in C++, to solve the unconstrained optimization problem.</p>
<p class="para"><h3 class="title">Options</h3>
The options allow the user to set various parameters of the optimization problem. The syntax for the options is given by:</p>
<p class="para">options= list("MaxIter", [---], "CpuTime", [---], "GradObj", ---, "Hessian", ---, "GradCon", ---);</p>
<p class="para"><ul class="itemizedlist"><li>MaxIter : A Scalar, specifying the Maximum Number of Iterations that the solver should take.</li>
<li>CpuTime : A Scalar, specifying the Maximum amount of CPU Time in seconds that the solver should take.</li>
<li>Gradient: A function, representing the gradient function of the objective in Vector Form.</li>
<li>Hessian : A function, representing the hessian function of the lagrange in the form of a Symmetric Matrix with input parameters as x, objective factor and lambda. Refer to Example 5 for definition of lagrangian hessian function.</li></ul>
The default values for the various items are given as:</p>
<p class="para">options = list("MaxIter", [3000], "CpuTime", [600]);</p>
<p class="para">The exitflag allows the user to know the status of the optimization which is returned by Ipopt. The values it can take and what they indicate is described below:
<ul class="itemizedlist"><li>0 : Optimal Solution Found</li>
<li>1 : Maximum Number of Iterations Exceeded. Output may not be optimal.</li>
<li>2 : Maximum amount of CPU Time exceeded. Output may not be optimal.</li>
<li>3 : Stop at Tiny Step.</li>
<li>4 : Solved To Acceptable Level.</li>
<li>5 : Converged to a point of local infeasibility.</li></ul></p>
<p class="para">For more details on exitflag, see the Ipopt documentation which can be found on http://www.coin-or.org/Ipopt/documentation/</p>
<p class="para">The output data structure contains detailed information about the optimization process.
It is of type "struct" and contains the following fields.
<ul class="itemizedlist"><li>output.Iterations: The number of iterations performed.</li>
<li>output.Cpu_Time : The total cpu-time taken.</li>
<li>output.Objective_Evaluation: The number of objective evaluations performed.</li>
<li>output.Dual_Infeasibility : The Dual Infeasiblity of the final soution.</li>
<li>output.Message: The output message for the problem.</li></ul></p>
<p class="para"></p></div>
<p class="para">A few examples displaying the various functionalities of fminunc have been provided below. You will find a series of problems and the appropriate code snippets to solve them.</p>
<div class="refsection"><h3 class="title">Example</h3>
<p class="para">We begin with the minimization of a simple non-linear function.</p>
<p class="para">Find x in R^2 such that it minimizes:</p>
<p class="para"><span><img src='./_LaTeX_fminunc.xml_2.png' style='position:relative;top:10px;width:160px;height:28px'/></span></p>
<p class="para"></p>
<div class="programlisting"><table border="0" width="100%"><tr><td width="98%"><pre class="scilabcode"><span class="scilabcomment">//Example 1: Simple non-linear function.</span>
<span class="scilabcomment">//Objective function to be minimised</span>
<span class="scilabfkeyword">function</span> <span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span><span class="scilabfunctionid">f</span><span class="scilabopenclose">(</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">)</span>
<span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span> <span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">2</span> <span class="scilaboperator">+</span> <span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">2</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">2</span><span class="scilabdefault">;</span>
<span class="scilabfkeyword">endfunction</span>
<span class="scilabcomment">//Starting point</span>
<span class="scilabid">x0</span><span class="scilaboperator">=</span><span class="scilabopenclose">[</span><span class="scilabnumber">2</span><span class="scilabdefault">,</span><span class="scilabnumber">1</span><span class="scilabopenclose">]</span><span class="scilabdefault">;</span>
<span class="scilabcomment">//Calling Ipopt</span>
<span class="scilabopenclose">[</span><span class="scilabid">xopt</span><span class="scilabdefault">,</span><span class="scilabid">fopt</span><span class="scilabopenclose">]</span><span class="scilaboperator">=</span><span class="scilabid">fminunc</span><span class="scilabopenclose">(</span><span class="scilabfunctionid">f</span><span class="scilabdefault">,</span><span class="scilabid">x0</span><span class="scilabopenclose">)</span>
<span class="scilabcomment">// Press ENTER to continue</span></pre></td><td valign="top"><a href="scilab://scilab.execexample/"><img src="ScilabExecute.png" border="0"/></a></td><td valign="top"><a href="scilab://scilab.editexample/"><img src="ScilabEdit.png" border="0"/></a></td><td></td></tr></table></div></div>
<div class="refsection"><h3 class="title">Example</h3>
<p class="para">We now look at the Rosenbrock function, a non-convex performance test problem for optimization routines. We use this example to illustrate how we can enhance the functionality of fminunc by setting input options. We can pre-define the gradient of the objective function and/or the hessian of the lagrange function and thereby improve the speed of computation. This is elaborated on in example 2. We also set solver parameters using the options.</p>
<p class="para"><span><img src='./_LaTeX_fminunc.xml_3.png' style='position:relative;top:10px;width:287px;height:28px'/></span></p>
<p class="para"></p>
<div class="programlisting"><table border="0" width="100%"><tr><td width="98%"><pre class="scilabcode"><span class="scilabcomment">//Example 2: The Rosenbrock function.</span>
<span class="scilabcomment">//Objective function to be minimised</span>
<span class="scilabfkeyword">function</span> <span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span><span class="scilabfunctionid">f</span><span class="scilabopenclose">(</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">)</span>
<span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span> <span class="scilabnumber">100</span><span class="scilaboperator">*</span><span class="scilabopenclose">(</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">2</span><span class="scilabopenclose">)</span> <span class="scilaboperator">-</span> <span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">2</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">2</span> <span class="scilaboperator">+</span> <span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilaboperator">-</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">2</span><span class="scilabdefault">;</span>
<span class="scilabfkeyword">endfunction</span>
<span class="scilabcomment">//Starting point</span>
<span class="scilabid">x0</span><span class="scilaboperator">=</span><span class="scilabopenclose">[</span><span class="scilaboperator">-</span><span class="scilabnumber">1</span><span class="scilabdefault">,</span><span class="scilabnumber">2</span><span class="scilabopenclose">]</span><span class="scilabdefault">;</span>
<span class="scilabcomment">//Gradient of objective function</span>
<span class="scilabfkeyword">function</span> <span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span><span class="scilabfunctionid">fGrad</span><span class="scilabopenclose">(</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">)</span>
<span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span> <span class="scilabopenclose">[</span><span class="scilaboperator">-</span><span class="scilabnumber">400</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">2</span><span class="scilabopenclose">)</span> <span class="scilaboperator">+</span> <span class="scilabnumber">400</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">3</span> <span class="scilaboperator">+</span> <span class="scilabnumber">2</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilaboperator">-</span><span class="scilabnumber">2</span><span class="scilabdefault">,</span> <span class="scilabnumber">200</span><span class="scilaboperator">*</span><span class="scilabopenclose">(</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">2</span><span class="scilabopenclose">)</span><span class="scilaboperator">-</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">2</span><span class="scilabopenclose">)</span><span class="scilabopenclose">]</span><span class="scilabdefault">;</span>
<span class="scilabfkeyword">endfunction</span>
<span class="scilabcomment">//Hessian of Objective Function</span>
<span class="scilabfkeyword">function</span> <span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span><span class="scilabfunctionid">fHess</span><span class="scilabopenclose">(</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">)</span>
<span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span> <span class="scilabopenclose">[</span><span class="scilabnumber">1200</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">2</span><span class="scilaboperator">-</span> <span class="scilabnumber">400</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">2</span><span class="scilabopenclose">)</span> <span class="scilaboperator">+</span> <span class="scilabnumber">2</span><span class="scilabdefault">,</span> <span class="scilaboperator">-</span><span class="scilabnumber">400</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilabdefault">;</span><span class="scilaboperator">-</span><span class="scilabnumber">400</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilabdefault">,</span> <span class="scilabnumber">200</span> <span class="scilabopenclose">]</span><span class="scilabdefault">;</span>
<span class="scilabfkeyword">endfunction</span>
<span class="scilabcomment">//Options</span>
<span class="scilabid">options</span><span class="scilaboperator">=</span><a class="scilabcommand" href="scilab://list">list</a><span class="scilabopenclose">(</span><span class="scilabstring">"</span><span class="scilabstring">MaxIter</span><span class="scilabstring">"</span><span class="scilabdefault">,</span> <span class="scilabopenclose">[</span><span class="scilabnumber">1500</span><span class="scilabopenclose">]</span><span class="scilabdefault">,</span> <span class="scilabstring">"</span><span class="scilabstring">CpuTime</span><span class="scilabstring">"</span><span class="scilabdefault">,</span> <span class="scilabopenclose">[</span><span class="scilabnumber">500</span><span class="scilabopenclose">]</span><span class="scilabdefault">,</span> <span class="scilabstring">"</span><span class="scilabstring">GradObj</span><span class="scilabstring">"</span><span class="scilabdefault">,</span> <span class="scilabfunctionid">fGrad</span><span class="scilabdefault">,</span> <span class="scilabstring">"</span><span class="scilabstring">Hessian</span><span class="scilabstring">"</span><span class="scilabdefault">,</span> <span class="scilabfunctionid">fHess</span><span class="scilabopenclose">)</span><span class="scilabdefault">;</span>
<span class="scilabcomment">//Calling Ipopt</span>
<span class="scilabopenclose">[</span><span class="scilabid">xopt</span><span class="scilabdefault">,</span><span class="scilabid">fopt</span><span class="scilabdefault">,</span><span class="scilabid">exitflag</span><span class="scilabdefault">,</span><span class="scilabid">output</span><span class="scilabdefault">,</span><span class="scilabid">gradient</span><span class="scilabdefault">,</span><span class="scilabid">hessian</span><span class="scilabopenclose">]</span><span class="scilaboperator">=</span><span class="scilabid">fminunc</span><span class="scilabopenclose">(</span><span class="scilabfunctionid">f</span><span class="scilabdefault">,</span><span class="scilabid">x0</span><span class="scilabdefault">,</span><span class="scilabid">options</span><span class="scilabopenclose">)</span>
<span class="scilabcomment">// Press ENTER to continue</span></pre></td><td valign="top"><a href="scilab://scilab.execexample/"><img src="ScilabExecute.png" border="0"/></a></td><td valign="top"><a href="scilab://scilab.editexample/"><img src="ScilabEdit.png" border="0"/></a></td><td></td></tr></table></div></div>
<div class="refsection"><h3 class="title">Example</h3>
<p class="para">Unbounded Problems: Find x in R^2 such that it minimizes:</p>
<p class="para"><span><img src='./_LaTeX_fminunc.xml_4.png' style='position:relative;top:10px;width:134px;height:28px'/></span></p>
<p class="para"></p>
<div class="programlisting"><table border="0" width="100%"><tr><td width="98%"><pre class="scilabcode"><span class="scilabcomment">//Example 3: Unbounded objective function.</span>
<span class="scilabcomment">//Objective function to be minimised</span>
<span class="scilabfkeyword">function</span> <span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span><span class="scilabfunctionid">f</span><span class="scilabopenclose">(</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">)</span>
<span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span> <span class="scilaboperator">-</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">2</span> <span class="scilaboperator">-</span> <span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">2</span><span class="scilabopenclose">)</span><span class="scilaboperator">^</span><span class="scilabnumber">2</span><span class="scilabdefault">;</span>
<span class="scilabfkeyword">endfunction</span>
<span class="scilabcomment">//Starting point</span>
<span class="scilabid">x0</span><span class="scilaboperator">=</span><span class="scilabopenclose">[</span><span class="scilabnumber">2</span><span class="scilabdefault">,</span><span class="scilabnumber">1</span><span class="scilabopenclose">]</span><span class="scilabdefault">;</span>
<span class="scilabcomment">//Gradient of objective function</span>
<span class="scilabfkeyword">function</span> <span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span><span class="scilabfunctionid">fGrad</span><span class="scilabopenclose">(</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">)</span>
<span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span> <span class="scilabopenclose">[</span><span class="scilaboperator">-</span><span class="scilabnumber">2</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">1</span><span class="scilabopenclose">)</span><span class="scilabdefault">,</span><span class="scilaboperator">-</span><span class="scilabnumber">2</span><span class="scilaboperator">*</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">(</span><span class="scilabnumber">2</span><span class="scilabopenclose">)</span><span class="scilabopenclose">]</span><span class="scilabdefault">;</span>
<span class="scilabfkeyword">endfunction</span>
<span class="scilabcomment">//Hessian of Objective Function</span>
<span class="scilabfkeyword">function</span> <span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span><span class="scilabfunctionid">fHess</span><span class="scilabopenclose">(</span><span class="scilabinputoutputargs">x</span><span class="scilabopenclose">)</span>
<span class="scilabinputoutputargs">y</span><span class="scilaboperator">=</span> <span class="scilabopenclose">[</span><span class="scilaboperator">-</span><span class="scilabnumber">2</span><span class="scilabdefault">,</span><span class="scilabnumber">0</span><span class="scilabdefault">;</span><span class="scilabnumber">0</span><span class="scilabdefault">,</span><span class="scilaboperator">-</span><span class="scilabnumber">2</span><span class="scilabopenclose">]</span><span class="scilabdefault">;</span>
<span class="scilabfkeyword">endfunction</span>
<span class="scilabcomment">//Options</span>
<span class="scilabid">options</span><span class="scilaboperator">=</span><a class="scilabcommand" href="scilab://list">list</a><span class="scilabopenclose">(</span><span class="scilabstring">"</span><span class="scilabstring">MaxIter</span><span class="scilabstring">"</span><span class="scilabdefault">,</span> <span class="scilabopenclose">[</span><span class="scilabnumber">1500</span><span class="scilabopenclose">]</span><span class="scilabdefault">,</span> <span class="scilabstring">"</span><span class="scilabstring">CpuTime</span><span class="scilabstring">"</span><span class="scilabdefault">,</span> <span class="scilabopenclose">[</span><span class="scilabnumber">500</span><span class="scilabopenclose">]</span><span class="scilabdefault">,</span> <span class="scilabstring">"</span><span class="scilabstring">GradObj</span><span class="scilabstring">"</span><span class="scilabdefault">,</span> <span class="scilabfunctionid">fGrad</span><span class="scilabdefault">,</span> <span class="scilabstring">"</span><span class="scilabstring">Hessian</span><span class="scilabstring">"</span><span class="scilabdefault">,</span> <span class="scilabfunctionid">fHess</span><span class="scilabopenclose">)</span><span class="scilabdefault">;</span>
<span class="scilabcomment">//Calling Ipopt</span>
<span class="scilabopenclose">[</span><span class="scilabid">xopt</span><span class="scilabdefault">,</span><span class="scilabid">fopt</span><span class="scilabdefault">,</span><span class="scilabid">exitflag</span><span class="scilabdefault">,</span><span class="scilabid">output</span><span class="scilabdefault">,</span><span class="scilabid">gradient</span><span class="scilabdefault">,</span><span class="scilabid">hessian</span><span class="scilabopenclose">]</span><span class="scilaboperator">=</span><span class="scilabid">fminunc</span><span class="scilabopenclose">(</span><span class="scilabfunctionid">f</span><span class="scilabdefault">,</span><span class="scilabid">x0</span><span class="scilabdefault">,</span><span class="scilabid">options</span><span class="scilabopenclose">)</span></pre></td><td valign="top"><a href="scilab://scilab.execexample/"><img src="ScilabExecute.png" border="0"/></a></td><td valign="top"><a href="scilab://scilab.editexample/"><img src="ScilabEdit.png" border="0"/></a></td><td></td></tr></table></div></div>
<div class="refsection"><h3 class="title">Authors</h3>
<ul class="itemizedlist"><li class="member">R.Vidyadhar , Vignesh Kannan</li></ul></div>
<br />
<div class="manualnavbar">
<table width="100%">
<tr><td colspan="3" class="next"><a href="http://bugzilla.scilab.org/enter_bug.cgi?product=Scilab%20software&component=Documentation%20pages" class="ulink">Report an issue</a></td></tr>
<tr>
<td width="30%">
<span class="previous"><a href="fminimax.html"><< fminimax</a></span>
</td>
<td width="40%" class="center">
<span class="top"><a href="section_44e1f57c5225357b5fe53cb5fad967e9.html">FOSSEE Optimization Toolbox</a></span>
</td>
<td width="30%" class="next">
<span class="next"><a href="intfminbnd.html">intfminbnd >></a></span>
</td>
</tr></table>
<hr />
</div>
</body>
</html>